2025.7 做题记录

2025.7 做题记录

2025.7.1

P5496 【模板】回文自动机（PAM） 模板

提交记录

P3649 [APIO2014] 回文串 紫

题意

给你一个由小写拉丁字母组成的字符串 \(s\)。我们定义 \(s\) 的一个子串的存在值为这个子串在 \(s\) 中出现的次数乘以这个子串的长度。

对于给你的这个字符串 \(s\)，求所有回文子串中的最大存在值。

题解

在回文自动机上，每加入一个字符，在新节点的 fail 树到根链上加 1，最后每个点被加 1 的次数就是所对回文串的出现次数，树上差分一下就行了。

提交记录

P4287 [SHOI2011] 双倍回文 紫

题意

称两个相同偶回文串拼起来是“双倍回文串”，求给定字符串的最长双倍回文子串。

题解

我是奶龙。

注意到双倍回文串也是回文串，于是枚举本质不同的回文串然后 manacher 检查一下就行了

提交记录

P5555 秩序魔咒 紫

题意

给定两个小写字母字符串 \(S,T\)，求：

1. 两个字符串的最长公共回文子串。

2. 本质不同的最长公共回文子串个数。

题解

我是奶龙。

把 \(S\) 和 \(T\) 拼到一起建立 PAM，中间间隔两个不同且不在字符集中的字符，这样能保证不存在跨过两个串的回文串。

考虑统计回文串出现次数的过程，然后 PAM 新加入节点时，当前节点在 fail 树到根链上的所有回文串都会在这个位置出现一次。

所以直接线段树合并记录 PAM 每个节点的出现位置集合，然后枚举节点，如果这个节点所对回文串在两个串中都有出现，则更新答案。

写完通过后才发现根本不用线段树合并，因为我们无需知道具体出现位置，只关心出现位置在哪个串即可，所以每个点额外维护两个变量表示是否在 \(S,T\) 中出现过，然后递推上去也能做。

我是奶龙。

提交记录

P4762 [CERC2014] Virus synthesis 紫

题意

你有一个空串，每次可以进行以下操作的一种：

• 在开头和末尾添加一个字符
• 将字符串翻转，设原串为 \(S\)，则新串为 \(S+\operatorname{rev}(S)\)。

求将空串变为给定串的操作次数。

字符集为 \(\{A,G,T,C\}\)。

题解

PAM 上 DP。

最后的肯定是先形成了一个回文子串，然后暴力补全剩余部分形成的。

那么假设存在长为 \(len\) 的回文子串 \(T\)，\(T\) 可以由空串 \(k\) 步形成，那么可以用 \(k+n-|T|\) 更新答案。

于是对所有本质不同的回文串 DP，即 PAM 上 DP。

首先可以归纳证明偶回文串最后一步是操作 2 一定不劣。

\(dp_i\) 表示 PAM 节点 \(i\) 所对回文串的最小操作次数。

则可以左右各去掉一个字符，在翻转前的一侧加上，\(dp_{i}+1\to dp_{ch_{i,A/G/T/C}}\)，不难发现这个转移覆盖了以下情况：

• 上一次翻转操作前，新加入的字符是本串的头或尾。

然后要把没有覆盖到的补上。

考虑上上次翻转操作，如果要做到不在头或尾新加入字符，那么上上次翻转操作形成的串一定是本串的前后缀，由于是回文串，这里只考虑后缀。

假设 \(j\) 节点是 \(i\) 节点的一个回文后缀，且 \(len_j\times 2\leq len_i\)，则 \(dp_{j}+\frac{len_i}{2}-len_j\to dp_{i}\)。

然后发现，如果 \(j\) 不是小于 \(\frac{len_i}{2}\) 的最大回文后缀，那么在添加字符的过程中，会导致最大回文后缀的最后一步不是翻转，与引理 1 矛盾。

于是只转移满足条件的最大的 \(j\) 即可。

注意也可以不做操作二，此时答案为 \(n\)，所以实现时 ans 不能赋极大值，应该赋值为 \(n\)。

提交记录

2025.7.2

CF932G Palindrome Partition *2900

题意

将字符串划分为 \(k\) 个子串，使得第 \(i\) 个子串等于第 \(k-i+1\) 个子串。

求方案数

题解

发现这个东西很像回文串，把两个相等的子串的其中一个反转后穿插到另一个里面，会形成一个偶回文串。

例如两个 \(abcde\) 变成 \(a(e)b(d)c(c)d(b)e(a)=aebdccdbea\)。

那么构造字符串 \(t=s_{1}s_{n}s_{2}s_{n-1}\dots s_{\frac{n}{2}}s_{\frac{n}{2}+1}\)，然后统计 \(t\) 的偶回文划分计数即可。

提交记录

P3501 [POI 2010] ANT-Antisymmetry 蓝

题意

对于一个 \(0/1\) 字符串，如果将这个字符串 \(0\) 和 \(1\) 取反后，再将整个串反过来和原串一样，就称作「反对称」字符串。比如 \(00001111\) 和 \(010101\) 就是反对称的，而 \(1001\) 就不是。
现在给出一个长度为 \(n\) 的 \(0/1\) 字符串，求它有多少个子串是反对称的，注意这里相同的子串出现在不同的位置会被重复计算。

题解

manacher 的正确性依赖回文串的以下两个性质：

1. 若 \([l,r]\) 回文且 \(l+1\leq r-1\)，则 \([l+1,r-1]\) 回文。
2. 若 \([l,r],[a,b]\) 回文且 \(l\leq a\leq b\leq r\)，则 \([l+r-b,l+r-a]\) 回文。

反对称串满足以上两条性质，因此直接 manacher 即可。

注意反对称串长度必须是偶数，最后统计答案要特判。

提交记录

P9646 [SNCPC2019] Paper-cutting 紫

题意

你会得到一张大小为 \(n \times m\) 的纸， 它被划分为 \(n \times m\) 个大小为 \(1 \times 1\) 的块在。这张纸可以按以下方式折叠：

• 可以在两列之间选择一条垂直线，也可以在两行之间选择一条水平线。这条线把纸分成两面。

• 你用这条线作为对称轴，把小的一面折到大的一面上。如果纸的两面大小相等，从两边对折。

你想用这张纸做一幅剪纸杰作。首先，使用上述方法将纸张折叠几次（包括零次）。然后你用剪刀剪纸。每次剪切时，都可以从折叠的纸上剪切出一个连接的部分（即使从外面无法接触到该部分并将其扔掉。请注意，如果两个 $ 1\times 1$ 的块共享一条边，则它们是连接的。

纸张的最终外观是一个包含 \(0\) 和 \(1\) 的大小为 \(n \times m\) 的矩阵，你想知道需要使用剪刀时的最小裁剪次数。

题解

肯定是先横着翻转再竖着翻转，肯定是最后大小越小越好，证明略。

引理 1 对于一个 \(1\times x\) 的串 \(S\)，肯定是先翻转长度最小的偶回文后缀。

证明 假设 \([a,x]\)，\([b,x]\) 都是 \(S\) 的偶回文后缀，且 \(a<b\)，那么可以通过先翻转 \([b,x]\) 再翻转 \([a+\frac{x-b}{2},x-\frac{x-b}{2}]\) 达到翻转 \([a,x]\) 的效果。

同时可以在串两侧加入 \(\inf\) 个万能字符说明左侧和右侧翻折互不影响。

横着翻转和竖着翻转本质相同，只考虑横着翻转，此时行之间独立，因此每次找最大的 \(i\) 满足 \([i,m]\) 在每行都是回文后缀，然后翻转。

最多有 \(m\) 个不同的 \(i\)，每次检查对每个串使用 manacher，复杂度 \(O(行数)=O(n)\)，因此最后复杂度 \(O(nm)\)。

提交记录

2025.7.3

P5410 【模板】扩展 KMP/exKMP（Z 函数） 模板

提交记录

CF126B. Password *1700

题意

找出最长 border 满足其在字符串中出现次数大于等于 \(3\)。

题解

求出 Z 函数，枚举 border 然后用 Z 函数检查中间是否有出现即可。

提交记录

CF432D. Prefixes and Suffixes *2000

题意

求每个 border 的出现次数。

题解

使用 Z 函数，如果 \(z_i>border_x\) 就说明 \(i\) 位置出现了这个 border。

前缀和维护即可。

提交记录

2025.7.4 ~ 2025.7.5

咕咕咕。

2025.7.6

[The 2nd Universal Cup Finals L](Not Another Constructive Problem) *????

题意

给定一个无向图 \(G\)，包含 \(n\) 个顶点，顶点 \(i\) 和 \(j\) 之间有 \(c_{i,j}\) 条无向边（允许多重边）。每个顶点 \(i\) 初始有一个排列值 \(p_i\)（\(1\) 到 \(n\) 的排列），目标是通过特定操作将 \(p_i\) 转换为另一个排列 \(q_i\)。

定义生成树 \(T\) 是 yummy 的，如果存在以下操作序列：

1. 每次选择 \(T\) 中的一条边 \(e = (x, y)\)，交换 \(p_x\) 和 \(p_y\) 的值，并删除 \(e\)。
2. 经过 \(n-1\) 次操作后，所有顶点的值恰好变为目标排列 \(q\)。

任务是统计图 \(G\) 中所有 yummy 生成树的数量，结果对 \(10^9 + 7\) 取模。两个生成树不同当且仅当边集不同。

题解

对节点重标号，使得 \(p_i=i\)，之后考虑置换环。

初始时 \(p_i=i\)，每个节点自成一个环。

每次操作两个属于不同置换环的点，相当于合并两个环。由于是按照树边操作，所以同一个节点不可能被合并两次。说人话就是每次合并都会恰好合并两个环。

那么 \(n-1\) 次操作后就只有一个置换环了，所以如果 \(\{p\}\to \{q\}\) 有多余的置换环，则无解。

然后考虑倒着操作，分裂置换环，发现操作在置换环上不能交叉。同时，如果满足所有操作（即树上的边）在操作环上不交叉，则容易证明可以构造出一种方案。

然后再次根据置换环顺序重标号，问题为对【所有边要么包含要么不交】的树进行计数。

区间 DP，令 \(f_{l,r}\) 表示区间 \([l,r]\) 构成满足条件的树的方案数，令 \(g_{l,r}\) 表示区间 \([l,r]\) 【满足条件 A】的方案数，最终答案为 \(f_{1,n}\)。

条件 A 为：

1. 构成两个连通块，每个连通块都是一个满足条件的树。
2. 连通块内的编号是连续的。

初始时 \(f_{x,x}=1,g_{x,x}=0\)。

转移时，枚举 \(l\) 向后连接的最后一条边，有 \(f_{l,r}=\sum\limits_{k=l}^{r} c_{l,k}\times g_{l,k}\times f_{k,r}\)，\(g_{l,r}=f_{l+1,r}+\sum\limits_{k=l}^{r} c_{l,k}\times g_{l,k}\times g_{k,r}\)。

时间复杂度 \(O(n^3)\)。

提交记录

2025.7.7

[USACO25JAN] Table Recovery S 蓝

题意

Bessie 有一个 \(N\times N\)（\(1\le N\le 1000\)）的加法表，其中对于所有 \(1\le r,c\le N\)，第 \(r\) 行第 \(c\) 列的方格中的整数为 \(r+c\)。

不幸的是，Elsie 得到了这张表格，并通过执行若干次以下三种类型的操作对表格进行了变换。

1. 交换两行；
2. 交换两列；
3. 选择两个同时存在于表格中的值 \(a\) 和 \(b\)，然后同时将每一个 \(a\) 更改为 \(b\)，每一个 \(b\) 更改为 \(a\)。

Elsie 总是按类型顺序执行操作；也就是说，她首先执行任意数量（可能为零）的类型 \(1\) 操作，然后是类型 \(2\) 操作，最后是类型 \(3\) 操作。

请帮助 Bessie 恢复 Elsie 在执行完所有类型 \(1\) 和 \(2\) 操作后，但在执行任意类型 \(3\) 操作之前，表格的一种可能状态。可能存在多种可能的答案，在这种情况下你应当输出字典序最小的答案。

题解

考虑出现一次的数的所对行一定是 \(2\sim n+1\) 或 \(n+1\times 2n\)。

如果已经知道了【这个数的出现次数】和【这个数是否大于等于 \(n+1\)】两个条件，那么这个数唯一确定。

因此讨论出现两次的数，哪个是 \(2\)，一共有两种情况，这两个数确定后根据上面的性质遍历这两个数所在的行，可以唯一确定每个数原来是什么。也就是说最后只有两种情况，比较这两种情况的字典序，然后输出较小的即可。

提交记录

[USACO25FEB] The Best Lineup S 绿

题意

FJ 将以以下方式构造另一条队伍 \(b\)：

• 初始时，\(b\) 为空。
• 当 \(a\) 非空时，移除 \(a\) 最前面的奶牛，并选择是否将该奶牛添加到 \(b\) 的最后。

在 FJ 构造队伍 \(b\) 之前，他可以执行以下操作至多一次：

• 选择队伍 \(a\) 中的一头奶牛，并将其移动至当前位置之前的任意位置。

求他可以达到的字典序最大的 \(b\) 的编号序列。

题解

考虑如果不进行交换，直接取【等于后缀最大值】的数字形成 \(b\) 是最优的。

然后考虑一个位置的后缀最大值和后缀次大值，理想情况一定是先最大后次大。

所以从前往后枚举，找到第一个【后缀次大值在后缀最大值后面】的位置，把次大值交换到最大值前面即可。

提交记录

CF2066D1. Club of Young Aircraft Builders (easy version) *2400

题意

对满足以下条件的长度为 \(m\) 的序列 \(a\) 计数：

• \(a_i\in [1,n]\)。
• 值为 \(n\) 的数恰好出现了 \(c\) 次，且对于任意 \(i\)，\(\sum\limits_{j=1}^{i}[a_j\geq a_i]\leq c\)。

题解

考虑从大到小填数，填到 \(i\) 时，假设已经填了 \(x\) 个比 \(i\) 大的数字，那么可以分析证明 \(i\) 填完之后的位置必须 \(\leq c\)，同时容易证明这个条件是充要的。

因此令 \(f_{i,j}\) 表示只考虑高 \(i\) 层楼，填写 \(j\) 个数的方案数。

有 \(f_{i,j}\times \binom{c}{k}\to f_{i+1,j+k}\)。

提交记录

CF2066D2. Club of Young Aircraft Builders (hard version) *2900

题意

对满足以下条件的长度为 \(m\) 的序列 \(a\) 计数：

• \(a_i\in [1,n]\)，某些位置上的数字已经确定。
• 值为 \(n\) 的数恰好出现了 \(c\) 次，且对于任意 \(i\)，\(\sum\limits_{j=1}^{i}[a_j\geq a_i]\leq c\)。

题解

由于某些位置固定，因此 D1 的做法失效了。

考虑 \(1\) 可以填的位置，显然只能填在前 \(c\) 个。

考虑 \(2\) 可以填的位置，由于 \(2\) 前面 \(\geq 2\) 的不能超过 \(c\)，因此 \(2\) 只能填在前 \(c+cnt_1\) 个。

归纳证明 \(x\) 只能填在 \(c+\sum\limits_{i=1}^{x-1} cnt_i\) 个。

然后考虑已经填的位置的贡献，可以 \(O(nm)\) 预处理出前 \(i\) 个已经确定的数中 \(\geq j\) 的数 \(ge_{i,j}\)。

此时发现一个数依赖比它小的数的状态，因此从小到大填数，令 \(f_{i,j}\) 表示

转移 \(f_{i,j}\) 时，\(i+1\) 可以填入的最大位置为 \(pos=\min(j+c,m)\)，通过 \(pos-ge_{pos,i+1}-j\) 算出空余的位置。

有 \(f_{i,j}\times \binom{pos-ge_{pos,i+1}-j}{k-C_{i+1}}\to f_{i+1,j+k}\)，其中 \(C_{x}\) 表示一开始已经确定了多少个 \(x\)。

注意判断一开始确定 \(i+1\) 的最大位置编号 \(\geq j+c\) 的情况，此时不进行转移。

提交记录

2025.7.8

[USACO21JAN] Spaced Out S 绿

题意

给定一个矩阵，你需要选取若干个位置，满足每个 \(2\times 2\) 方格中恰好有两个被选择，求被选择位置权值之和的最大值。

题解

发现如果同时存在【横向两个连续位置都选】和【纵向两个连续位置都选】，则可以推出矛盾。都不选也是同理的。

那么最终结果要么是每行 01 交替，要么是每列 01 交替，且行列之间独立。

因此维护每行、每列的奇数位置之和、偶数位置之和，然后贪心取最大值即可。

提交记录

[USACO22JAN] Counting Haybales P 紫

题意

有一个长为 \(n\) 的数列 \(h\)，若 \(|h_{i+1}-h_{i}|\leq 1\)，可以交换 \(h_i\) 和 \(h_{i+1}\)。

问最后能得到多少种不同的序列。

题解

核心思路：把数列划分为 \(O(1)\) 个集合，满足每个集合顺序固定，然后按这个顺序 DP。

首先可以发现绝对值相差 \(\geq 2\) 的数对顺序不会改变，且由于改变相同数的位置顺序不会形成新的序列，因此默认相同数相对位置不变。

因此奇偶性相同的数字之间顺序不会改变。

按这个顺序 DP，\(dp_{i,j}\) 表示使用原序列前 \(i\) 个奇数和前 \(j\) 个偶数能组成的集合个数。

预处理一个数往前交换，只考虑奇偶性不同的数带来的限制，能交换到的最前位置 \(p\)。

设 \(odd_{x}\) 表示第 \(x\) 个奇数的位置，\(even_{x}\) 表示第 \(x\) 个偶数的位置。转移时，假设新接入一个奇数，当前已经加入了 \(i\) 个奇数、\(j\) 个偶数，那么如果 \(p_{odd_{i+1}}\leq even_{j}+1\)，则进行转移 \(f_{i,j}\to f_{i+1,j}\)。

复杂度 \(O(n^2)\)。

提交记录

2025.7.9

P9479 [NOI2023] 桂花树 黑

题意

小 B 八年前看到的桂花树是一棵 \(n\) 个节点的树 \(T\)，保证 \(T\) 的非根结点的父亲的编号小于自己。给定整数 \(k\)，称一棵 \((n+m)\) 个节点的有根树 \(T^{\prime}\) 是繁荣的，当且仅当以下所有条件满足：

1. 对于任意满足 \(1 \le i,j \le n\) 的 \((i,j)\)，在树 \(T\) 和树 \(T^{\prime}\) 上，节点 \(i\) 和 \(j\) 的最近公共祖先编号相同。
2. 对于任意满足 \(1 \le i,j \le n + m\) 的 \((i,j)\)，在树 \(T^{\prime}\) 上，节点 \(i\) 和 \(j\) 的最近公共祖先编号不超过 \(\max(i,j)+k\)。

注意题目中所有树的节点均从 \(1\) 开始编号，且根结点编号为 \(1\)。\(T^{\prime}\) 不需要满足非根结点的父亲编号小于自己。

小 B 想知道有多少棵 \((n+m)\) 个节点的树是繁荣的，认为两棵树不同当且仅当存在某一个节点在两棵树上的父亲不同。你只输出方案数在模 \((10^9+7)\) 意义下的值。

题解

条件一等价于原树构成新树的一颗虚树。

考虑 \(k=0\) 的情况，条件二相当于每个点和比它小的点求 LCA，所得结果都不超过这个点。

因此考虑从小到大插入点（相当于去掉限制中的 \(\max\)），插入点 \(i\) 时，要么放到一个点下面，要么插到一条边中，设当前树的节点个数为 \(sz\)，一共有 \(2\times sz-1\) 种插入方法。

因此 \(k=0\) 时，答案为 \(\prod\limits_{i=n}^{n+m-1} (2i-1)\)。

考虑 \(k\neq 0\) 的一般情况，沿续刚才的思路，从小到达插入点。

此时插入一个点时，除了刚才所述的情况，还可能在一个边上加入一个空白点，然后在空白点下面方当前节点。（如图）

注意这个空白节点的意思并不是最终这里只有一个节点，加入恰好一个空白节点可以帮助我们在进行插入点时不重不漏的构造出每个最终状态。

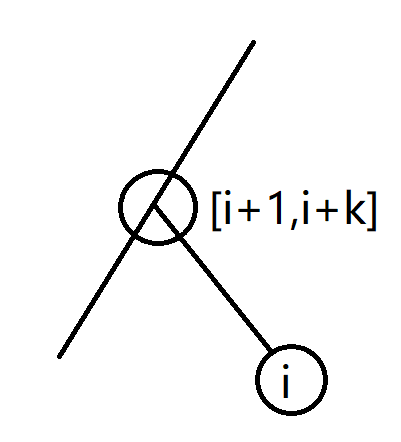
然后考虑状压 DP，\(f_{i,S}\) 表示插入 \(i\) 个点，且前 \(k\) 次操作形成的白点占用情况为 \(S\) 的方案数。

当这次操作没有形成白点或白点已经被占时 \(S\) 这一位为 \(0\)，否则 \(S\) 这一位为 \(1\)。

转移分为三种情况：

• 插到一条边中或挂到一个点下面。
• 在一个边上加入一个空白点，然后在空白点下面方当前节点。
• 填上一个空白点

注意当前树的大小不是 \(i\)，而是 \(i+\operatorname{popcount}(S)\)。

最后答案好像和树的形态没关系（雾）。

提交记录

2025.7.10

P12030 [USACO25OPEN] OohMoo Milk G 紫

题意

给定一个数组，重复以下操作 \(d\) 次：

• 将前 \(A\) 大的数字加 \(1\)。
• 将前 \(B\) 大的数字减 \(1\)。

满足 \(A\geq B\)。

求最终数组的平方和。

题解

首先 \(B\leq A\)，所以操作 2 肯定也只能操作到前 \(A\) 个数字。

显然可以先把前 \(A\) 大中每个数字加上 \(d\)，之后进行 \(d\) 次操作 2。

于是线段树模拟，可以轻松做到 \(O(d\log n)\)。

然后发现问题其实可以转化成重复 \(d\times B\) 次【给最大值减 \(1\)】的操作，但要保证每个数被减的次数不超过 \(d\)。

注意到每个数被减的次数是单调不增的，维护一个极长的相等段，然后尝试和下一段连续段合并，同时维护最小的 \(l\) 满足 \(l\) 被减的次数 \(<d\)。

使用线段树或树状数组实现区间加和单点求和。

提交记录

P12029 [USACO25OPEN] Election Queries G 蓝

题意

维护一个数组，支持：

• 单点修改。
• 查询把数组分成两个集合，每个集合中取一个众数，两个众数之差的最大值。

题解

注意到：

• \(x,y\) 能作为两个集合的众数，当且仅当 \(cnt_x+cnt_y\geq \max\limits_{i=1}^{n} cnt_i\)。
• 不同的 \(cnt\) 只有 \(\sqrt{n}\) 个。

于是随便维护，只要保证每次遍历当前 \(cnt_x\) 不为 \(0\) 的 \(x\)，就能做到 \(O(Q\sqrt{n})\) 的复杂度。

可以使用 set 维护所有的 \(cnt\)，遍历 set 和取出 set 的最值都不带 \(\log\)。

提交记录

[ABC277Ex] Constrained Sums 紫

题意

构造一个长度为 \(n\) 的序列 \(x\)，满足下列条件：

• \(\forall i\in [1,n],\ 0\leq x_i\leq M\)。
• \(\forall i\in [1,Q],\ L_i\leq x_{a_i}+x_{b_i}\leq R_i\)。

题解

2-SAT 在赋值问题上的应用。

定义 \(n\times (m+2)\) 个变量，代表 \([x_i\geq j](1\leq i\leq n,0\leq j\leq m+1)\)。

之后考虑限制条件。

首先对于 \(x_i\geq 0\)，强制其 \(=1\)，即连边 \(\neg (x_i\geq 0)\to (x_i\geq 0)\)；对于 \(x_i\geq m+1\)，强制其 \(=0\)，连边方式同理。

其次若 \(x_i\geq j\)，则有 \(x_i\geq j-1\)；若 \(\neg (x_i\geq j)\) 则有 \(\neg (x_i\geq j+1)\)，连边方式显然。

最后考虑题目限制。

对于限制 \(L_i\leq x_{a_i}+x_{b_i}\leq R_i\)，可转化为如下限制条件：

• \((x_{a_i}\geq j)\to \neg (x_{b_i}\geq R-j+1)\)。
• \(\neg (x_{a_i}\geq j)\to (x_{b_i}\geq L-j+1)\)。

注意 \(a_i,b_i\) 对称，这里省略了两个对称的条件。

建完图跑 2-SAT 即可。

提交记录

2025.7.11

P11844 [USACO25FEB] Friendship Editing G 紫

题意

给定一张 \(N\) 个节点的图，在一次操作中，你可以添加或删除图中的一条边。计算确保以下性质成立所需的最小操作次数：如果存在边 \((a,b)\)，则对于每头其他奶牛 \(c\)，存在边 \((a,c)\) 或者存在边 \((b,c)\)。

\(N\leq 16\)。

题解

妙妙题。

原图不好做，考虑补图，可以归纳证明补图的每个连通块都是完全图。

状压 DP，设 \(dp_{S}\) 表示只考虑集合 \(S\) 的点的最小代价。

每加入一个集合，把集合向外连接的边删掉，之后把集合内没有的边加上。

注意每条修改的边会被两个端点各算一次，因此最终答案要除以 \(2\)。

复杂度 \(O(n^2\times 2^n+3^n)\)。

提交记录

P3209 [HNOI2010] 平面图判定 紫

题意

称可以画在平面上使得任意两条无重合顶点的边不相交的图为平面图。

给定一张 \(N\) 个点 \(M\) 条边的图以及这张图的一个哈密顿回路，判断这张图是否是平面图。

\(N\leq 200,M\leq 10000\)。

题解

将哈密顿回路看成环，一条边要么被画在环内，要么被画在环外。令 \(pos_i\) 表示 \(i\) 在哈密顿回路上的位置编号。

如果两条边 \((a,b),(c,d)\)，满足线段 \([pos_a,pos_b]\) 和 \([pos_c,pos_d]\) 相交，那么 \((a,b)\)，\((c,d)\) 同时画在环内或环外时就会相交。

这相当于 \((a,b)\)，\((c,d)\) 不能同时画在环外或环内，定义 \(M\) 个变量，第 \(i\) 个变量表示第 \(i\) 条边是否画在环内。直接 2-SAT 空间复杂度为 \(O(M^2)\)，无法通过。

引理：去掉重边和自环后，\(M>3\times n-6\) 时无解。

证明：假设一张 \(N\) 个点 \(M\) 条边的图是平面图，那么将图画在平面上，把平面分成 \(F\) 个面。
每条边会恰好计入两个面中，设与面 \(f\) 相邻的面个数为 \(\operatorname{deg}(f)\)，则有 \(\sum\limits_{f} \operatorname{deg}(f)=2\times M\)。
又因为每个面至少由三个边围成，因此 \(\sum\limits_{f} \operatorname{deg}(f)\geq 3\times F\)。
由此可以得出 \(2\times M\geq 3\times F\)，代入欧拉公式 \(N-M+F=2\)，得 \(N-M+\frac{2\times M}{3}\geq 2\)，化简得 \(M\leq 3\times N-6\)。\\ \
因此 \(M>3\times n-6\) 时无解。

提交记录

P5332 [JSOI2019] 精准预测 黑

题意

火星小镇上有 \(n\) 个居民。有 \(m\) 个预测，每个预测都是如下两种形式之一：

1. \(0\ t\ x\ y\)：在 \(t\) 时刻，如果 \(x\) 是死亡状态，那么在 \(t+1\) 时刻，\(y\) 是死亡状态。（注意，当 \(x\) 在 \(t\) 时刻是生存状态时，该预测也被认为是正确的）；
2. \(1\ t\ x\ y\)：在 \(t\) 时刻，如果 \(x\) 是生存状态，那么在 \(t\) 时刻，\(y\) 是死亡状态。（注意，当 \(x\) 在 \(t\) 时刻是死亡状态时，该预测也被认为是正确的）。

注意本题是对某个时刻进行生死状态的预测，如果某个人在 \(t\) 时刻是生存状态，在 \(t+1\) 时刻是死亡状态，你可以认为是在 \(t\) 到 \(t+1\) 这段时间内发生了某个事件导致其死亡。

JYY 希望为每个火星人 \(k\) 计算：

\[\sum_{1 \leq i \leq n,\, i \neq k} \operatorname{Live}(k,i) \]

其中 \(\operatorname{Live}(i,j) = 1\) 表示编号为 \(i\) 和 \(j\) 的火星人有可能同时在第 \(\max\{t\} + 1\) 时刻处于生还状态，否则 \(\operatorname{Live}(i,j) = 0\)。

注意 \(\operatorname{Live}\) 为每一对火星人分别独立计算。火星人是不能够复活的，火星人在任何时候都可能死亡，但任意时刻观察到火星人的状态要么活着，要么死亡。

\(\max\{t\} \leq 10^6\)，\(n \leq 5 \times 10^4\)，\(m \leq 10^5\)。

题解

记 \(T = \max\{t\}\)。

令点 \((i,j)\) 表示 \(i\) 在 \(j\) 时刻活着的状态，\(\neg(i,j)\) 表示 \(i\) 在 \(j\) 时刻死掉的状态。记 \(alive(x) = (x, T+1)\)，\(dead(x) = \neg(x, T+1)\)。

考虑连边方式，和上一题差不多的考虑顺序。基本的限制是：

• 如果 \(i\) 在 \(t\) 活着，那么他在 \(t-1\) 肯定也活着；
• 如果 \(i\) 在 \(t\) 死掉了，那么他在 \(t+1\) 时刻肯定是死掉的。

因此连边：

• \((i,t) \to (i,t-1)\)
• \(\neg(i,t) \to \neg(i,t+1)\)

然后考虑题目要求：

1. 对于 \((0,t,x,y)\)，连边：\(\neg(x,t) \to \neg(y,t+1)\)，\((y,t+1) \to (x,t)\)；

2. 对于 \((1,t,x,y)\)，连边：\((x,t) \to \neg(y,t)\)，\((y,t) \to \neg(x,t)\)。

发现点的个数是 \(O(T\times n)\) 的，爆炸了。

因此考虑省掉一些没有用的点，对于每个人只保留在【题目要求】部分连边被用到的时间，这样点个数就是 \(O(n+m)\) 了。

注意到这是一个 DAG，因为：

• 连接【生】状态之间的边都是 \(t\) 大的指向 \(t\) 小的；
• 连接【死】状态之间的边都是 \(t\) 小的指向 \(t\) 大的；
• 跨越【生】【死】状态的边都是【生】指向【死】的。

所以可以不用缩点。

如果 \(\operatorname{Live}(i,j)=0\)，那么 2-SAT 图缩点后存在一条 \(alive(i) \to dead(j)\) 的边。

不难想到 \(O(n \times (n + m))\) 的暴力：对于每个点 \(p\)，从 \(p\) 开始 DFS，统计搜到的 \(dead(x)\) 个数 \(cnt\)，当 \(alive(p)\) 能到达 \(dead(p)\) 时答案为 \(0\)，否则答案为 \(n - cnt - 1\)。

注意 \(cnt\) 还要算上 \(alive(x)\) 能到达 \(dead(x)\) 这种本来就必死的人。

DAG 上的连通性问题很难继续优化了，因此考虑使用 bitset。

维护 bitset \(f_i\) 表示 \(i\) 能到达的 \(dead\) 集合，反向拓扑一遍即可。

由于空间复杂度 \(O\left(\frac{n \times (n + m)}{w}\right)\) 会炸，考虑时间换空间，把 \(f\) 值域分若干段，每段长度为 \(B\)，然后做 \(\frac{n}{B}\) 次反向拓扑然后拼起来。可以令 \(B = 2 \times 10^4\)。

将反向拓扑改成记忆化搜索实现会简单些。

提交记录

2025.7.12

csp-s模拟测验 T3 赛道设计

题意

构造一个多边形，提供起点的坐标和 \(n\) 个拐点的坐标，坐标必须在 \(0\) 到 \(10^3\)之间，而且起点和所有拐点共 \(n+1\) 个点的坐标不能重复，不允许有线段相交。

给定一个含 L,R 的字符串，对于每个拐点，拐弯方向字符串指定。

题解

考虑有解条件，由于最后要形成闭环，开始可以提供 \(90°,0°,-90°\) 中的任意一个，因此需要满足 \(3\leq |cnt_l-cnt_r|\leq 5\)。

全是 L 或全是 R 是很好构造的。

考虑将原字符串每次删去一个 LR 或 RL，构造出全是 L 或全是 R 的基本图形，再往里面插入 LR 或 RL。

插入时，假设要在 \(pos\) 到 \(pos+1\) 个点插入 LR，记 \(pos\) 到 \(pos+1\) 的方向为 \(drc\)，将 \(pos\) 的 \(drc\) 方向上所有点全部平移 \(1000\) 格，再将 \(pos\) 的 \(L_{drc}\) 方向上所有点全部平移 \(1000\) 格，然后直接插入。

最后对点进行离散化即可。

2025.7.13

P4637 [SHOI2011] 扫雷机器人 紫

题意

在一个直线上排列着 \(n\) 个地雷，第 \(i\) 个地雷的坐标为 \(x_i\)，爆炸威力为 \(d_i\)。若地雷 \(i\) 被引爆，则所有满足 \(|x_i - x_j| \le d_i\) 的地雷 \(j\) 也会被引爆（间接引爆可继续传播）。每次操作从未被引爆的地雷中等概率随机一个地雷进行引爆。求所有地雷都被引爆的期望操作次数。

\(n\leq 4000\)。

题解

若 \(i\) 能引爆 \(j\)，则进行连边 \(i\to j\)，最后形成一张有向图。对有向图进行 SCC 缩点，变成一个 DAG。

原问题转化为 DAG 上的问题，每个点有点权。

发现不能直接 DP，因此考虑推一些性质。

将原问题等价成：进行 \(n\) 次操作，每次随机选择一个未被选择过的点，如果被选择的点没有引爆，引爆它。求实际进行引爆的操作次数的期望。

进一步，这相当于随机一个排列，然后按顺序操作。

拆每个 SCC 的贡献，这个 SCC 被引爆当且仅当【当前 SCC 中的一个点】排到了【所有能到达当前 SCC 的点】的前面。

设第 \(i\) 个 SCC 的大小为 \(sz_i\)，能到达第 \(i\) 个 SCC 的点个数为 \(cnt_i\)（包括第 \(i\) 个 SCC 内部的点），那么上述条件发生在第 \(i\) 个 SCC 的概率为 \(\frac{sz_i}{cnt_i}\)。

这是因为我们可以只考虑能到达第 \(i\) 个 SCC 的点构成的排列，第一个元素确定后，排列的后 \(cnt_i-1\) 项方案数恒为 \((cnt_i-1)!\)，而排列的第一个元素是第 \(i\) 个 SCC 内的元素的概率为 \(\frac{sz_i}{cnt_i}\)。

使用 bitset 维护能到达每个 SCC 的集合。

复杂度为 \(O(\frac{n\times m}{w})=O(\frac{n^3}{2w})\approx 5\times 10^8\) ，实际上边数远远达不到 \(O(n^2)\)，因此可以通过，极限数据用时 \(31\) ms。

提交记录

2025.7.14

CF1361E James and the Chase *3000

题意

给定一张 \(n\) 个点，\(m\) 条有向边的强连通图，如果一个点到其余点都只有恰好一条简单路径，则称这个点是“好点”。

如果“好点”个数不少于 \(0.2\times n\)，则输出所有“好点”，否则输出 -1。

题解

考虑如何判断一个点是否是“好点”，由于给定的图是强连通图，所以从任意一个点 DFS 都能到达所有点，考虑以这个点为根建立 DFS 树，那么这个点是“好点”当且仅当这个 DFS 树不存在前向边和横叉边。

发现一个以“好点”为根的 DFS 树只有返祖边，这是一个很好的性质，因此考虑如何从这颗 DFS 树上得出其他的“好点”。

首先因为 DFS 树没有前向边和横叉边，因此每个点到子树内的点都只有一条简单路径，一个点不是“好点”，当且仅当这个点到子树外某个点有 \(>1\) 条简单路径。

考虑每个点被返祖边覆盖的情况，由于是强连通图，每个点至少被一条返祖边覆盖。

如果一个点被两条及以上返祖边覆盖，那么容易说明，这个点到它的父节点有两条以上的简单路径，因此这个点不是“好点”。

否则，这个点被恰好一条返祖边覆盖，设这个点是 \(x\)，覆盖它的返祖边为 \(u\to v\)。

当 \(v\) 不是“好点”时，说明 \(v\) 到子树外的某个点 \(t\) 有两条简单路径，且这条路径不能经过子树 \(x\)，否则 \(x\) 就被两个返祖边覆盖了。也就是说 \(x\to v\) 的路径拼上 \(v\to t\) 的两条路径都是简单路径，\(x\) 不是“好点”。

当 \(v\) 是“好点”时，说明 \(v\) 所有点都只有一条简单路径，此时有：

• 对于 \(x\) 子树内的点，显然 \(x\) 到这些点只有一条简单路径。
• 对于 \(x\) 子树外的点，\(x\) 到这些点的唯一方法是先到 \(v\)，再从 \(v\) 到这些点，由于 \(v\) 合法，因此 \(x\) 到这些点也只有一条简单路径。

整理一个点是“好点”的条件（不含根节点）：

• 只被一条返祖边覆盖。
• 沿着返祖边走到的点是“好点”。

使用简单的树上 DP 即可求出所有“好点”。

此时还有一个遗留问题，如何找出第一个“好点”？

由于题目只要求“好点”个数大于 \(0.2\times n\) 时才需要输出，因此随机 \(100\) 次，每次选择一个点建树判断，如果随机不出来则输出 -1，复杂度 \(O(n+m)\)，\(100\) 倍常数。

提交记录

P5338 [TJOI2019] 甲苯先生的滚榜 紫

复习平衡树。

提交记录

P4146 序列终结者 紫

复习文艺平衡树。

提交记录

【模板】可持久化平衡树 模板

学习可持久化平衡树。

提交记录

CF1989F Simultaneous Coloring *3000

题意

有一个 \(n\times m\) 的空白矩阵，你可以进行任意次如下操作：

• 花费 \(0\) 代价，将某一行染成红色，或将某一列染成蓝色。该操作会覆盖原先这一 行/列 的颜色。
• 花费 \(k^2\) 代价，同时执行 \(k\) 次操作 1，并任意指定冲突位置（即被超过一个操作覆盖的格子）的颜色。

有 \(q\) 个限制，每个限制形如 \((x,y,c)\)，表示矩阵的 \((x,y)\) 位置必须染成颜色 \(c\)。

对于 \(1\leq i\leq q\) 的每个 \(i\)，计算从空白矩阵开始操作，满足限制 \(1\sim i\) 的最小代价。

\(n,m,q\leq 2\times 10^5\)。

题解

如果要求 \((i,j)\) 是红色，那么说明【对第 \(j\) 列操作】一定在【对第 \(i\) 行操作】之后，对这个限制进行图论建模，连边 \(i\to j\)。 如果要求 \((i,j)\) 是蓝色，那么连边 \(j\to i\)。

考虑如何对单次询问计算答案，SCC 缩点后，同一个 SCC 内显然是矛盾的，需要花费 SCC 大小平方的代价（大小为 \(1\) 的 SCC 代价是 \(0\)）。SCC 之间的图一定是 DAG，按照拓扑序操作即可。

那么我们要做的就是动态加入有向边，查询所有 SCC 大小的平方和减去大小为 \(1\) 的 SCC 个数。

发现如果加入的是无向边，可以直接并查集。考虑动态维护有向图连通性的套路，使用整体二分算出每条边加入 SCC 的时间，之后按照无向边计算。

注意整体二分的时候不应该把边拆成操作和询问，因为动态加边的 SCC 本身是非常难维护的，所以应该把边当成操作和询问合一的东西，然后用并查集把已经加入 SCC 的边缩到一个点中，其余边进入右侧二分结构。之后撤销后再进入左侧二分结构。

具体地，整体二分 solve(ansL,ansR,edges[]) 的流程如下：

全局实时维护可撤销并查集，如果当前二分区间为 \([ansL,ansR]\)，则并查集已经将编号在 \([1,ansL)\) 中的边加入，并把 SCC 缩成了一个点。

• 当 \(ansL=ansR\) 时记录答案并返回。
• 记 \(mid=\frac{ansL+ansR}{2}\)，将出现时间在 \(mid\) 之前的边加入缩好点的图中（即外层并查集维护的图），并对原来缩好点的图再次进行缩点，更新并查集。
• 检查所有出现时间在 \(mid\) 之前的边，将两端点在同一 SCC 内的边拿出来，进入右侧递归。
• 撤销第二步并查集的操作。
• 将剩余的边拿出来，进入左侧递归。

提交记录

2025.7.15

P4315 月下“毛景树” 蓝

复习树链剖分。

提交记录

P3401 洛谷树 紫

题意

给定一棵树，维护两种操作：

• 1 u v，求 \(u\to v\) 的路径中【所有子路径的异或和】的算数和。
• 2 u v w，将边 \((u,v)\) 的权值改成 \(w\)，保证 \((u,v)\) 存在。

题解

虽然可以直接序列做法上树，但是有更巧的做法。

维护 \(a_u\) 表示 \(u\) 到根链的异或和，路径 \(u\to v\) 的异或和可以表示为 \(a_u\operatorname{xor} a_v\)。

拆位，设路径 \(u\to v\) 上的 \(2^w\) 位有 \(cnt1\) 个 \(1\)，\(cnt0\) 个 \(0\)，那么这一位的贡献就是 \(2^w\times cnt1\times cnt0\)。

修改时只需要将到根链翻转，使用树剖维护即可。

提交记录

P3676 小清新数据结构题 紫

题意

给定一棵树，维护两种操作：

• 1 x y，将 \(x\) 的点权改为 \(y\)，即 \(val_x\leftarrow y\)。
• 2 x，以 \(x\) 为根，求所有子树点权和的平方和，即求 \(\sum\limits_{u=1}^{n} (\sum\limits_{v\in \operatorname{subtree}(u)} val_v)^2\)。

\(n\leq 2\times 10^5\)。

题解

对于操作二，保持以 \(1\) 为根，不在 \(x\) 到根链上的点查询的仍然是以 \(1\) 为根的子树 \(x\)，在 \(x\) 到根链上的点查询的是 \(x\) 方向节点的子树补，节点 \(x\) 查询的是全局。

因此分类讨论即可，把序列维护平方和的方法用树链剖分搬到树上。

线段树上维护 \(\sum 1,\sum val,\sum sz,\sum val\times sz,\sum val^2,\sum sz^2\)。

提交记录

P5391 [Cnoi2019] 青染之心 紫

题意

Cirno 初始有一个空的物品序列，一个大小为 \(V\) 的背包，现在你有 \(q\) 个操作，分为两种：

• add x y：表示加入一种体积为 \(x\), 价值为 \(y\) 的物品到序列末尾。
• erase：表示删除序列末尾的物品。

在每个操作结束以后，你需要求出：

假设序列中的每种物品都有无穷多个，Cirno 的背包可以装下的物品最大价值和。

\(q,V\leq 2\times 10^4\)，5s，64MB。

题解

将操作视为一棵树，暴力做，发现时间可以接受，空间接受不了。

树链剖分，每个重链维护一个 DP 数组，在树上 DFS 时需要维护这个点到根链的 DP 数组，因此可以划分为不超过 \(O(\log n)\) 个重链。

维护 \(dp_{lev,x}\) 表示经过 \(lev\) 条重链，重量为 \(x\) 的最大价值。

之后处理加入物品，往下 dfs 即可。

提交记录

P5314 [Ynoi2011] ODT 黑

题意

给你一棵树，边权为 \(1\)，有点权。

需要支持两个操作：

• 1 x y z：表示把树上 \(x\) 到 \(y\) 这条简单路径的所有点点权都加上 \(z\)。
• 2 x y：表示查询与点 \(x\) 距离小于等于 \(1\) 的所有点里面的第 \(y\) 小点权。

题解

考虑每个点维护一颗平衡树表示其子节点构成的集合，直接树剖+树套树是三只 \(\log\) 的，过不去。

考虑让平衡树契合树链剖分的结构，每个点维护一颗平衡树表示其轻儿子构成的集合，这样一次路径修改只需要改 \(O(\log n)\) 个节点的平衡树，总复杂度双 \(\log\)。

提交记录

2025.7.16

P5642 人造情感（emotion） 黑

题意

给你一颗 \(n\) 个节点的树，以及 \(m\) 条路径 \((u, v, w)\)，其中 \(w\) 可以认为是 \((u, v)\) 这题路径被标记的一个权值。一个路径集合 \(S\) 的重量 \(W(S)\) 记为：找出 \(S\) 的一个权值之和最大的子集，该子集满足任何两条路径没有公共点，这个子集的所有路径权值之和就是 \(W(S)\)。

记 \(f(u, v) = w\) 为最小的非负整数 \(w\)，使得对于给定的 \(m\) 条边组成的路径集合 \(U\)，\(W(U \cup \{(u, v, w + 1)\}) > W(U)\) 。

请你计算下式，对 \(998244353\) 取模。

\[\sum_{u=1}^n \sum_{v=1}^n f(u, v) \]

题解

Part1. 求 \(W(S)\)

考虑 DP 先求出 \(W(S)\)。

令 \(f_u\) 表示 \(u\) 子树内，\(u\) 点可用可不用的答案。

令 \(g_u\) 表示 \(u\) 子树内，\(u\) 点必须不用的答案。

令 \(c_u=g_u-f_u\)，表示将 \(u\) 空出来的代价。

考虑转移，把每个路径挂在路径的 lca 上，有：

\[g_x\leftarrow \sum\limits_{y\in son_x} f_y \\ f_x=g_x+\max(0,\max\limits_{\operatorname{lca}(u_j,v_j)=x}\{w_j+\sum\limits_{k\in \operatorname{path}(u_j,v_j)}c_k\}) \\ W(S)=f_1 \]

这部分转移需要支持单点修改，路径查询，将路径差分成到根链，之后转化为子树修改，单点查询，使用树状数组即可。

Part2. 求单个 \(F(i,j)\)

考虑加入一条边 \((u,v,w+1)\) 让独立集变大，那么要求这条边一定被选，仿照 DP 中选一条边的方式，有 \(F(i,j)=-\sum\limits_{k\in \operatorname{path}(i,j)} c_k\)。

当然，这是错的。

因为 \(c_u\) 定义中，【将 \(u\) 空出来的代价】只考虑了子树内的路径，我们还需要考虑子树外的路径，也就是说不存在一个经过 \((fa_{\operatorname{lca}(i,j)},\operatorname{lca}(i,j))\) 的路径被选择。

令 \(h_u\) 表示整棵树空出 \((fa_{u},u)\) 的答案，则空出 \((fa_{u},u)\) 的代价为 \(h_u-f_1\)，有：

\[F(i,j)=-\sum\limits_{k\in \operatorname{path}(i,j)} c_k-(h_{\operatorname{lca}(i,j)}-f_1) \]

Part3. 求 \(h\)

问题在于如何求 \(h\)，初值有 \(h_1=f_1\)，仿照求 \(W(S)\) 中【朴素转移+强制选路径转移】设计 \(h\) 的转移：

\[h_x\leftarrow h_{fa_x}+c_{fa_x} \\ h_x\leftarrow h_{\operatorname{lca}(u,v)}+w+\sum\limits_{k\in \operatorname{path}(u,v)} c_k\ \ \ ((u,v,w)\in S\land x\notin \operatorname{path}(u,v)\land fa_x\in \operatorname{path}(u,v)) \]

对于第二种转移，解释为强制选择路径 \((u,v,w)\)，这样能保证 \((x,fa_x)\) 不被选。

对于第一种转移，解释为强制去掉 \(fa_x\) 子树外经过 \((fa_{fa_x},fa_x)\) 的路径（由 \(h\) 保证）和 \(fa_x\) 子树内经过 \(fa_x\) 的路径（由 \(c\) 保证），如果去掉的路径不经过 \((x,fa_x)\) 也没关系，因为这样一定能被第二种转移覆盖到。

对于第二种转移的优化，考虑给路径上每个点打标记 \((u,x,y,z)\)，表示在节点 \(u\)，值为 \(x\)，不能下传到 \(y,z\)。

下传标记时，将标记从大到小排序遍历，每次只操作没有被下传过的子节点，保证每个点的子节点只被操作一次，这样复杂度是 \(O(标记个数)\) 的。

考虑重链剖分，每条路径上大多数标记都是 \((u,x,\operatorname{heavy\_child}_u,0)\)，其余标记不超过 \(O(\log n)\) 个。

对于 ，维护 \(t_u\) 表示 \(x\) 最大的 \((u,x,\operatorname{heavy\_child}_u,0)\)。\(t_u\) 的修改相当于树的链上取 \(\max\)，直接树剖，其余标记个数为 \(O(n\log n)\)，使用上面 \(O(标记个数)\) 的方法。

Part4. 求所有 \(F(i,j)\)

即求：

\[\sum_{i=1}^{n} \sum_{j=1}^{n} \left(-\sum\limits_{k\in \operatorname{path}(i,j)} c_k-(h_{\operatorname{lca}(i,j)}-f_1)\right) \\ =n^2\times f_1-\sum_{i=1}^{n} \sum_{j=1}^{n} h_{\operatorname{lca}(i,j)}-\sum_{i=1}^{n} \sum_{j=1}^{n} \sum\limits_{k\in \operatorname{path}(i,j)} c_k \\ n^2\times f_1-\sum_{k=1}^{n} \left(h_k\times \sum_{1\leq i,j\leq n\land \operatorname{lca}(i,j)=k} 1\right)-\sum_{k=1}^{n} \left(c_k\times \sum_{1\leq i,j\leq n\land k\in \operatorname{path}(i,j)} 1\right) \]

对于每个点 \(u\)，记有 \(p_u\) 条路径的 lca 是 \(u\)，有 \(q_u\) 条路径经过 \(u\)，则答案为：

\[n^2\times f_1-\sum_{k=1}^{n} p_k\times h_k-\sum_{k=1}^{n} q_k\times c_k \]

\(p,q\) 都是好维护的，至此本题所有问题已解决。

提交记录

2025.7.17

QOJ #5357. 芒果冰加了空气 *????

题意

给定一颗 \(n\) 个节点的树，求对这棵树进行点分治的方案数（不要求分治中心是重心）。

\(n\leq 5000\)。

题解

考虑树上背包合并 \(u,v\) 时，合并两个点分树的过程，为了保证不重不漏，我们要保证 \(u,v\) 所在的点分树是合并后的点分树的虚树。

发现点分树上 \(u\) 不能低于 \(v\) 的儿子，因为删完 \(v\) 后 \(u\) 和 \(v\) 的儿子不连通了。

其次 \(u,v\) 是相邻的，所以 \(u,v\) 在点分树上必须是祖先关系。

然后对于点分树上 \(u\) 的父亲，由于 \(u,v\) 是祖先关系，\(u\) 的父亲和 \(u\) 是祖先关系，所以 \(u\) 的父亲和 \(v\) 是祖先关系。

之后可以归纳证明 \(u\) 在点分树上的到根链与 \(v\) 在点分树上的到根链互相具有祖先关系，即这两条链形成了一条链。

由于 \(u\) 不能低于 \(v\) 的儿子，\(v\) 同理，且 \(u,v\) 所在的点分树是合并后的点分树的虚树，因此我们确实只需要合并 \(u\) 的到根链和 \(v\) 的到根链。

设 \(u,v\) 在点分树上的到根链的节点数（即深度）分别为 \(n,m\)，这相当于合并长度分别为 \(n,m\) 的序列，逆向思考相当于从 \(n+m\) 的最终序列中选 \(n\) 个作为第一个序列，方案数为 \(\binom{n+m}{n}\)。

设 \(f_{u,i}\) 表示只考虑 \(u\) 子树内的信息，\(u\) 到点分树根节点深度为 \(i\) 的方案数。

则有 \(f_{u,i}\times f_{v,j}\times \binom{i-1+j-k}{i-1}\to f_{u,i+j-k}\)，\(O(n^3)\)。

改成填表法的式子 \(f_{u,z}\leftarrow f_{u,x}\times f_{v,y}\times \binom{z-1}{x-1}\ \ \ (x\leq z\leq x+y)\)。

即 \(f_{u,z}\leftarrow f_{u,x}\times \binom{z-1}{x-1}\times \sum\limits_{y=z-x}^{sz_v}f_{v,y}\)，后缀和优化，将 \(x\) 的范围限制在 \([z-sz_v,z]\)，复杂度为树上背包的复杂度，即 \(O(n^2)\)。

注意背包的复杂度不要写假，确保转移复杂度为 \(sz_u\times sz_v\)，而不是 \((sz_u+sz_v)\times sz_v\)。

提交记录

[AGC001C] Shorten Diameter 绿

题意

给你一棵 \(N\) 个点的无向树，你需要删除一些点，使树的直径小于等于 \(K\)，当且仅当删除某点不会对树的联通性产生影响时才可以删除。问至少删除多少点才可以满足要求。

\(n\leq 2000\)，但复杂度可以更优。

题解

设树 \(T\) 的直径为 \(D\)，有如下性质：

• 若 \(D\) 是偶数，则存在某个顶点 \(v\)，使得从 \(v\) 到其他所有顶点的距离都不超过 \(\frac{D}{2}\)。

• 若 \(D\) 是奇数，则存在某条边 \(e\)，使得从 \(e\) 到其他所有顶点的距离都不超过 \(\frac{D-1}{2}\)。

证明的话就是如果两个直径不交，则连接两个直径的端点可以发现一条更长的路径，推出矛盾。

称 \(v\) 或 \(e\) 为树的中心。

枚举删完后树的中心，删去距离大于 \(\frac{k}{2}\) 的点。

因此统计每个点距离大于 \(\frac{k}{2}\) 的点个数，使用点分治，复杂度 \(O(n\log^2 n)\)。

但是 \(O(n^2)\) 就可以过了。

提交记录

QOJ #4815. Flower's Land *????

题意

给你一颗树，点有点权，对于 \(1\leq i\leq n\) 的每个 \(i\)，求满足以下条件的连通块的点权之和最大值：

• 包含点 \(i\)。
• 大小为 \(k\)。

\(n\leq 40000,k\leq 3000\)，8s，2048MB。

题解

发现本题严格不弱于 P6326 Shopping，考虑点分治处理连通块，对于每一层，本质上是要解决这样的问题：

• 选一个包含分治中心且包含点 \(i\) 的连通块，大小为 \(k\)，权值最大化。

考虑按 dfn 转移，以分治中心为根 dfs，如果不选 \(x\)，那么就不能选 \([x,x+sz[x]-1]\) 的所有点。

令 \(f_{i,j}\) 表示 \(dfn\in [1,i)\)，选 \(j\) 个点的答案，\(g_{i,j}\) 表示 \(dfn\in [i,sz[rt]]\)，选 \(j\) 个点的答案。

则有：

\[f_{i+1,j+1}\leftarrow f_{i,j}+a_{Idfn_i} \\ f_{i+sz_{Idfn_i},j}\leftarrow f_{i,j} \\ g_{i,j}\leftarrow g_{i+1,j-1}+a_{Idfn_i} \\ g_{i,j}\leftarrow g_{i+sz_{Idfn_i},j} \]

在更新答案时，为了保证 \(i\) 被选择，需要在转移 \(g\) 的循环内更新答案，在 \(g_i\) 进行第二种转移之前使用 \(f_{i,x}+g_{i,k-x}\) 更新答案，这样 \(g\) 只考虑了 \(i\) 被选择的情况，符合题意。

提交记录

CF2101E. Kia Bakes a Cake *3100

题意

给定一个长度为 \(n\) 的二进制字符串 \(s\) 和一棵包含 \(n\) 个顶点的树 \(T\)。

一个序列 \((v_1, v_2, \ldots, v_m)\) 被称为"优美的"，当且仅当：

• 路径中每个相邻点对的距离必须至少是上一个相邻点对的两倍。
• 路径上的每个点对应的 \(s\) 都为 1。

对于每个 \(1 \le i \le n\land s_i = \mathtt{1}\) 的 \(i\)，求 \(v_1=i\) 的优美序列的最长长度。

题解

真的有 *3100 吗？

注意到答案是 \(O(\log n)\) 级别的，考虑 DP 并把序列长度计入状态，由于还要记起点，倒着 DP，令 \(f_{i,j}\) 表示已经确定序列后 \(j\) 个值，且当前在节点 \(i\)，上一个点到 \(i\) 的距离的最大值。

转移为 \(\operatorname{dist}(i,k)\to f_{k,j+1}\ \ \ (\operatorname{dist}(i,k)\leq \frac{f_{i,j}}{2})\)。

使用点分治优化转移，可以做到 \(O(n\log^3 n)\)。

最后 \(i\) 的答案为满足 \(f_{i,x}\neq 0\) 的最大的 \(x\)。

提交记录

2025.7.18

P2500 [SDOI2012] 集合 紫

题意

给出n个点m条边的带权无向图，有3个集合A、B、C。一开始无向图中所有点都属于A集合，有如下 \(9\) 种操作：

MoveP x：表示将第x个点从所在集合中删除，并加入至 P 集合。（\(P\in \{A,B,C\}\)）

AskPQ：询问两个端点分别属于P集合和Q集合的所有边中最小的权值是多少。（\(P,Q\in \{A,B,C\}\)）

\(n<=100000,m<=500000,q<=100000\)。

题解

维护 \(6\) 个集合 \(s_{P,Q}\) 表示 \(P,Q\) 集合之间的边，然后暴力修改，发现复杂度爆炸了。

于是根据点的度数根号分治。

对于度数小于 \(\leq \sqrt{m}\) 的点按上述暴力，度数大于 \(\sqrt{m}\) 的点最多 \(\sqrt{m}\) 个，对这些点维护三个集合，表示这些点向 \(A,B,C\) 的连边。

每次修改枚举所有度数大于 \(\sqrt{m}\) 的点。最后复杂度 \(O(n\sqrt{m}\log m)\)。

提交记录

P8250 交友问题 蓝

题意

给定一张无向图，每次询问给两个点 \(u,v\)，求【与 \(u\) 距离为 \(1\) 的点】中，满足【与 \(v\) 距离 \(>1\)】的点的个数。

\(n,q\leq 2\times 10^5,m\leq 7\times 10^5\)。

题解

下文中，“\(x\) 的邻域”指距离 \(x\) 恰好为 \(1\) 的点。

根号分治。

• \(deg_u,deg_v\leq B\)
  • 暴力，在 \(v\) 和 \(v\) 的邻域打上标记，暴力枚举 \(u\) 的邻域，计算没有被标记的点个数 \(t\)，答案为 \(t\)。复杂度 \(O(q\times B)\)。
• \(deg_u\geq B\)
  • 不同的 \(u\) 只有 \(\frac{n}{B}\) 个。
  • 询问离线并去重，对于相同的 \(u\)，先在 \(u\) 的邻域打上标记，然后对于每个不同的 \(v\)，暴力枚举邻域，计算被标记的点个数 \(t\)，答案为 \(deg_u-t\)。对于相同的 \(u\)，每个不同的 \(v\) 只会被算一次，总复杂度 \(O(\sum\limits_{i=1}^{n} deg_i)=O(m)\)。
  • 一共有 \(\frac{n}{B}\) 个不同的 \(u\)，这部分总复杂度 \(O(\frac{n\times m}{B})\)。
• \(deg_v\ge B\)
  • 不同的 \(v\) 只有 \(\frac{n}{B}\) 个。
  • 询问离线并去重，对于相同的 \(v\)，先在 \(v\) 和 \(v\) 的邻域打上标记，然后对于每个不同的 \(u\)，暴力枚举邻域，计算没有被标记的点个数 \(t\)，答案为 \(t\)。对于相同的 \(v\)，每个不同的 \(u\) 只会被算一次，总复杂度 \(O(\sum\limits_{i=1}^{n} deg_i)=O(m)\)。

令 \(q\times B=\frac{n\times m}{B}\)，即 \(B=\sqrt{\frac{n\times m}{q}}\)，时间复杂度 \(O(q\sqrt{\frac{n\times m}{q}})\)。

提交记录

CF1270F. Awesome Substrings *2600

题意

给定一个 \(n\) 位二进制字符串，求满足以下条件的子串数量：

• 至少包含 \(1\) 个 \(1\)。
• 长度能被其中 \(1\) 的个数整除。

\(n\leq 2\times 10^5\)。

题解

根号分治。

转化成前缀和，答案为 \(\sum\limits_{k=1}^{n}\sum\limits_{i=1}^n\sum\limits_{j=0}^{i-1} [k\times (s_i-s_j)=i-j]=\sum\limits_{k=1}^{n}\sum\limits_{i=1}^n\sum\limits_{j=0}^{i-1} [k\times s_i-i=k\times s_j-j]\)。

当 \(k\leq \sqrt{n}\) 时暴力枚举 \(k\)，对每个 \(k\) 暴力 \(O(n)\) 计算答案，这部分复杂度位 \(O(n\sqrt{n})\)。

当 \(k>\sqrt{n}\) 时 \(1\) 的个数 \(\leq \sqrt{n}\)，因此枚举左端点和 \(1\) 的个数，确定右端点所在区间，\(O(1)\) 计算答案，这部分复杂度位 \(O(n\sqrt{n})\)。

时间复杂度 \(O(n\sqrt{n})\)。

提交记录

2025.7.19

CF940F. Machine Learning *2600

题意

给你一个数组 \(a_i\)，支持两种操作：

1. 查询区间 \([l, r]\) 中每个数字出现次数的 \(\text{mex}\)。
2. 单点修改某一个位置的值。

\(n, Q \le 10^5\)。

题解

先离散化，然后带修莫队，本质上要维护一个集合，支持插入、删除、求 \(\text{mex}\)。

这看起来必须要带 \(\log\)，但是注意到题目求的是出现次数的 \(\text{mex}\)，而不同的出现次数只有 \(O(\sqrt{n})\) 个，因此对于每个询问暴力求即可。

提交记录

CF852I Dating *2300

题意

给定一颗树，树上节点有黑色和白色之分，点有点权，每次询问一条路径，求路径上颜色不同且点权相同的点对数量。

\(n,q\leq 10^5\)。

题解

学习树上莫队。

简单容斥，相当于 \(\sum cnt^2-\sum\limits_{白点} cnt^2-\sum\limits_{黑点} cnt^2\)。

然后树上莫队即可。

提交记录

P10590 磁力块 紫

题意

有 \(N\) 块磁石，每个磁石的性质可以用一个五元组 \((x,y,m,p,r)\) 描述，其中 \(x,y\) 表示其坐标，\(m\) 是磁石的质量，\(p\) 是磁力，\(r\) 是吸引半径。

若磁石 \(A\) 与磁石 \(B\) 的距离不大于磁石 \(A\) 的吸引半径，并且磁石 \(B\) 的质量不大于磁石 \(A\) 的磁力，那么 \(A\) 可以吸引 \(B\)。

小取酒有一块磁石 \(L\)，坐标为 \((x_0,y_0)\)，他手持磁石 \(L\) 并保持原地不动，所有可以被 \(L\) 吸引的磁石将会被吸引过来。

在每个时刻，他可以选择更换任意一块自己已经获得的磁石，在 \((x_0,y_0)\) 处吸引更多的磁石。

求小取酒最多能获得多少块磁石。

题解

分块优化 BFS。

朴素 BFS 是 \(O(n^2)\) 的。

记一个点到 \((x_0,y_0)\) 的距离为 \(dis\)，考虑我们对点 \(u\) 进行松弛时，实际上需要找出所有 \(dis\leq r_u,m\leq p_u\) 的点，这是一个二位偏序问题。

分块优化，把节点整体按 \(m\) 排序，每个块内再按 \(dis\) 排序，维护一个指针 \(l\) 表示这个块的前 \(l\) 个已经被访问。每次松弛时，找到第一个满足【块内存在一个 \(m\) 大于 \(p_u\)】的块，对于这个块暴力，对于前面的块，\(m\) 一定符合要求，因为对于每个块 \(dis\) 单增，因此每个块都可以通过移动 \(l\) 指针遍历所有满足条件的点。对于前面的每个块都进行移动指针的操作即可。

总复杂度 \(O(n\sqrt{n})\)。

提交记录

CF455D Serega and Fun *2700

题意

给定长度为 \(n (1 \le n \le 10^5)\) 的序列 \((1 \le a_i \le n)\)，共有 \(q (1 \le q \le 10^5)\) 个询问，支持两种操作：

• 1 l r 将区间 \([l, r]\) 依次向右移动一位，其中 \(a_r\) 移动到 \(a_l\)。
• 2 l r k 询问区间 \([l, r]\) 中 \(k\) 出现次数。

强制在线。

题解

一看就不是 \(polylog\) 能解决的东西，考虑分块，每个块维护一个 deque 和一个桶，移动时如果 \(l,r\) 在同一个块就暴力，否则重构 \(l,r\) 所在的两个块，然后中间的每个块的 deque 弹出最后一个元素并将其加入下一个块的第一个元素，实时维护计数桶。查询就是整块查桶、散块暴力。

提交记录

P11527 [THUPC 2025 初赛] waht 先生的法阵 紫

题意

维护一个内向森林，给定序列 \(\{a\}\)，对于每个 \(1\leq i\leq n\) 的 \(i\)，如果 \(i+\gcd(a_i,i)\leq n\)，则 \(i\) 向 \(i+\gcd(a_i,i)\leq n\) 连有向边，你需要支持：

• 给定 \(l,r,c\)，对于 \(l\leq i\leq r\) 的每个 \(i\)，\(a_i\leftarrow a_i\times c\)。
• 给定 \(x\)，求 \(x\) 的到根链节点的 \(a\) 的和，对 \(998244353\) 取模。

\(n\leq 2.5\times 10^5\)，5s。

题解

与 CF1491H Yuezheng Ling and Dynamic Tree 十分相似。

分块，维护 \(f_i\) 表示 \(i\) 的父亲，\(g_i\) 表示 \(i\) 第一次跳出块的节点标号，\(sum_i\) 表示从 \(i\) 开始跳，第一次跳出块前的权值和。

将修改拆为改 \(f\) 和改 \(a\) 两部分。先讨论改 \(f\)，对于一个 \(i\)，\(\gcd(i,a_i)\) 的个数不超过 \(i\) 的质因数个数，\(\gcd(i,a_i)\) 的总共可能出现的数字个数为 \(\sum\limits_{i=1}^{n} \operatorname{Num\_Of\_PrimeDivisers}(i)=O(埃筛复杂度)=O(n\ln \ln n)\)，因此可以均摊修改复杂度，每次进行修改时暴力重构该块。再讨论改 \(a\)，这个是简单的，记 \(tag_i\) 表示第 \(i\) 个块的 \(a\) 的全局乘法懒标记，散块暴力、整块打 \(tag\)。

设块长为 \(B\)，如果能做到均摊，修改的总时间复杂度为 \(O(B\times n\ln \ln n)\)。

查询直接整块往前跳，跳不了就一步步跳，查询的总时间复杂度为 \(O(m\times \frac{n}{B})\)。

令 \(B\times n\ln \ln n=m\times \frac{n}{B}\)，即 \(B=\sqrt{\frac{m}{\ln \ln n}}\)，总复杂度 \(O(\sqrt{\frac{m}{\ln \ln n}}\times n\ln \ln n)=O(n\sqrt{m\ln \ln n})\)，可以通过这道题。

接下来考虑如何实现修改。

对于每个 \(i\) 的每个不同质因数 \(p\)，维护 \(d_{p,i}\) 表示满足 \(\gcd(i,a_i\times p^{x+1})=\gcd(i,a_i\times p^x)\) 的最小的 \(x\)，再对于每个质数 \(p\) 维护一个 set 表示 \(d_p\) 的非零位置集合（这种方法好像叫做势能 set）。

修改时枚举 \(c\) 的质因子，利用 set 对于每个质因子枚举所有要修改的位置，进行修改并重构块。注意这里修改只改 \(f\) 并重构该块的 \(g,sum\)，不要修改 \(a\)。

一个更简单的维护方法是记 \(rd_i=\frac{i}{\gcd(i,a_i)}\)，每次修改 \(c\) 的一个质因子 \(p\) 时，在 \(rd_i\) 中移除尽可能多的 \(p\)，并贡献给 \(\gcd(i,a_i)\)，如果修改后 \(rd_i\) 中没有 \(p\) 因子，则将 \(i\) 移出 \(p\) 的 set。

最后散块的 \(a\) 暴力改，整块的 \(a\) 打 tag 即可。

查询时如果在散块操作要 pushdown。

提交记录

2025.7.20

P6157 有趣的游戏 紫

题意

维护一颗树，点有点权，支持：

• 单点修改
• 给定 \(u,v\)，求 \(\max\limits_{x,y\in \text{path(u,v)}} \{w_x\bmod w_y\}\)，设取到最大值的两点为 \(x,y\)，还需要求出 \(\max\limits_{1\leq a,b\leq n\land|\{a,b\}\cup\{x,y\}|=4} w_a\bmod w_b\)。

题解

发现取最大值和严格次大值时最优，链上取模最大值可以树剖维护。然后全局维护一个 multiset，负责查询去掉某两个数后的最大值和次大值即可。

提交记录

P4947 PION后缀自动机 紫

题意

给定一颗 \(n\) 个节点的树，每个节点中包含一些文件。

实现三个功能，这三个功能会被调用共 \(m\) 次：

1. 计算树上 \(u,v\) 两点的距离。
2. 计算 \(u,v\) 路径中文件名为 A 的文件数量。
3. 删除 \(u,v\) 路径中所有文件名为 A 的文件，并统计被删除文件的数量。

\(n,m<=10^5,文件总数\leq 5\times 10^5\)。

题解

对每个不同文件名分开做，然后树剖实现链覆盖 \(0\)，链求和即可。

提交记录

P5556 圣剑护符 紫

题意

维护一颗 \(n\) 个节点的树，点有点权，需要支持 \(q\) 次操作。

每个操作形式如下：

1. Update x y z：将 \(x\) 到 \(y\) 的路径上的点的点权全部异或上 \(z\)。

2. Query x y：设 \(x\) 到 \(y\) 的路径上的点的点权所组成的集合为 \(S\)，判断 \(S\) 是否存在两个不同子集异或和相同。

题解

注意到当 \(\operatorname{dist}(x,y)>30\) 时，\(S\) 一定存在两个不同子集异或和相同（由线性基的插入过程可说明）。

当 \(\operatorname{dist}(x,y)\leq 30\) 时，暴力将路径上的所有点的点权插入到线性基里面判断。

用树剖维护路径异或，单点查询。

提交记录

P5138 fibonacci 黑

题意

维护一颗 \(n\) 个节点的树，支持以下操作共 \(m\) 次：

• U x k：对于 \(x\) 及其子树内的节点，若其到 \(x\) 的距离为 \(D\)，则该点点权加 \(Fib_{D+k}\)。\(Fib\) 指斐波那契数列。
• Q x y：询问路径 \(x,y\) 上所有节点的点权之和，答案对 \(10^9+7\) 取模。

\(n,m\leq 10^5\)。

题解

先写出 Fib 矩阵 \(M=\begin{pmatrix} 1 & 1 \\ 1 & 0 \end{pmatrix}\)。

每个点维护两个矩阵 \(A,B\)，其中 \(A\) 固定，\(B\) 会因为修改操作改变。

记一个节点的深度为 \(dep\)，根的深度为 \(1\)，则令这个点的 \(A=M^{dep}\)。

对于子树 \(u\) 的加操作，转化为子树 \(u\) 的每个点的 \(B\) 加上 \(M^{k-dep_u+1}\)。

不难发现，一个点真正的 Fib 矩阵就是 \(A\times B\)，Fib 矩阵右下角即为这个点的点权。

使用重链剖分和 DFS 序，将树上问题转为序列问题。

序列问题是：每个下标有两个矩阵 \(A,B\)，需要支持 \(B\) 区间加，查询 \(A\times B\) 的和。

用线段树维护，线段树每个节点维护 \(Sa=\sum A\) 和 \(Sab=\sum A\times B\)，再维护一个懒标记 \(K\)。

对线段树上一个节点进行加 \(B\)，有 \(Sab\leftarrow Sab+Sa\times B\)，\(K\leftarrow K+B\)。

下传标记时，设线段树上当前节点的父节点为 \(fa\)，有 \(K\leftarrow K+K_{fa}\)，\(Sab\leftarrow Sab+Sa\times K_{fa}\)。

时间复杂度 \(O(n\log^2 n)\)，八倍常数。

提交记录

2025.7.21

AtCoder-ddcc2020_final_C - Smaller-Suffix-Free Sequences *????

复习 SA。

提交记录

P9664 [ICPC 2021 Macao R] LCS Spanning Tree 紫

题意

给定一个有 \(n\) 个顶点的完全无向图和 \(n\) 个字符串 \(s_1, s_2, \cdots, s_n\)，连接顶点 \(i\) 和 \(j\) 的边的权重等于字符串 \(s_i\) 和 \(s_j\) 的最长公共子串（LCS）的长度。计算此图的最大生成树。

题解

两个串求最长公共子串，可以拼在一起建立 SA，然后只考虑相邻两项的 LCP（即 height）。

推广到多个串，建出 SA 后只连接后缀排序中相邻两个字符对应字符串的边，也是对的。

因为如果一条边 \((a,c)\) 在后缀排序中跨过了另一个字符串 \(b\)，那么把边改成 \((a,b)(b,c)\) 更优。

提交记录

咕咕咕。

2025.7.22

CF1923F Shrink-Reverse *2800

题意

给你一个长度为 \(n\) 的 01 串 \(s\)，你可以进行 \(k\) 次操作。每次你可以从下面两种操作中选一种执行：

• 1. 选择两个位置 \(i \neq j\)，交换 \(s_i, s_j\)；
• 2. 将串的前导 \(0\) 清除之后翻转整个串 \(s\)。

你需要最小化至多 \(k\) 次操作后串在十进制意义下的值，对 \(10^9 + 7\) 取模并输出它。

\(2 \leq n \leq 5 \times 10^5\)，\(1 \leq k \leq n\)。

题解

发现翻转操作不会超过两次。

其次翻转肯定可以被放到最后，因为交换和翻转是独立的。

进一步我们发现反转操作不会超过一次，因为翻转两次是为了去掉后导零，然而翻转一次后已经去掉了前/后导零，因此可以把交换操作全部对称一下，然后只翻转一次。

讨论是否进行翻转：

• 不进行翻转：
  • 双指针维护第一个 \(1\) 和最后一个 \(0\) 进行交换即可。
• 进行翻转：
  • 我们需要先最小化长度，对于每个 \(i\)，找到最小的 \(R_i\) 满足 \([i,R_i]\) 有不少于 \(cnt1-k+1\) 个 \(1\) 和 \(k-1\) 个 \(0\)，这样才能把外面的 \(1\) 换到里面。
  • 其次因为要翻转，因此肯定是让 \(1\) 集中在前面，具体的，在 \([i,R_i]\) 中找到一个 \(r_i\) 满足 \([i,r_i]\) 中有 \(k-1\) 个 \(0\)，那么最后的形态肯定是 \([i,r_i]\) 全为 \(1\)，\([r_i+1,R_i]\) 保持不动。
  • 特殊的，如果 \(r_i=R_i\)，那么最后的序列全为 \(1\)。
  • 我们先选出 \([i,R_i]\) 尽可能短的一些 \(i\)，然后比较这些 \(i\) 的 \([r_i+1,R_i]\) 翻转后的字典序，注意这里比较字典序时，如果 \(A\) 是 \(B\) 的前缀，那么我们认为 \(B\) 的字典序比 \(A\) 小，因为 \([i,r_i]\) 全为 \(1\)，本质上是在 \(A,B\) 末尾都补了若干个 \(1\)。
  • 使用 SA 实现两个字符串字典序的比较函数，然后用比较函数进行排序。

提交记录

CF547E Mike and Friends *2800

题意

给定 \(n\) 个字符串 \(s_1,s_2,\dots ,s_n\)。

定义 \(\operatorname{call}(x,y)\) 表示 \(s_y\) 在 \(s_x\) 中出现的次数。

处理 \(q\) 次询问，每次给定 \(l,r,k\)，求 \(\sum\limits_{i=l}^{r} \operatorname{call}(i,k)\)。

\(n\leq 2\times 10^5,q\leq 5\times 10^5\)。

题解

建立 SA，对于 \(s_k\) 在 SA 中的第一个字符，二分出一个极长的 \(height\) 区间，满足这个区间的 \(height\) 都大于 \(\operatorname{len}(s_k)\)，记这个区间为 \([a,b]\)，那么答案就是 \(id\in [l,r]\) 且 \(rk\in [a,b]\) 的字符个数，二维数点即可。

提交记录

2025.7.23

P4094 [HEOI2016/TJOI2016] 字符串 黑

题意

给定一个长度为 \(n\) 的字符串，\(m\) 次询问，问子串 \(s[a..b]\) 的所有子串和 \(s[c..d]\) 的最长公共前缀的长度的最大值。

\(1\le n,m\le 100,000\)。

题解

与上一题类似。建立 SA，二分答案 \(x\)，对于 \(s_c\) 在 SA 中的第一个字符，二分出一个极长的 \(height\) 区间，满足这个区间的 \(height\) 都大于 \(x\)，记这个区间为 \([rkl,rkr]\)，那么如果存在一个字符 \(id\in [a,b]\) 且 \(rk\in [rkl,rkr]\)，则答案 \(\geq x\)，在线二维数点，使用主席树维护。

提交记录

P5161 WD与数列 黑

题意

定义两个序列 \(A,B\) 是匹配的，当且仅当 \(|A|=|B|\) 且对于 \(1\le i,j\le |A|,A_i-B_i=A_j-B_j\)。即长度相同且一个数列同时加上一个数可以和另一个数列完全一样。

给定一个长度为 \(n\) 的数列，求数列中有多少对不相交的子串使得他们是匹配的。

题解

匹配的条件是长度相同且差分数组相同，统计所有长度为 \(1\) 的数列对答案的贡献，然后将原序列求差分，问题转化为求一个字符串中有多少对不相交且相等的子串。

先不考虑不相交的限制，求有多少对相等的子串，相当于求 \(\sum\limits_{i=1}^{n}\sum\limits_{j=i+1}^{n} \operatorname{lcp}(s[i\cdots n],s[j\cdots n])\)，这个问题可以建出 SA 然后求 height 的区间 \(\min\) 的和来解决。

然后考虑把相交的串减掉，考虑相交的匹配串同时删去最后一个字符也是匹配的，且删除的临界是把两个串删成相邻的匹配串（即平方字符串）。记这个临界的字符串长度为相交匹配串的临界长度。

考虑【优秀的拆分】的套路，枚举临界长度 \(p\)，之后取出点集 \(\{1,p+1,2p+1,\dots\}\)，一个临界长度的串一定经过恰好一个点，因此枚举平方字符串经过的两个相邻点，之后求这两个位置的 \(\operatorname{lcs}\) 和 \(\operatorname{lcp}\)，分别记为 \(L_a\) 和 \(L_b\)，如果 \(L_a+L_b\geq p\)，则说明这对相邻点将产生一些相交的匹配串。

具体的，令 \(k=i+p-\min(La,p)+1,w=\min(La,p)+\min(Lb,p)-p\)，则多余的贡献是首项为 \(i+Lb-k+1\)，末项为 \(i+Lb-k+1-w+1\)，公差为 \(1\) 的等差数列的和。将这个贡献减去。取 \(\min\) 的原因是不能与跨过其他相邻点的平方字符串算重。

注意差分数组的相邻在原数组上算作相交。

完结散花。

提交记录

SP1812 LCS2 - Longest Common Substring II 紫

题意

给定一些字符串，求出它们的最长公共子串。

题解

对第一个串建 SAM，然后把后面的串依次在 SAM 上做匹配，记录到达每个点的最大长度 \(p\)，然后每个点对 \(n\) 个 \(p\) 取 \(\min\)，最后取值最大的点即可。

注意，因为这是 SAM，所以到达一个点相当于匹配上了这个点 fail 树的到根链，因此父节点要对子节点取 \(\max\)，当然每个节点还需要保证值不超过这个点的 \(\text{len}\)。

提交记录

2025.7.24

P4482 [BJWC2018] Border 的四种求法 黑

题意

给定一个长为 \(n\) 字符串 \(S\)，\(q\) 次询问，每次询问给出 \(l,r\)，求区间 \([l,r]\) 的 border。

\(n,q\leq 2\times 10^5\)。

题解

把 border 刻画为判定条件。

\([l,x]\) 是 \([l,r]\) 的 border，当且仅当 \(\operatorname{lcs}(s[1\cdots x],s[1,\cdots r])\geq x-l+1\)。

我们知道，两个前缀的 \(\operatorname{lcs}\)，是这两个前缀在 SAM 的 fail 树上的 \(\operatorname{lca}\) 的 \(\text{len}\)。

也就是说，求最大的 \(x\)，使得 \(len_{\operatorname{lca}(pos_x,pos_r)}\geq x-l+1\)。

点分治，把询问挂到 \(pos_r\) 上，在分治中心为 \(\operatorname{lca}(pos_x,pos_r)\) 时统计答案。

点分治时，确定分治中心为 \(w\)，遍历 \(w\) 向下的的每个子树，遍历到一个子树时，先考虑查询答案，设当前点为 \(t\)，则对于一个 \(pos_r=t\) 的询问 \((l,r)\)，在 \([l,r)\) 中找到一个 \(x\)，满足 \(pos_x\) 在之前的子树遍历到过，且 \(len_w\geq x-l+1\)，即 \(x\leq len_{w}+l-1\)。也就是说，我们可以找到编号在 \([l,len_{w}+l-1]\) 之间最大的 \(x\)，用 \(x-l+1\) 更新答案。

考虑如何维护，点分治遍历到一个子树时，更新完答案后，对于每个节点 \(u\)，将 \(pos_x=u\) 的 \(x\) 全部放到平衡树中，查询时在平衡树上找 \(len_{w}+l\) 的前驱即可。

但是我们还没有统计根向的路径。

对于根向路经 \((pos_x,pos_r)\)，当 \(r\) 在上 \(x\) 在下时，树上维护平衡树的启发式合并，使得树上遍历到点 \(p\) 时，所有 \(p\) 子树内的点都在平衡树里，然后对于 \(pos_r=p\) 的询问，查询 \(len_p+l\) 的前驱。

当 \(x\) 在上 \(r\) 在下时，根据 \(len_{pos_x}\geq x-l+1\)，有 \(x-len_{pos_x}\leq l-1\)，DFS 并使用线段树维护到根链的点集，线段树里下标为 \(x\) 的地方放入 \(x-len_{pos_x}\)，然后二分一个最大的 \(x\) 满足这个位置的值 \(\leq l-1\) 即可。

然后点分治没调出来，平衡树合并还被卡空间了，WA+MLE。

（todo）验证上述点分治的正确性？

---

我们发现上述方法违背了点分治的“本职工作”，我们钦定了分治中心为 \(\text{lca}\)，但点分治只保证在钦定路径经过分治中心时能够不漏的统计所有路径。

其实不用那么麻烦，我们给每条边赋一个边权，为 \(len_u-len_{fa_u}\)，然后可以用如下方式表示 \(\text{len}\)，\(len_{\operatorname{lca}(pos_x,pos_r)}\times 2=len_{pos_x}+len_{pos_r}-\operatorname{dist}(pos_x,pos_r)\)。

重新整理式子，\(len_{pos_x}+len_{pos_r}-\operatorname{dist}(pos_x,pos_r)\geq 2(x-l+1)\)，点分治时，令点 \(u\) 分治中心的边权和为 \(dis_u\)，则上述式子可进一步化简为 \(dis_{pos_r}-len_{pos_r}-2l\leq len_{pos_x}-dis_{pos_x}-2x-2\)。

这是一个二维数点问题，令一个点的属性为 \((x,y)=(x,len_{pos_x}-dis_{pos_x}-2x-2)\)，则对于一个询问 \((l,r)\)，有 \(x\in[l,r)\)，\(y\geq dis_{pos_r}-len_{pos_r}-2l\)。

然后我们发现点分治时不用扣除子树内部的贡献，因为子树内部会把 \(\text{dist}\) 算的更大。

然后直接二维数点就行了。

这种方法启示我们：可以把与 \(\text{lca}\) 相关的信息转化为与两点路径长度有关的信息，而对于路径长度，\(\operatorname{dist}(u,v)=dis_u+dis_v-2\times dis_{k}\) 在 \(k=\operatorname{lca'}(u,v)\) 时成立，其中 \(\operatorname{lca'}\) 表示将我们计算 \(dis\) 的方向作为根向的 \(\text{lca}\)，也就是说我们可以在点分治等算法中任意钦定“根”，从根开始计算 \(dis\)，利用这个式子进行一些操作。

这种方法适用于点分治计算与有根树 \(\text{lca}\) 相关的问题。

两只 \(\log\)，完结散花。

提交记录

P10780 BZOJ3028 食物 紫

学习生成函数。

提交记录

P6078 [CEOI 2004] Sweets 紫

题意

John 得到了 \(n\) 罐糖果。第 \(i\) 个糖果罐里有 \(m_{i}\) 个相同的糖果。John 决定吃掉 \(a\sim b\) 个糖果。求吃糖果的方案数。

题解

写出第 \(i\) 罐糖果的生成函数 \(\sum\limits_{j=0}^{m_i} x_j=\frac{1-x^{m_j+1}}{1-x}\)。

全部乘起来，就是 \(\left( \prod\limits_{i=1}^{n} 1-x^{m_i+1} \right)\times \frac{1}{(1-x)^{n}}\)，答案是这个式子 \(x^{a\sim b}\) 项的系数和。

\(\prod\limits_{i=1}^{n} 1-x^{m_i+1}\) 可以暴力。

\(\frac{1}{(1-x)^{n}}\) 使用牛顿二项式定理，得到 \(\sum\limits_{i\geq 0} \binom{n-1+i}{i} x^i\)。

不好直接乘，考虑暴力求完 \(\prod\limits_{i=1}^{n} 1-x^{m_i+1}\) 后，枚举每一项 \(px^k\)，这一项对答案的贡献为 \(p\) 乘上 \(\frac{1}{(1-x)^{n}}\) 的 \(x^{a-k\sim b-k}\) 项系数和，即 \(\sum\limits_{i=a-k}^{b-k} \binom{n-1+i}{i}\)。

根据 \(\binom{n-1}{m-1}+\binom{n-1}{m}=\binom{n}{m}\)，有：

\[\sum_{i=l}^{r} \binom{x+i}{i} \\ =\binom{x+l}{l-1}+\left( \sum_{i=l}^{r} \binom{x+i}{i} \right)-\binom{x+l}{l-1} \\ =\binom{x+r+1}{r}-\binom{x+l}{l-1} \]

套用这个公式，有：

\[\sum\limits_{i=a-k}^{b-k} \binom{n-1+i}{i} \\ =\binom{n+b-k}{b-k}-\binom{n-1+a-k}{a-k-1} \\ =\binom{n+b-k}{n}-\binom{n-1+a-k}{n} \]

因此枚举 \(\prod\limits_{i=1}^{n} 1-x^{m_i+1}\) 的每一项 \(px^k\)，对答案贡献为 \(p\times \left( \binom{n+b-k}{n}-\binom{n-1+a-k}{n} \right)\)。

计算组合数时，由于 \(n\) 很小，所以直接用 \(\binom{n}{m}=\frac{n^{\underline{m}}}{m!}\) 暴力计算即可。

由于模数不质，所以不能直接取模，但因为 \(m!\) 很小，所以可以计算 \(n^{\underline{m}}\bmod (2004\times m!)\)，最后在除以 \(m!\) 即为 \(\binom{n}{m}\)。

注意以下搜索边界，由于 \(\frac{1}{(1-x)^{n}}\) 的每一项次数都非负，所以搜索时系数不能超过 \(b\)。

这样比较麻烦，其实在计算 \(\binom{n}{m}\) 时把 \(n<m\) 的判成 \(0\)，也有同样的效果，因为当 \(k>b\) 时对答案贡献为 \(0\)，当 \(k>a-1\) 时对答案贡献为 \(\binom{n+b-k}{n}\)，即 \(\sum\limits_{i=0}^{b-k} \binom{n-1+i}{i}\)。

提交记录

2025.7.25

P3978 [TJOI2015] 概率论 紫

题意

对于一棵随机生成的 \(n\) 个结点的有根二叉树（所有互相不同构的形态等概率出现），它的叶子节点数的期望是多少呢？

题解

令 \(g_{x}\) 表示大小为 \(x\) 的二叉树个数，\(f_{x}\) 表示大小为 \(x\) 的二叉树叶节点个数之和。

有：

\[g_{x}=\sum\limits_{i=0}^{n-1} g_{i}\times g_{n-i-1} f_{x}=2\times \sum\limits_{i=0}^{n-1} f_{i}\times g_{n-i+1} \]

注意特殊位置：\(f_0=0,f_1=1\)。

写出 \(g\) 的生成函数 \(G\)，\(f\) 的生成函数 \(F\)。

仿照卡特兰数列推导方式，对于 \(F\) 的式子，有 \(xF(x)\times 2G(x)+x=F(x)\)，加 \(x\) 是因为 \(f_1=1\)。

然后由于 \(G\) 是卡特兰数的生成函数，因此 \(G(x)=\frac{1-\sqrt{1-4x}}{2x}\)，所以 \(F(x)=\frac{x}{(1-4x)^{0.5}}\)。

将 \((xG)\) 求导，得到 \((xG)'=\frac{1}{(1-4x)^{0.5}}=\frac{F}{x}\)。

因此，对于 \(xG\) 中的一项 \(xg_nx^{n}\)，求导后将变为 \((xg_nx^n)'=(g_nx^{n+1})'=(n+1)g_nx^n\)，由于 \((xG)'=\frac{F}{x}\)，所以 \((n+1)g_nx^{n}=\frac{f_{n+1}x^{n+1}}{x}\)，\(f_{n+1}=(n+1)g_n\)，\(f_n=n\times g_{n-1}\)。

将卡特兰数通项公式 \(g_n=\frac{\binom{2n}{n}}{n+1}\) 带入，得 \(f_n=\frac{(2n-2)!}{(n-1)!(n-1)!}\)。

由于我们要求期望，因此最后要除以 \(g_n\)，最终答案为 \(\frac{n(n+1)}{2(2n-1)}\)。

提交记录

[ABC231G] Balls in Boxes 紫

题意

有 \(N\) 个编号为 \(1\) 到 \(N\) 的箱子。最初，第 \(i\) 个箱子中有 \(A_i\) 个球。

你需要重复进行 \(K\) 次如下操作：

• 从 \(N\) 个箱子中等概率地随机选择一个（每次操作的选择相互独立）。在选中的箱子中加入 \(1\) 个球。

\(K\) 次操作结束后，设第 \(i\) 个箱子中的球数为 \(B_i\)，则得分为所有箱子球数的乘积 \(\prod_{i=1}^{N} B_i\)。

请你计算得分的期望值，并对 \(998244353\) 取模。

题解

生成函数，推式子。

记一个数被操作了 \(p\) 次，则第 \(i\) 个盒子的生成函数是 \(F_i (x)=\sum_{p_i\geq 0} \frac{(a_i+p_i)}{p_i!}x^{p_i}\)，答案为 \(\frac{[x^k]\prod\limits_i F_i (x)\times k!}{n^k}\)。

其中 \(\frac{k!}{\prod p!}\) 是因为形成最终局面的操作方案有 \(\frac{k!}{\prod p!}\) 种。

\[F(x)=\sum_{i\geq 0} (a_i+i)\times \frac{x^i}{i!} \\ =a_i\left( \sum_{i\geq 0} \frac{x^i}{i!} \right)+\sum_{i\geq 0} i\frac{x^i}{i!} \\ =a_i e^x+xe^x \\ =(x+a_i)e^x \]

\[\prod F_i (x) \\ =e^{nx}\times \prod (x+a_i) \\ e^{nx}=\sum n^i\times \frac{x^i}{i!} \]

记 \(\prod (x+a_i)\) 的 \(x^i\) 项系数为 \(c_i\)，则答案为：

\[\frac{[x^k]\prod F_i (x)\times k!}{n^k} \\ =\sum\limits_{i=0}^{\min(n,k)} \frac{n^{k-i}}{(k-i)!}\times c_i\times \frac{k!}{n^k} \\ =\sum\limits_{i=0}^{\min(n,k)} \frac{\prod_{j=k-i+1}^{k}j}{n^i}\times c_i \]

时间复杂度 \(O(n^2)\)。

提交记录

2025.7.26

咕咕咕咕咕

2025.7.27

CF891E Lust *3000

题意

你有 \(n\) 个数 \(a_1, a_2, \dots, a_n\) 要进行 \(k\) 次操作，每次随机选择一个数 \(x \in [1, n]\)，把 \(a_x\) 减一，并将答案增加除 \(a_x\) 外所有数的乘积。

求最终答案的期望，答案对 \(10^9+7\) 取模。

题解

发现原序列乘积减去新序列乘积即为答案。

与 [ABC231G] Balls in Boxes 相同。

提交记录

P2012 拯救世界2 黑

学习指数生成函数。

提交记录

2025.7.28

P5521 [yLOI2019] 梅深不见冬 蓝

题意

给定一颗树，你要按照某个 DFS 序走遍这棵树，到达一个节点时，你可以在节点放置若干个果实。你也可以任意时刻任意地点回收某个节点的果实。（无需到达被回收节点）

你在 \(u\) 放置果实时，需要满足对于 \(u\) 的所有儿子 \(v\)，节点 \(v\) 都放置了 \(w_v\) 个果实。

对于每个节点 \(u\) 求出，想要在这个节点放置 \(w_u\) 个果实，至少需要携带多少个果实。

题解

考虑 DFS 序确定时，可以树形 DP，令 \(f_u\) 表示点 \(u\) 的答案，有：

\[f_u=\max(\max\{ans_v+\sum_{x\in son_u\land dfn_x<dfn_v} w_v\},w_u+\sum_{v\in son_u} w_v) \]

也就是说我们要给每个点子节点排序使这个值最小，邻项交换即可得出应该按 \(w-f\) 升序排序。

提交记录

CF1601D Difficult Mountain *2700

题意

\(n\) 个人相约去爬山。山的初始攀登难度为 \(d\)。每位登山者有两个属性：技巧 \(s\) 和整洁度 \(a\)。技巧为 \(s\) 的登山者能登上攀登难度为 \(p\) 的山当且仅当 \(p\leq s\)。在一位整洁度为 \(a\) 的登山者登上攀登难度为 \(p\) 的山后，山的攀登难度会变为 \(\max(p,a)\)。

请给这些登山者指定一个爬山的先后顺序，最大化登上山的人数。

\(n\leq 5\times 10^5\)。

题解

一个属性为 \((s,a)\) 的人登山成功后，如果 \(s<a\)，那么山的高度一定会变为 \(a\)，否则山的高度不确定。因此按照 \([s<a]\) 把登山的人分成两类。

对于 \(a\leq s\) 的人构成的集合，按 \(a\) 排序或者按 \(s\) 排序都行。

对于 \(s<a\) 的集合，显然按 \(a\) 排序最优，当 \(a\) 相等时顺序任意。

考虑合并两个集合。

假设 \(a_i\leq s_i,a_j>s_j\)，大力分讨。

1. \(a_i\leq s_i\leq s_j<a_j\) 显然选择 \(i\) 先。
2. \(a_i\leq s_j\leq s_i\leq a_j\) 显然选择 \(i\) 先。
3. \(a_i\leq s_j\leq a_j\leq s_i\) 谁先都一样。
4. \(s_j\leq a_i\leq s_i\leq a_j\) 谁先都只能有一人登山成功，因此我们要最小化山的高度，选 \(i\) 先。
5. \(s_j\leq a_i\leq a_j\leq s_i\) 显然选择 \(j\) 先。
6. \(s_j<a_j\leq a_i\leq s_i\) 显然选择 \(j\) 先。

注意到 \(\max(a,s)\) 取到最大值的那组肯定在后面。因此不同集合之间应该按 \(\max(a,s)\) 从小到大合并。

但是当 \(\max(a_i,s_i)=\max(a_j,s_j)\) 时，发现情况四可以有两个人登山成功了，此时要先选 \(j\)，对于其余五种情况，情况一根本不能取等，情况三、五、六的选择不改变。对于这种情况，\(s\) 小的肯定在前面，所以我们修正贪心策略，按 \(\max(a,s)\) 为第一关键字，\(s\) 为第二关键字，从小到大合并两个集合。

到这里题目已经做完了，但是我们有更简单的实现方式。其实按 \(\max(a,s)\) 为第一关键字，\(s\) 为第二关键字从小到大排序也适用于 \(s<a\)（此时第一关键字取等一定是 \(a_i=a_j\)）和 \(a\leq s\) 的两个集合内部，因此直接排序即可。

我们还要补充一个结论的证明：当前尽可能多个人登山一定不劣。发现除了情况五，我们都选择了 \(a\) 更小的先登山，这个结论是显然的。对于情况五，山的高度被提高了，如果后面存在一个人 \((a_k,s_k)\)，按照排序规则，要么 \(a_k\geq a_j\)，要么 \(s_k\geq a_j\)，前者可以不让 \(j\) 登山，换来 \(k\) 登山，但是山高增加了，不优。后者完全不影响。因此结论得证。

提交记录

2025.7.29

CF436E Cardboard Box *2600

题意

\(n\) 个关卡，对每个关卡，你可以花 \(a_i\) 代价得到一颗星，也可以花 \(b_i\) 代价得到两颗星，也可以不玩。问获得 \(w\) 颗星最少需要多少时间。

\(n\leq 3\times 10^5\)。

题解

把题目转换成每个关卡有两种操作：

1. 花费 \(a\) 获得一颗星
2. 再花费 \(b-a\) 获得一颗星

考虑反悔贪心，增加一颗星的方式有：

1. 直接选择：选择没玩过的关卡，改选 \(a\)。
2. 直接选择：选择一个选 \(a\) 的关卡，增加 \(b-a\)。
3. 反悔：选择一个选 \(a\) 的关卡，改为不选。然后在一个没玩过的关卡选择 \(b\)。
4. 反悔：选择一个选 \(b\) 的关卡，改为选 \(a\)。然后在一个没玩过的关卡选择 \(b\)。

对于操作一，维护一个小根堆表示没玩过的关卡中 \(a\) 的集合。
对于操作二，维护一个小根堆表示选 \(a\) 的关卡中 \(b-a\) 的集合。
对于操作三，维护一个大根堆表示选 \(a\) 的关卡中 \(a\) 的集合，再维护一个小根堆表示没玩过的关卡中 \(b\) 的集合。
对于操作四，维护一个大根堆表示选 \(b\) 的关卡中 \(b-a\) 的集合，再维护一个小根堆表示没玩过的关卡中 \(b\) 的集合。

去重后总共要维护五个堆。

每个堆写成自动删除堆，即：元素写成二元组表示值和下标，操作时实时更新每个关卡的选择状态，对于一个堆，查询最值时先 pop 掉选择状态不符合要求的元素。

提交记录

P3620 [APIO/CTSC2007] 数据备份 蓝

题意

给定一个数组，两个数配对的代价是两数差的绝对值，选出 \(k\) 对不相交的匹配使得代价最小

题解

求出差分数组，即选出 \(k\) 个不相邻的位置使得代价最小。

这是经典的反悔贪心问题，解法是链表维护 01 交替的区间左右端点和改变代价，然后使用优先队列进行贪心。

提交记录

P3045 [USACO12FEB] Cow Coupons G 紫

题意

FJ 准备买一些新奶牛。市场上有 \(N\) 头奶牛，第 \(i\) 头奶牛价格为 \(P_i\)。FJ 有 \(K\) 张优惠券，使用优惠券购买第 \(i\) 头奶牛时价格会降为 \(C_i\)，当然每头奶牛只能使用一次优惠券。FJ 想知道花不超过 \(M\) 的钱最多可以买多少奶牛？

题解

反悔贪心。

新增加一头牛的方法有：

• 花费 \(P_i\) 购买。
• 花费一张券，并花费 \(C_i\) 购买。
• 将已经购买的一头牛的券撤回，并用这张券以 \(C_i\) 价格购买新的奶牛。

维护 \(P_i,C_i,P_i-C_i\) 的小根堆即可。

提交记录

2025.7.31

P4597 序列 sequence 紫

题意

给定一个序列，每次操作可以把某个数 +1 或 −1。要求把序列变成非降数列。

题解

设计 \(dp_{i,j}\) 表示前 \(i\) 个数，\(a_i=j\) 的最小操作数。

\(dp_i\) 是凸的，使用大根堆维护拐点，如果斜率变化量是 \(2\) 就认为拐了两次，分类讨论加入一个数时斜率的变化即可。

提交记录

agc034_c Tests *????

题意

给定非负整数序列 \(\{l_n\},\{r_n\},\{b_n\},X\)，求最小的 \(s\)，使得存在非负整数序列 \(\{a_n\},\{c_n\}\)，满足 \(a_i\le X\)，\(\sum_{i=1}^n a_i=s\)，\(c_i\in[l_i,r_i]\)，且

\[\sum_{i=1}^n c_i(a_i-b_i)\ge 0 \]

所有输入均 \(\le 10^5\)。

题解

容易发现 \(c_i\) 只有 \(l_i\) 和 \(r_i\) 两种取值，并且 \(a_i\) 只有一个地方取到 \(0\) 和 \(X\) 以外的值，这个结论可以通过调整法说明。

然后二分答案，算出 \(a_i=X\) 的个数 \(t=\lfloor \frac{mid}{X} \rfloor\)，枚举取到 \(0\) 和 \(X\) 以外的值的位置，在剩余的位置中贪心选变化量最大的 \(t\) 个即可。

这个过程可以前缀和优化，复杂度 \(O(n\log^2 n)\)。

提交记录