2025.6 做题记录

2025.6.1

小奇的博弈 紫难度

题意

\(1\times n\) 的棋盘上有 \(k\) 个白黑交替的棋子，两玩家博弈，每次玩家 \(1/2\) 可以将 \(1\sim d\) 个 白/黑 棋子移动若干格，不能跨过其他棋子或出界，不能操作者输，对必胜局面计数。

题解

设相邻白-黑的间距大小为 \(g_1,g_2,\dots g_{\frac{k}{2}}\)，则问题可以转化为有 \(\frac{k}{2}\) 堆石子，每次取走 \(1\sim d\) 堆石子的任意个石子，不能操作者输。

这是 NIM 游戏的拓展，必败条件是石子个数二进制不进位加法和的每一位模 \((d+1)\) 为 0。

如果确定了 \(\sum_i g_i\)，则可以通过组合数算出方案数，因此考虑对 \(\sum_i g_i\) 进行 DP。

\(dp_{i,sumd}\) 表示考虑二进制前 \(i\) 为，\(\sum_i g_i\) 和为 \(sumd\) 的方案数。

则有转移方程 \(dp_{i,sumd}\leftarrow \sum\limits_{0\leq j\times (d+1)\leq \frac{k}{2}\land sumd-2^{i}\times j\times (d+1)\geq 0} dp_{i-1,sumd-2^{i}\times j\times (d+1)}\times \binom{\frac{k}{2}}{j\times (d+1)}\)。

最后枚举 \(\sum_i g_i\) 计算必败情况数 \(res\)，则答案为 \(\binom{n}{k}-res\)。

提交记录

CF1062F Upgrading Cities *2900

题意

给定一张有向无环图，若节点 \(x\) 满足至多存在一个节点 \(y\)，使得 \(x\) 和 \(y\) 互相不可达，则 \(x\) 节点是关键点，求关键点的个数。

题解

看到 DAG 可达性问题，考虑拓扑排序。

显然，拓扑排序的任意时刻，在队列中的点两两不可达。

记 \(u\) 能到达的点个数和能到达 \(u\) 的点个数之和为 \(cnt_u\)（不含 \(u\)），当 \(cnt_u\geq n-2\) 时 \(u\) 合法。

分析节点 \(u\) 出队列后时的队列大小 \(|Q|\)。记 \(u\) 是第 \(i\) 个出队的节点。

  • \(|Q|=0\)
    • 后面没有入队的点都可以从 \(u\) 到达，\(cnt_u\leftarrow cnt_u+n-i\)。
  • \(|Q|=1\)
    • 记 \(v\) 为队列中的元素。
    • 如果存在边 \((v,w)\) 且此时 \(w\) 入度为 \(1\)，则 \(v,w\) 都与 \(u\) 不可达，\(u\) 不合法，\(cnt_u\leftarrow -\infin\)。
    • 否则 \(u\) 可以到达的点数为后面没有入队的点减 \(1\)，\(cnt_u\leftarrow cnt_u+n-i-1\)。
  • \(|Q|\geq 2\)
    • 显然 \(u\) 不合法，\(cnt_u\leftarrow -\infin\)。

正着做一遍，之后把边反转在做一遍，统计 \(cnt_u\geq n-2\) 的个数即可。

提交记录

P4630 [APIO2018] 铁人两项 紫

题意

给定一张简单无向图，问有多少三元组 \((s,c,f)\)，满足 \(s,c,f\) 互不相同，且存在一条 \(s\rightarrow c\rightarrow f\) 的简单路径。

题解

学习圆方树做的第一题。

点双的性质之一是任意两点的简单路径并等于整个点双。

建出圆方树后，确定起点和终点，则中转点的方案数就是路径上所有方点所属点双的并集大小减 \(2\)（减去起点和终点）。

将方点点权设为所属点双大小，圆点点权设为 \(-1\)，则两点在圆方树上的点权和恰好是所有方点所属点双的并集大小减 \(2\)。

于是问题转化为统计圆方树上所有有序点对路径中点权之和，可以用简单的树上 DP 实现。

提交记录

P9829 [ICPC 2020 Shanghai R] Traveling Merchant 紫

题意

给定一张简单无向图，点权为 \(0\) 或 \(1\)，从 \(1\) 号点开始行走，每次只能走两端点权不同的边，每次离开一个点的时候该点的点权自动取反，判断是否存在一种经过无穷个点的行走方案。

题解

分析性质，存在无穷路径，当且仅当：存在一个奇环，恰有一条同色边，且同色边的一个端点可以作为起点。

即同色边的一个端点可以从 \(1\) 不经过环上节点达到。

只加入异色边，则存在无穷盈利的路径可以等价为存在一条同色边 \((u,v)\)，满足：

  • 存在一条从 \(1\) 开始，顺次经过 \(1\rightarrow u\rightarrow v\) 或 \(1\rightarrow v\rightarrow u\) 的简单路径。
    • 解释一下：
    • 其中 \(u\rightarrow v\)（或 \(v\rightarrow u\)）是奇环上路径，\(1\rightarrow u\) （或 \(1\rightarrow v\)）表示不经过环上路径的前提下从 \(1\) 到 \(u\)（或 \(v\)）。
    • 由于要求简单路径，所以上述性质得到保证。

三点连通性问题，考虑圆方树。

利用圆方树的性质，存在 \(1\rightarrow u\rightarrow v\) 的简单路径，等价于：

  • 圆方树以 \(1\) 为根，存在两个方点 \(p,q\)，满足圆点 \(u\) 属于方点 \(p\)，圆点 \(v\) 属于方点 \(q\)，且 \(p\) 为 \(q\) 的祖先。

问题在于一个圆点可能属于多个方点。贪心的，我们取 \(u\) 在圆方树上的父亲节点 \(fa_u\) 作为 \(u\) 所属的方点。

容易证明，此时 \(v\) 属于哪个方点是无关紧要的，为了方便可以取 \(fa_v\) 作为 \(v\) 所属的方点。

所以枚举同色边 \((u,v)\)，判断 \(fa_u\) 和 \(fa_v\) 是否构成祖孙关系即可（注意特判 \(1\) 号点）。只要有一条同色边符合条件答案就是 yes，否则答案为 no。

提交记录

2025.6.2

agc071_c Orientable as Desired *2740

题意

给定一个简单连通无向图 \(G\)，判断是否存在满足以下所有条件的长度为 \(N\) 的非负整数序列 \(X = (X_1, X_2, \dots, X_N)\)：

  • 对于每个 \(v = 1, 2, \dots, N\)，\(X_v\) 不超过图 \(G\) 中顶点 \(v\) 的度数
  • 不存在一种对 \(G\) 的 \(M\) 条边进行定向的方法，使得得到的有向图中每个顶点 \(v\) 的入度或出度等于 \(X_v\)

题解

先摆结论。如果且仅如果同时满足以下两个条件，就不存在可行的 \(X\)：

  1. \(G\) 是二分图；
  2. 对图中每个顶点 \(v\)，把与 \(v\) 相邻的边按照它们所在的点双进行分类。设这些类别的大小分别为 \(c_1,c_2,\dots,c_k\)，那么必须能用这些 \(c_i\) 的某个子集之和，表示从 \(0\) 到 \(\deg(v)=c_1+c_2+\cdots+c_k\) 之间的每一个整数。

思考过程与证明如下：

令 \(X = (0, 0, \dots, 0)\)。发现一个点要么入度为 \(0\)，要么出度为 \(0\)，且相邻点的情况不能相同。因此如果 \(G\) 不是二分图，答案为 Yes。

下面只考虑 \(G\) 是二分图的情况。

令 \(X = (0, 0, \dots, X_u, \dots, 0)\)。如果 \(u\) 和 \(u\) 的两个相邻点 \(a,b\) 在同一点双内，即 \(a\) 不经过 \(u\) 能到达 \(b\)，由于 \(G\) 是二分图， \(a\) 和 \(b\) 与 \(u\) 的边方向一致。

因此将 \(u\) 的相邻边根据所在点双分类，设这些大小为 \(c_1,c_2,\dots,c_k\)。

那么相当于要选出 \(c_i\) 的某个子集作为 \(u\) 的入度或出度，选不出来即无解。

因此必要性得证，接下来证明充分性。

如果原图是一棵树，那么可以自上而下进行构造，显然能通过调整子节点构造出合法方案。

对于原图不是树的情况，建出圆方树，先按 \(X\) 全零构造，之后调整。自上而下调整，此时一个点的子节点表示一个点双。节点 \(u\) 向上指的边方向肯定是相同的，因此可以通过调整 \(u\) 子节点所对点双来组成任意的 \(X_u\)。

因此充分性得证。

提交记录

CF475E Strongly Connected City 2 *2700

题意

给一个无向图，你需要给所有边定向，使定向之后存在最多的点对 \((a,b)\) 使得从 \(a\) 能到 \(b\)。

题解

对于边双内部的点和边，肯定存在一种定向方式使得这些点互相可达。具体定向方式是选出一个环，环上边顺时针定向，环外点至少有两条边不重复到环上的路径（因为这是边双），令这两条路径方向相反即可。

将边双缩为一个点，原图变为一棵树，点有点权。问题转化为带权的树上问题。

猜测最优解树的形态如下：

树的形态

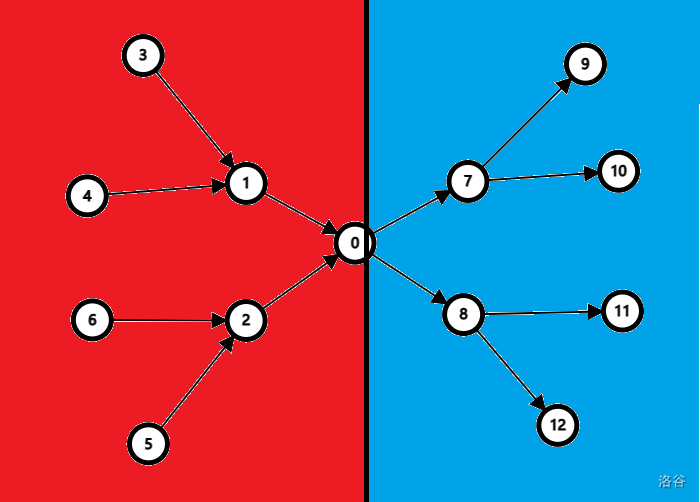
证明：

即证明上述树形态可以经过若干次不优调整变为任意形态。

只考虑蓝色区域调整，红色区域同理。考虑一条边 \((u,v)\) 的翻转，翻转前答案为 \(ans_u+ans_v+sz_u\times sz_v\)，翻转后答案为 \(ans_u+ans_v+sz_u\)，此处 \(sz_u\) 表示这条边 \(u\) 方向连通快的信息，而非子树信息。其余变量名同理。显然调整不优。

(todo) : 证明多次调整仍然不优。

简单分析即可得出两边大小尽可能平均，因此：非重心直接选重儿子放一边，轻儿子放一边；重心对子树大小背包即可。

朴素背包可以通过，无需 bitset 优化。

提交记录

CF1338E JYPnation *3500

题意

给定一张 \(n\) 个点的竞赛图，特别地，满足图中不存在如下这样的四个点 \(a, b, c, d\)：

  • 其中 \(a, b, c\) 三个点形成三元环，即 \(a \to b \to c \to a\)，且它们都向 \(d\) 连边，即 \((a, b, c) \to d\)。

计算 $ \sum_{1 \le i < j \le n} \text{dis}(i, j) $

如果 \(x\) 无法到达 \(y\) 则规定 \(\text{dis}(x, y) = 614 \times n\)。

\(n\leq 8000\)。

题解

首先如果两个点不在同一 SCC 中，则贡献为 \(614n+1\)，下面只考虑两点在同一 SCC 的情况。

首先 \(dis(u,v)\leq 3\)，因为如果 \(dis(u,v)=4\) 则存在不合法的导出子图（如图）。

考虑对 \(dis(u,v)=1\) 和 \(dis(u,v)=2\) 的点对计数，前者就是 SCC 内的边数，重点考虑后者。

\(dis(u,v)=2\)，当且仅当：

  • 不存在 \(u\rightarrow v\) 的边。
  • 存在 \(u\rightarrow a\) 和 \(a\rightarrow v\) 的边。

直接做是 \(O(n^3)\) 的，瓶颈在于需要枚举 \(u\) 的相邻点 \(a\)。

继续分析性质，如果存在边 \(v\rightarrow u\)，\(u\rightarrow a\)，\(a\rightarrow v\)，\(u\rightarrow b\)，\(a\rightarrow b\)，则必定存在边 \(b\rightarrow v\)。

这告诉我们如果 \(u\) 的邻点中存在 \(a,b\) 和边 \(a\rightarrow b\)，则没必要枚举 \(a\)，此时称 \(b\) 支配了 \(a\)。进一步，由于这是竞赛图，因此 \(u\) 的邻点中存在一个导出子图，满足这个子图是 SCC，且不被任何其他邻点支配。找到其中一个点判断是否能到 \(v\) 即可。

时间复杂度 \(O(n^2)\)，由于本题存在不缩点、常数更优秀的算法，因此这个算法需要卡常。

卡常技巧：注意数组访问顺序，循环时将数组缓存到局部指针。

提交记录

2025.6.3

CF1864H Asterism Stream *3200

题意

给定变量 \(x\)，初始为 \(1\)，每次等概率随机进行以下两种操作之一：

  1. \(x\leftarrow x+1\)

  2. \(x\leftarrow x\times 2\)

求期望多少次操作之后 \(x\geq n\)，对 \(998244353\) 取模。

题解

\(E(x\geq n)=\sum\limits_{i=1}^{n-1} P(x=i)\)。

问题转化为求解若干次操作后，\(x<n\) 的概率之和。

以下令 \(n:=n-1\)。

考虑枚举操作二的次数，然后在操作二之间穿插操作一。

设操作二的个数为 \(L\)，在倒数第 \(i\) 个操作二后进行的操作一会被放大 \(2^{i-1}\) 倍，因此本质上是对满足如下条件的序列 \((c_0,c_1,\dots,c_{L+1})\) 计数，其中序列 \((c_0,c_1,\dots,c_{L+1})\) 的权重为 \(2^{-\sum\limits_{i=1}^{L+1} c_i}\)。（注意 \(c_0\) 仅仅是把小于变为等于，并没有实际含义，也不计入权重中概率运算）

  • \(c_0+c_1+c_2\times 2^1+c_3\times 2^{2}+\cdots+c_{L+1}\times 2^{L}+2^L=n\)。

加上 \(2^L\) 是因为 \(x\) 初始为 \(1\)。

考虑将 \(c\) 拆为二进制，记 \(a[b]\) 表示 \(a\) 在二进制下第 \(b\) 为的值（\(0\) 或 \(2^b\)）。

原条件为：

\[(\sum_i c_0[i])+(\sum_i c_1[i])+(\sum_i c_2[i])\times 2^1+(\sum_i c_3[i])\times 2^{2}+\cdots+(\sum_i c_{L+1}[i])\times 2^{L}=n-2^L \]

考虑答案也拆为二进制，进行数位 DP。

其中答案的 \(2^i\) 系数为：

\[c_0[i]+c_1[i]+c_2[i-1]+c_3[i-2]+\cdots +c_{\min\{i+1,L+1\}}[i-\min\{i+1,L+1\}+1] \]

令 \(f_{i,j}\) 表示 \(2^{-(c_0[i]+c_1[i]+c_2[i-1]+c_3[i-2]+\cdots +c_{\min\{i+1,L+1\}}[i-\min\{i+1,L+1\}+1])}\) 之和，可以简单背包算。

之后就是基本的数位 DP，\(dp_{i,j}\) 表示正在决策自低向高的第 \(i\) 位，上一位进位为 \(j\) 的权重和，转移为：

\[dp_{i+1,\lfloor \frac{(j+k)}{2}\rfloor } \leftarrow dp_{i,j}\times f_{i,k} \ \ \ ((j+k)\equiv \lfloor \frac{n}{2^i}\rfloor\pmod 2) \]

提交记录

CFgym102411D Double Palindrome *????

题意

定义一个字符串是好的，当且仅当它要么本身是一个回文串，要么能被划分成两个回文串。

给定 \(n,k\)，求长度不超过 \(n\)，字符集大小为 \(k\) 的好的字符串个数，对 \(10^{9}+7\) 取模。

题解

定义一个串是本原的当且仅当其有唯一方式拆分成两个回文串。

如果我们能证明一个符合条件的串一定能够被一个本原串循环拼出来，且方案唯一，则我们可以通过如下方式计数：

  • 令 \(f_i\) 表示长度为 \(i\) 的符合条件字符串之和，但是其中一个字符串会被算重【划分方案】次。

  • \[f_{i}=\sum\limits_{i=0}^{n-1} k^{\lceil \frac{i}{2} \rceil+\lceil \frac{n-i}{2} \rceil}=\left\{\begin{matrix} n\times k^{\frac{n}{2}+1} (n\equiv 1\pmod 2) \\ \frac{n}{2}\times k^{\frac{n}{2}}+\frac{n}{2}\times k^{\frac{n}{2}+1} (n\equiv 0\pmod 2) \end{matrix}\right.\]

  • 令 \(g_i\) 表示长度为 \(i\) 的本原串个数，但是其中一个字符串会被算重【划分方案】次。显然本原串划分方案为 \(1\)，因此 \(g_i\) 实际不会算重。
  • \(g_i=f_i-\sum\limits_{d|n\land d\neq n} g_d\times \frac{n}{d}\)，乘上 \(\frac{n}{d}\) 表示乘上不是本原串中算重的部分。

接下来证明结论。

  • 若一个串 s 有至少两种拆分方式，则存在一个本原串循环节。

    • （todo）

  • 所有本原串复制若干遍得到的串不同。

    • （todo）

提交记录

2025.6.4

P9563 Be Careful 2 黑

题意

\(n\times m\) 的平面上有 \(k\) 个点，求平面上不包含这些点的正方形面积之和。

题解

考虑容斥，枚举被包含的点集 \(S\)，设完全包含 \(S\) 的正方形面积和为 \(f_S\)，则答案为 \(\sum\limits_{S} f_S\times (-1)^{|S|}\)。

完全包含 \(S\)，即完全包含 \((Xmin(S),Ymin(S)),(Xmax(S),Ymax(S))\) 这个矩形。

注意到如果这个矩形内部有点，那么这个点选或不选，对答案造成的贡献为相反数，可以抵消。

因此真正有用的矩形满足只有边界上有禁止点。

为了避免算重，可以离散化时维护一个严格偏序关系，这样离散化后任意两点 \(x,y\) 都不同，并且一个 \(y\) 对应唯一的 \(x\)。

具体的，离散化二分查找时这样写：

for(int i=1;i<=k;i++){
	a[i].x=lower_bound(bx+1,bx+1+k,a[i].x)-bx;
	bx[a[i].x]--;//变化在这里
	a[i].y=lower_bound(by+1,by+1+k,a[i].y)-by;
	by[a[i].y]--;//变化在这里
}

之后枚举矩形的 \(Ymin\) 和 \(Ymax\)（分别记为 \(y1,y2\)），根据上下 \(y\) 值找到唯一对应的两个点 \((x1,y1),(x2,y2)\)，则矩形左右边界一定是 \(x1,x2\) 或者 \(x1,x2\) 在 \(y\in (y1,y2)\) 的点中的某个前驱或后继。需要保证矩形内部没有点。

为了避免求前驱后继的 \(log\) 因子，枚举矩形可以这么写（\(rk_i\) 表示离散化后 \(y=i\) 的点的 \(x\) 值）：

for(int yl=1;yl<=k;yl++){
	sub(ans,calc(rk[yl],rk[yl],yl,yl));
	int mn=0,mx=k+1;
	for(int yr=yl+1;yr<=k;yr++){
		int xl=rk[yl],xr=rk[yr];
		if(xr<mn||xr>mx) continue;
		if(xr>xl){
			add(ans,calc(xl,xr,yl,yr));
			sub(ans,calc(xl,mx,yl,yr));
			sub(ans,calc(mn,xr,yl,yr));
			add(ans,calc(mn,mx,yl,yr));
			mx=xr;
		}else{
			add(ans,calc(xr,xl,yl,yr));
			sub(ans,calc(xr,mx,yl,yr));
			sub(ans,calc(mn,xl,yl,yr));
			add(ans,calc(mn,mx,yl,yr));
			mn=xr;
		}
	}
}

最后会产生 \(O(k^2)\) 个矩形，需要我们 \(O(1)\) 计算包含矩形的正方形面积之和。

正方形有三个属性——边长 \(d\)，左下角 \(x\)，左下角 \(y\)。

若一个正方形 \((d,x,y)\) 包含矩形 \((xl\sim xr,yl\sim yr)\) 且不出界，则需要满足：

  • \(\max\{xr-xl,yr-yl\}\leq d\leq \min\{n,m\}\)

  • \(0\leq x\leq xl,xr\leq x+d\leq n-d\)

  • \(0\leq y\leq yl,yr\leq y+d\leq m-d\)

满足条件的正方形 \((d,x,y)\) 贡献为 \(n^2\)。

因此答案为：

\[\sum\limits_{d=\min\{n,m\}}^{\max\{xr-xl,yr-yl\}} d^2\times ((\min\{xl,n-d\}-\max\{0,xr-d\}+1)\times (\min\{yl,m-d\}-\max\{0,yr-d\}+1) \]

这是一个不超过 \(5\) 段的四次分段函数，每一段形如 \(\sum\limits_{i=l}^r ai^4+bi^3+ci^2+di^1+e\)。

我们有公式：

\[\sum_{k=1}^{n} k = \frac{n(n+1)}{2}\\\sum_{k=1}^{n} k^{2} = \frac{n(n+1)(2n+1)}{6}\\\sum_{k=1}^{n} k^{3} = \left( \frac{n(n+1)}{2} \right)^{2}\\\sum_{k=1}^{n} k^{4} = \frac{n(n+1)(2n+1)\bigl(3n^{2}+3n-1\bigr)}{30} \]

因此直接计算即可。

提交记录

[ARC138F] KD Tree 黑

题意

给定一个长为 \(n\) 的点列 \((i,p_i)\)，其中 \(\{p_i\}\) 是一个 \(1\) 到 \(n\) 的排列。

每次操作可以选择 \(x/y\) 和一个坐标，将点列分成左右/上下两边（保持两边的相对顺序不变），分别递归下去，直到只剩下一个点，把它加入答案序列末尾。

求最终能生成多少种不同的答案序列，对 \(10^9+7\) 取模。

\(n\leq 30\)。

题解

让我们假定每次划分操作都会与至少一个点重合，这些重合点会被分到左/上部分。

显然一个结果序列会对应多个操作序列，考虑选取代表元。

贪心地从结果序列反向构建操作序列，按照 \(x,y\) 操作交替的顺序从小到大构造。

如果有 \(k+1\) 个点，那么将点离散化后可能进行的操作为 \(x=2,y=2,x=3,y=3,\dots x=k,y=k\)。依次尝试直到遇到符合条件的操作进行操作即可。

同时我们定义一步操作的字典序为在 \(x=2,y=2,x=3,y=3,\dots x=k,y=k\) 这个序列里的排名。

使用 \(dp(l,r,u,d)\) 表示第 \(l\) 至第 \(r\) 个点，\(u\leq p_i\leq d\) 的子集答案。

实际上划分出的子集种类是 \(O(n^4)\) 的，因此实现的时候可以直接用二进制状态，状压点是否在集合内来表示。

转移时，沿着 \(i\) 竖着切会分为 \([l,i]\) 和 \((i,r]\) 两部分，则贡献为 \(dp(l,i,u,d)\times dp(i+1,r,u,d)\)。

但是要让这一步是 \([l,i]\) 中字典序最小的。

考虑容斥，假设这一步不是字典序最小的，设 \(\alpha\) 为实际最小字典序操作，则如果结果重复，则【\(\alpha\) 划分出来的先进行递归的点】一定属于【这一步划分出来先递归的点】。

因此记忆化搜索跑 DP，使用状压记状态，每次枚举操作 \(\alpha\)，计算划分出来的集合，判子集并减掉。

转移时需要额外维护 \(f_i\) 表示由字典序第 \(i\) 小的操作划分出的集合 \(S\) 内的点中，所有操作的字典序都大于本次操作的方案数。

具体转移如下：

int res=0;
int f[65]={};
for(int i=0;i<tmp.size();i++){
	int tres=dp(tmp[i]);
	for(int j=0;j<i;j++){
		if((tmp[j]&tmp[i])==tmp[j]){
			tres=(tres-f[j]*dp(tmp[i]^tmp[j])%mod+mod)%mod;
		}
	}
	f[i]=tres;
	tres=tres*dp(st^tmp[i])%mod;
	res=(res+tres)%mod;
}

提交记录

P10013 [集训队互测 2023] Tree Topological Order Counting 紫

题意

给定一颗 \(n\) 个点的有根树和权值序列 \(b\)。

对每个点 \(u\)，定义 \(f(u)\) 为，在所有这颗树的合法拓扑序 \(\{a\}\) 中，\(b_{a_u}\) 之和。

现在对 \(1 \le u \le n\)，求 \(f(u) \bmod 10^9+7\)。

\(n\leq 5000\)。

题解

题解写在洛谷了

上面那个链接如果不行，就点这个

提交记录

2025.6.5

The_3rd_Universal_Cup_Stage 9_Xi'an_Problem_M Random Variables *????

题意

对于一个长度为 \(n\) 取值为 \([1,m]\) 的正整数数组 \(\{a\}\)，求其中出现次数最多的数字的出现次数的期望。

题解

对出现次数最多的数字的出现次数为 \(k\) 的序列计数，这个很不好做，因此考虑容斥，令 \(f_k\) 表示出现次数最多的数字的出现次数 \(\leq k\) 的序列个数，则答案为 \(\sum\limits_{k=1}^{n} (f_k-f_{k-1})\times k\)。

考虑如何计算 \(f_k\)，本质上是 \(n\) 个不同的球放入 \(m\) 个不同的盒子，每个盒子不超过 \(k\) 个球的方案数。

这个可以 DP，枚举 \(k\)，令 \(dp_{i,j}\) 表示 \(i\) 个球放入 \(j\) 个不同的盒子，每个盒子不超过 \(k\) 个球的方案数。

初始值 \(dp_{0,j}=1\)。

则有转移方程式：

\[dp_{i,j}\leftarrow \underbrace{dp_{i-1,j}\times j}_{\text{新加入一个球，有 $j$ 个盒子可以放入}}-\underbrace{dp_{i-(k+1),j-1}\times \underbrace{\binom{i-1}{k}\times j}_{\text{选出一个盒子，再在 $i-1$ 个球中选 $k$ 个沾满这个盒子}}}_{\text{减去不合法的情况，不合法说明 $i$ 放入了一个满盒子，放入 $i$ 后盒子里有 $k+1$ 个球}} \]

最后令 \(f_k=dp_{n,m}\)。

考虑 \(dp_{n,m}\) 从 \(j\leq m\) 的哪里转移而来。

\(dp_{n,m}\leftarrow dp_{n-x\times (k+1),j-x}\times C\)。

因此当第二维度小于 \(m-\frac{n}{k+1}\) 时，这个地方的 \(dp\) 值是无效的，不会对 \(dp_{n,m}\) 产生任何贡献。

因此直接把有效状态拿出来 DP 即可，时间复杂度 \(O(\sum\limits_{k=1}^{n} \sum\limits_{i=1}^{n} \sum\limits_{j=m-\frac{n}{k+1}}^{m} 1)=O(\sum\limits_{i=1}^{n}\sum\limits_{k=1}^{n} \frac{n}{k+1})=O(n^2\ln n)\)。

提交记录

P9482 [NOI2023] 字符串 紫

题意

给定一个长度为 \(n\) 的字符串 \(s[1: n]\)。有 \(q\) 次询问，每次询问给定两个参数 \(i, r\)。你需要求出有多少 \(l\)，满足如下条件:

  • \(1 \leq l \leq r\)。
  • \(s[i: i+l-1]\) 字典序小于 \(\operatorname{Reverse}(s[i+l: i+2l-1])\)。

题解

\(F(i,j)\) 表示 \(s[i:i+2j-1]\) 是否符合条件。

则有：

\(F(i,j)=\begin{cases}0 & s_i > s_{i+2j-1} \,\cup\, j = 0 \\1 & s_i < s_{i+2j-1} \\F(i+1, j-1) & s_i = s_{i+2j-1}\end{cases}\)

扫描线算 \(F\)，对于当前 \(i\)，将 \(F(i,x)\) 看做关于 \(x\) 的函数，使用 bitset 维护这个函数。

每次往前扫的时候先将 \(F\) 左移一位，之后将 \(s_i>s_{i+2j-1}\) 的位置设为 \(0\)，将将 \(s_i<s_{i+2j-1}\) 的位置设为 \(1\)。

额外维护两只 bitset \(a_{c},b_{c}\) 分别表示当前 \(s_i>s_{i+2j-1}\) 和 \(s_i<s_{i+2j-1}\) 的位置。

需要分奇偶维护。

询问就是查 \(F(i)\) 大小为 \(r\) 的前缀中 \(1\) 的个数。

卡常，要手写 bitset。

提交记录

2025.6.6

只有一题，因为这题太恶心了做了一下午加一晚上 QAQ。

P10016 [集训队互测 2023] 虹 黑

评价：追忆 plus，炫酷卡常题。

\(19901991^2\equiv 1 \pmod {20242024}\)，所以只需要考虑指数的奇偶性即可，那么考虑 bitset。

将 \(w\) 和 \(z\) 对 \(2\) 取余，维护 bitset \(W\) 和 \(Z\)，查询 \((l,r,u)\) 时，假设 \(W=(w_1,w_2,\dots w_n)\)，\(Z=(z_{\gcd(u,1)},z_{\gcd(u,2)},\dots z_{\gcd(u,n)})\)，设 \(C\) 为 \(W\operatorname{AND} Z\) 中 \([l,r]\) 间 \(1\) 的个数，则答案为 \(19901991\times C+1\times (r-l+1-C)\)。

如何算 \(W\)

维护 \(W_i\) 表示在第 \(i\) 次操作后 \(w\) 的 bitset，由于我们只关心奇偶性，因此一开始令 \(W_i\) 为这次操作修改的位置集合，最后做一遍前缀异或和即可。

考虑分块求每次修改的位置集合。

首先 \([l,r]\) 的最小虹就是每个点到根的路径并集除去 \([l,r]\) 中所有点 \(\operatorname{lca}\) 的父亲到根的路径，先不管所有点 \(\operatorname{lca}\) 的父亲到根的路径，考虑如何求 \([l,r]\) 到根的路径并。

由于数据随机，所以当 \(l,r\) 在同一块内时直接 \(O(n)\) 暴力即可。

否则拆成整块和散块，离线处理。

预处理 \(blk_i\) 表示第 \(i\) 块的最小虹集合，枚举每个点并往上跳，跳到已经访问过的节点就停止，代码大概长这样：

for(int i=1;i<=n;i++){
	int u=i;
	while(u){
		if(blk[id[i]].test(u)) break;
		blk[id[i]].set(u);
		u=f[u][0];
	}
}

离线后散块同样暴力处理，第一次遇到分块上这种离线查询，贴个代码：

vector<int> qryblk[305][305],qrypre[80005],qrysuf[80005],qryup[80005];
void dfsW(int u,int fa){//这里下面讲
	for(int x:qryup[u]) W[x]^=w;
	for(int v:V[u]){
		if(v==fa) continue;
		w.set(v,1);
		dfsW(v,u);
		w.set(v,0);
	}
}
void initW(){
	for(int i=1;i<=tot;i++){
		w.reset();
		for(int j=i;j<=tot;j++){
			w|=blk[j];
			for(int x:qryblk[i][j]) W[x]|=w;
		}
	}
	for(int i=1;i<=tot;i++){
		w.reset();
		for(int j=L[i];j<=R[i];j++){
			int u=j;
			while(u){
				if(w.test(u)) break;
				w.set(u);
				u=f[u][0];
			}
			for(int x:qrypre[j]) W[x]|=w;
		}
	}
	for(int i=1;i<=tot;i++){
		w.reset();
		for(int j=R[i];j>=L[i];j--){
			int u=j;
			while(u){
				if(w.test(u)) break;
				w.set(u);
				u=f[u][0];
			}
			for(int x:qrysuf[j]) W[x]|=w;
		}
	}
	w.reset();
	w.set(1,1);
	dfsW(1,0);//这里下面讲
	w.set(1,0);
}

然后考虑 \([l,r]\) 中所有点 \(\operatorname{lca}\) 的父亲到根的路径怎么去掉，设所有点 \(\operatorname{lca}\) 的父亲到根的路径的点集合 \(X\)，则让对应的 \(W\) 异或上 \(X\) 即可。

首先要求出 \([l,r]\) 中所有点的 \(\operatorname{lca}\)，这个可以计算相邻 \(\operatorname{lca}\) 后用 ST 表取深度最小的点来做。

然后把这个操作也离线下来，最后做一遍 dfs 即可（代码在上面）。

如何算 \(Z\)

给出一个十分暴力的代码：

int g[80005];
void brute(int now,int lst,int pw){
	for(auto x:qry[now]){
		int c=calc(x.l,x.r,x.t);//calc 表示处理当前询问。
		ans[x.t]=(1ll*c*19901991+x.r-x.l+1-c+20242024)%20242024;
	}
	for(int i=lst;i<=cnt;i++){
		if(1ll*now*pri[i]>n) break;
		int t=now*pri[i];
		int npw=pri[i];
		if(i==lst) npw*=pw;
		for(int j=npw;j<=n;j+=npw){
			g[j]*=pri[i];
			Z.set(j,z[g[j]]&1);
		}
		brute(t,i,npw);
		for(int j=npw;j<=n;j+=npw){
			g[j]/=pri[i];
			Z.set(j,z[g[j]]&1);
		}
	}
}

发现在 \(n=80000\) 时计算量大概在 \(4\times 10^7\) 左右。

大概就是暴搜一个数的质因子组成，实时维护 \(Z\)，每次增加一个质因子。假如将质因子 \(p^c\) 增加为 \(p^{c+1}\)，则所有是 \(p_{c+1}\) 倍数的数与当前数的 \(\gcd\) 都会乘上 \(p\)。

如何处理询问

求 \(Z\) 时处理询问，直接把两个 bitset 与起来求 \([l,r]\) 之间的 popcount 即可。这里使用了手写 bitset。

int calc(int l,int r,int t){//这里的小写 w 指上文中的 Z。
	int B=64;
	int idxl=l/B,idxr=r/B;
	int reml=l&(B-1),remr=r&(B-1);
	int res=0;
	if(idxl==idxr){
		res=__builtin_popcountll(W[t].bits[idxl]&w.bits[idxr]&(~0ull<<reml)&(~0ull>>(63-remr)));
		return res;
	}
	res+=__builtin_popcountll(W[t].bits[idxl]&w.bits[idxl]&(~0ull<<reml));
	for(int i=idxl+1;i<=idxr-1;i++){
		res+=__builtin_popcountll(W[t].bits[i]&w.bits[i]);
	}
	res+=__builtin_popcountll(W[t].bits[idxr]&w.bits[idxr]&(~0ull>>(63-remr)));
	return res;
}
闲话

洛谷评测机跑的很快，不做任何卡常即可通过，但本题在 qoj 和 vjudge 上极度卡常，需要用快速读入+手写 bitset。

在洛谷的提交记录

在 qoj 加上快读卡常的提交记录

2025.6.7

咕咕咕

2025.6.8

P8861 线段 黑

题意

有一个初始为空的线段集，你需要处理 \(q\) 组询问，每组询问的格式为如下三种之一：

  1. 加入一条新线段 \([l_i,r_i]\)。
  2. 将线段集里所有与 \([l_i,r_i]\) 相交的线段修改为其与 \([l_i,r_i]\) 的交。
  3. 求出线段集里所有与 \([l_i,r_i]\) 相交的线段与 \([l_i,r_i]\) 的交的长度和。

强制在线。

题解

首先假设没有操作 \(2\)。

那么可以使用树状数组处理。

具体地，维护四颗权值树状数组，分别表示 \(\sum [l=i],\sum i\times [l=i],\sum [r=i],\sum i\times [r=i]\)。

那么假设查询区间是 \([l,r]\)，我们需要求：

\[\sum_{[L,R]}\bigl|[L,R]\cap[l,r]\bigr|=\sum_{\text{交}}\bigl(\min(R,r)-\max(L,l)\bigr) \]

那么考虑求出 \(\sum min(R,r)\) 和 \(\sum -max(L,l)\)，再把不相交区间多算的部分减掉。

这部分代码：

void addl(int l,int v){
	bitl.add(l,v);
	bitlx.add(l,v*l);
}
void addr(int r,int v){
	bitr.add(r,v);
	bitrx.add(r,v*r);
}
int query(int l,int r){
	//min(R,r)-max(L,l)
	int res=0;
	//\sum min(R,r)
	res+=bitrx.sum(r)+r*(bitr.sum(n)-bitr.sum(r));
	//\sum -max(L,l)
	res-=bitlx.sum(n)-bitlx.sum(l)+l*bitl.sum(l);
	//左侧负贡献\sum_{R<l} R-l 
	res-=bitrx.sum(l-1)-l*bitr.sum(l-1);
	//右侧\sum_{L>r} r-L 
	res-=r*(bitl.sum(n)-bitl.sum(r))-(bitlx.sum(n)-bitlx.sum(r));
	return res;
}

然后发现 \(l\) 和 \(r\) 对答案贡献其实是独立的。

接下来考虑维护操作二。

subtask 5 启示我们使用猫树分治，把区间 \([l,r]\) 拍到满足 \(L\leq l\leq mid<r\leq R\) 的线段树节点上。

每个节点开一个小根堆和一个大根堆，分别维护左端点和右端点。

同时用数组记录每对左端点和右端点的匹配关系，这个修改要用。使用两个并查集分别缩掉左端点和右端点相同的节点，这样可以做到修改均摊。

加入是简单的。

修改 \([l,r]\) 时，按如下操作遍历：

  • \([l,r]\) 与 \([L,R]\) 无交集，或 \([L,R]\in [l,r]\)，直接返回。

  • \(L\leq l\leq mid<r\leq R\)。

    • 左右端点分别对 \(l,r\) 取 \(\max,\min\)，直接用堆暴力做，然后并查集缩点保证复杂度。

  • \(r\leq mid\)。

    • 不断 pop 堆中元素直到 \(l'>r\)，找出 \(l'\leq r\) 的所有区间，暴力下放到左子树即可。

  • \(l>mid\)，与 \(r\leq mid\) 同理。

堆中还要维护所对应并查集的根节点，即堆维护的是一个 pair。

放一个修改代码：

void ins(int p,int l,int r,int u,int x){
	if(bvld[u]){
		int v=mch[u];
		bvld[u]=bvld[v]=0;
		int L=min(x,val[fd(v)]),R=max(x,val[fd(v)]);
		sz[fd(u)]--,sz[fd(v)]--;
		int newl=max(L,l),newr=min(R,r);
		addl(L,-1);
		addr(R,-1);
		if(newl!=newr){
			addl(newl,1);
			addr(newr,1);
			insert(p,newl,newr);//insert是操作一插入区间的函数。
		}
	}
	for(int v:V[u]) ins(p,l,r,v,x);
}
void modify(int p,int l,int r){
	if(l<=t[p].l&&t[p].r<=r) return;
	int mid=(t[p].l+t[p].r)/2;
	if(r<=mid){
		while(!t[p].ql.empty()){
			auto x=t[p].ql.top();
			if(x.first>r) break;
			t[p].ql.pop();
			ins(p*2,l,r,x.second,x.first);
		}
		modify(p*2,l,r);
	}else if(l>mid){
		while(!t[p].qr.empty()){
			auto x=t[p].qr.top();
			if(x.first<l) break;
			t[p].qr.pop();
			ins(p*2+1,l,r,x.second,x.first);
		}
		modify(p*2+1,l,r);
	}else{
		int newrt=0;
		while(!t[p].ql.empty()){
			auto x=t[p].ql.top();
			if(x.first>=l) break;
			t[p].ql.pop();
			addl(x.first,-sz[x.second]);
			newrt=merge(newrt,x.second);
		}
		if(newrt){
			val[newrt]=l;
			addl(l,sz[newrt]);
			t[p].ql.push({l,newrt});
		}
		newrt=0;
		while(!t[p].qr.empty()){
			auto x=t[p].qr.top();
			if(x.first<=r) break;
			t[p].qr.pop();
			addr(x.first,-sz[x.second]);
			newrt=merge(newrt,x.second); 
		}
		if(newrt){
			val[newrt]=r;
			addr(r,sz[newrt]);
			t[p].qr.push({r,newrt});
		}
		modify(p*2,l,r);
		modify(p*2+1,l,r);
	}
}

查询调 query 就行了。

提交记录

P11236 [KTSC 2024 R1] 水果游戏 黑

题意

给定一个长度 \(n(n\leq 10^5)\) 的序列 A，每个数字代表水果等级。
一次合并操作可以把相邻且数值相同的两个水果合成更大的一个（数值 +1）。
在 \(q(q\leq 10^5)\) 次在线操作中，需要支持：

  1. 区间查询 play_game(l,r)
    ─ 返回区间 A[l…r] 经过任意次合并后能得到的最大水果等级。
  2. 单点修改 update_game(p,v)
    ─ 把位置 p 处的水果替换为等级 v (1…10)。

题解

考虑没有修改怎么做。

先缩连续段，表示成 \(\{(val_1,cnt_1),(val_2,cnt_2),\dots\}\)。

其中 \((val,cnt)\) 表示 \(val\) 连续出现 \(cnt\) 次。

考虑一个谷结构，即 \(val_1>val_2<val_3\)。

那么需要让 \(val_2\) 提升到 \(\min\{val_1,val_3\}\)，设 \(d=\min\{val_1,val_3\}-val_2\)，如果 \(cnt_2\) 不是 \(2^d\) 的倍数，说明中间一定有数字够不到 \(\min\{val_1,val_3\}\)，因此这个段会断开，分成两个子问题。

因为是相邻合并，考虑维护一个栈结构，末尾不断消除谷结构，直到不存在谷后将当前节点入栈。

为了保证节点数 \(O(V)\)，每次遇到段会断开的情况，就将 \((+\infin,1)\) 入栈，前面递减的部分就因为谷结构一次性被消除，最后序列里只剩下开头的递增部分和结尾的递减部分。

可以使用递归实现栈结构的维护。

void push_back(int val,int cnt){
	if(!cnt) return;
	while(tot>=2&&a[tot-1].val>a[tot].val&&a[tot].val<val){
		int v=a[tot].val,c=a[tot].cnt;
		tot--;
		if(a[tot].val==inf&&val==inf) continue;
		int d=min(val,a[tot].val)-v;
		push_back(v+d,c>>d);
		if(c&((1<<d)-1)){
			push_back(inf,1);
			push_back(v+d,c>>d);
		}
	}
	if(!tot) a[++tot]={val,cnt};
	else if(a[tot].val==val) a[tot].cnt+=cnt;
	else a[++tot]={val,cnt};
	if(a[tot].val<inf){
		res=max(res,a[tot].val+__lg(a[tot].cnt));
	}
}

然后发现加入元素的过程中，栈里面最多有一个单峰的东西，点个数 \(O(V)\)，因此直接丢到线段树上，查询时暴力合并即可。

//暴力合并
node operator+ (const node &b) const{
	node c;
	c.res=max(res,b.res);
	for(int i=1;i<=tot;i++){
		c.push_back(a[i].val,a[i].cnt);
	}
	for(int i=1;i<=b.tot;i++){
		c.push_back(b.a[i].val,b.a[i].cnt); 
	}
	return c;
}

查询时需要在两边加上 \((+\infin,1)\)，这样就可以消除完所有节点，保证答案更新彻底。

int play_game(int l,int r){
	tmp=newnode(inf)+query(1,l,r)+newnode(inf);
	return tmp.res;
}

提交记录

P6261 [ICPC 2019 WF] Traffic Blights 黑

题意

街道上有 \(n\) 个红绿灯，第 \(i\) 个灯距离街道最西端 \(x_i\) 米，以【持续 \(r_i\) 秒的红灯，再持续 \(g_i\) 秒的绿灯】作为一周期，不断重复。在时刻 \(0\)，所有的红绿灯都恰好刚变为红灯。

有一辆汽车在随机时刻出现在了街道最西端，向东以 \(1~ \rm m/s\) 龟速行驶，直到遇到第一个红灯时停下，求：

  • 它有多大的概率通过所有红绿灯？
  • 如果它停下来了，它在每个红绿灯处停下的概率有多大？

\(1\leq n\leq 500,1\leq r+g\leq 100,q\leq x\leq 10^5\)

题解

设 \(p_i\) 表示通过前 \(i\) 个灯的概率，则在第 \(i\) 个灯停下的概率为 \(p_{i-1}-p_{i}\)。

街道周期为 \(M=\operatorname{lcm}_{i=1}^{n} (r_i+g_i)\)，题目等价于求 \([0,M-1]\) 内随机一个整数，通过前 \(i\) 个灯的概率。

假设开始时间为 \(X\)，则能通过前 \(i\) 个灯，当且仅当：\(\forall_{1\leq j\leq i}(X+x_j)\bmod (r_j+g_j)\geq r_j\)。

特殊情况

考虑特殊情况，假设 \((r_i+g_i)\) 全部互质。

根据中国剩余定理，任何模数互质的同余方程组在周期内有唯一解，即：

给定任何剩余序列

\[a_1,\dots ,a_n,\qquad 0\le a_i<T_i, \]

总存在 唯一 的

\[X\in[0,M) \]

使得

\[(X+x_i)\equiv a_i\pmod{T_i}\qquad(\forall i). \]

也就是说 \((X+x_i)\bmod (r_i+g_i)\) 构成的序列与开始时间 \(X\) 一一对应，所以每项算概率可以独立算，通过前 \(i\) 个灯的概率为 \(\prod\limits_{j=1}^{i} \frac{g_j}{r_j+g_j}\)。

一般情况

取 \(V=2520\)，把开始时间 \(X\) 表示成 \(kV+b\)，那么枚举 \(b\)，设 \(k\) 是变量，根据经典结论，\(b\) 每次增加 \(V\)，模 \(r_i+g_i\) 的周期为 \(\frac{r_i+g_i}{\gcd(r_i+g_i,V)}\)。

发现 \(0\sim 100\) 中的每个数 \(v\)，都满足 \(\frac{v}{\gcd(v,V)}\) 是一个质数的若干次幂，则可以把周期底数相同的灯看做一个等价类，每个等价类中的灯周期向该类中最长周期对齐（其实就是直接按最长周期算）。

算的时候，不同周期之间是独立的，可以分别计算。

维护 \(stop_{i,j}\) 表示在 \(j\bmod i\) 时刻开始会不会被周期为 \(i\) 的灯拦下，然后枚举模周期的余数，用古典概型计算概率即可。

代码中的 now 可以类比特殊情况的 \(\prod\limits_{j=1}^{i} \frac{g_j}{r_j+g_j}\)（只是类比好理解，其实公式完全不同）。

void calc(int b){
	memset(stop,0,sizeof(stop));
	p[0]++;
	double now=1;
	for(int i=1;i<=n;i++){
		int d=m[i]/__gcd(V,m[i]);
		int M=mx(d);
		int cnt=0,tot=0;
		for(int j=0;j<M;j++){
			if(stop[M][j]) continue;
			if(pass[i][(j*V+b)%m[i]]){
				cnt++;
			}else{
				stop[M][j]=1;
			}
			tot++;
		}
		if(!tot) break;
		now=now*cnt/tot;
		p[i]+=now;
	}
}

提交记录

2025.6.9

P12734 理解 蓝

题意

有 \(n\) 个历史事件，每个事件可能依赖一个编号更小的前置事件（\(p_i<i\)，若 \(p_i=0\) 则无前置）。现在有 \(m\) 个题目，每个题目要求你记起特定的事件。

你可以通过：

  • 回想（直接记起事件 \(u\)，耗时 \(r_u\)）；
  • 联想（从已记起的事件 \(p_v\) 联想到其后继 \(v\)，耗时 \(t_v\)）来记起事件。
  • 忘记（忘掉一个事件）。

记忆容量限制为最多同时记起 \(k\) 个事件。事件一旦忘记，就不能再重新记起。

求记起 \(m\) 个事件的最小时间（不要求同时记起来，只要求 \(m\) 个事件都被记起过即可）。

\(n\leq 10^5,k\leq 10\)。

题解

回想节点 \(i\) 并向下联想，联想出来的点是一个连通快，删去连通块后原问题划分为若干个子问题，因此考虑树形 DP。

状态

令 \(f_{i,j}\) 表示 \(i\) 为根的子树，可以向下联想最多 \(j-1\) 个事件，不考虑 \(i\) 的贡献，解决子树内所有题目的最小时间。

特别的，\(f_{i,0}\) 表示不回想 \(i\)，\(f_{i,1}\) 表示回想了 \(i\)，但不往下联想。

答案

将 \(0\) 号点连向所有的根，令 \(r_0=+\infin\)，最终答案为 \(f_{0,0}\)。

初值

初始时对于叶子节点 \(u\)，\(f_{u,x}=0\ (x\geq 1)\)。若 \(u\) 是一道题目要求的事件，则 \(f_{u,0}=+\infin\)，否则 \(f_{u,0}=0\)。

转移

先考虑特殊的 \(f_{u,0}\)，若 \(u\) 是一道题目要求的事件，则 \(f_{u,0}=+\infin\)，否则 \(f_{u,0}=\sum\limits_{v\in u} \min\{f_{v,0},f_{v,k}+r_v\}\)，表示对下面的点是否被回想进行决策。

考虑特殊的 \(f_{u,1}\)，和 \(f_{u,0}\) 一样都不能对下面节点造成影响，唯一区别是不用考虑若 \(u\) 是否是题目要求的事件，\(f_{u,1}=\sum\limits_{v\in u} \min\{f_{v,0},f_{v,k}+r_v\}\)。

考虑 \(f_{u,x}\ (x\geq 2)\)，转移大概是选一个儿子 \(v0\)，先解决其他儿子后再联想 \(v0\)，并忘掉父亲。

令

\[a_{v,x}\;=\;\min\!\Bigl(\,\min\!\bigl(f_{v,0},\;f_{v,k}+r_v\bigr),\;f_{v,x-1}+t_v\Bigr), \qquad b_{v,x}\;=\;f_{v,x}+t_v. \]

\(a_{v,x}\) 表示不忘父亲继续往下联想，\(b_{v,x}\) 表示忘掉父亲。

则有：

\[\boxed{ f_{u,x}\;=\; \sum_{v\in V_u} a_{v,x}\;+\; \min\!\Bigl(0,\;\min_{v\in V_u} (b_{v,x}-a_{v,x})\Bigr) }. \]

提交记录

P12607 三叉求和 紫

题意

有一棵深度无穷大的以 \(0\) 为根的三叉树，节点 \(i\) 的儿子分别是节点 \(3i+1,3i+2,3i+3\)。

设节点 \(i\) 的点权为 \(a_i\)。对于 \(0\le j\le 2\)，有 \(a_{3i+j+1}=3\times a_i+j\)，特别的，\(a_0=0\)。

你的任务是求从根出发，找长度 \(=d\) 的简单路径，并使得该路径经过的所有点的点权和为 \(k\)。你需要求出所有合法路径的条数。

然而 \(k\) 并不唯一，\(k\) 的三进制表示中仅有某些位是已知的，而其它的位将以字符 \(\tt ?\) 表示。你需要对所有可能的 \(k\) 在上述问题中的答案求和，最后再对 \(10^9+7\) 取模。

题解

设序列 \(\{b\}\)，\(b_i\in \{0,1,2\}\)，表示第 \(i\) 次向那个方向走。

重新定义题目中的序列 \(\{a\}\)，\(a_i\) 表示走完第 \(i\) 步到达的节点点权。

则 \(a_i=\sum\limits_{j=1}^{i} b_j\times 3^{i-j}\)。

题目要求 \(\sum\limits_{i=1}^{d} a_i=k\)，即 \(\sum\limits_{i=1}^{d} \sum\limits_{j=1}^{i} b_j\times 3^{i-j}=k\)。

\(b_i\) 的系数是 \(3\) 的若干次方，这个式子看着就很数位 DP，把 \(b_i\) 的贡献按照系数分类。

\[\sum\limits_{i=1}^{d} \sum\limits_{j=1}^{i} b_j\times 3^{i-j} \\ =\sum_{x=0}^{d} \sum_{i=1}^{d} \sum_{j=1}^i\ [i-j=x]\times 3^x\times b_j \\ 发现此时 i 没有用处，只用限制 1\leq i=j+x\leq d 即可。 \\ 原式=\sum_{x=0}^{d} \sum_{j=1}^{d-x} 3^x\times b_{j} \\ =\sum_{x=0}^{d} 3^x\times \sum_{j=1}^{d-x} b_{j} \\ 记 s_i=\sum_{j=1}^{d-i} b_j \\ 原式=\sum_{x=0}^{d} 3^x\times s_x \]

那么对 \(s\) 进行三进制数位 DP，由于 \(s_d=0\)，故从高位开始，\(f_{pos,lst,up}\) 表示高 \(pos-1\) 位已确定，\(s_{pos-1}=j\)，这一位需要向上进位 \(up\)，剩余未确定位置的方案数。

答案和初值是显然的。

转移为 \(f_{pos,lst,up}=\sum\limits_{x=0}^2 f_{pos+1,lst+x,3\times up+now-(lst+x)}\)。

其中，\(now\) 表示 \(k\) 这一位的数字，当 \(k\) 这一位为 ? 时，枚举 \(now=0,1,2\) 即可。

我们得到了 \(O(n^3)\) 做法，但是题目要求 \(O(n^2)\)。

我们充分发扬人类智慧，使用递推实现转移，然后猜测 \(f_{pos,lst,*}\) 只有 \(O(1)\) 个接近的非 \(0\) 位置，维护 \(l_{pos,lst},r_{pos,lst}\) 表示非 \(0\) 区间的左右端点，只转移非 \(0\) 位置即可。

本地测试极限数据（全为 ?）大概 0.6 秒，复杂度 \(O(能过)\)

提交记录

P3195 [HNOI2008] 玩具装箱 紫

发现以前学斜率优化没写这题，刚好复习一下。

题意

标准序列划分问题，区间 \([i,j]\) 的贡献为 \(\big(j-i+(\sum\limits_{k=i}^{j} C_k)-L\big)^2\)。

题解

令 \(S_i=i+\sum\limits_{j=1}^i C_j\)，\(f_i\) 表示前 \(i\) 项以 \(i\) 结尾的答案，\(L'=L+1\)。

易得：

\[f_i=\min\limits_{j=0}^{i-1} \{f_j-2 S_i S_j+S_j^2+2S_jL'\}+S_i^2-2 S_i L'+L'^2。 \]

令 \(X(i)=S_i,Y(i)=S_i^2+2 S_i L'+f_i,K(i)=2\times S_i,B(i)=f_i,C(i)=S_i^2-2 S_i L'+L'^2\)，则有：

\[f_i=\min\limits_{j=0}^{i-1} \{Y(j)-K(i)\times X(j)\}+C(i) \]

斜率优化即可。

P2305 [NOI2014] 购票 黑

题意

给你一棵树，每个点有三个系数 \(l,p,q\) 表示你能选择一个点 \(v\)，满足 \(v\) 是当前点的 \(d(d\leq l)\) 级祖先，花费 \(d\times p+q\) 元到达 \(v\)。

求每个点到 \(1\) 的最短路，\(n\leq 10^5\)。

题解

令 \(fa^k_i\) 表示 \(i\) 的 \(k\) 级祖先，\(g_i\) 表示 \(i\) 到根的最短路，则有：

\[g_i=\min_{d=1}^{l_i} \{g_{fa^k_i}+d\times p_i+q_i\} \]

然后考虑链的部分分，把 \(d\) 拆成到根距离相减的形式，然后斜率优化即可。

最后考虑树，使用点分治优化，处理子树 \(u\) 时，为了保证转移顺序正确：

  1. 找到重心 \(rt\) 后，先递归处理包含 \(u\) 的子树
  2. 然后处理 \(rt\) 到 \(u\) 的链这一段对不包含 \(u\) 的子树的转移
  3. 最后递归处理不包含 \(u\) 的子树。

特别的，把 \(rt\) 视为包含 \(u\) 的子树中的一个节点。

先推斜率优化式子，\(dis_i\) 表示 \(i\) 到根的距离。

\[g_i=\min_{j} \{g_j+d\times p_i+q_i\} \\ g_i=\min_{j} \{g_j-dis_j\times p_i\}+dis_i\times p_i+q_i \]

然后就可以维护一个斜率优化队列了。

处理第二步的时候往下把这个子树所有点搜出来，按能到达的最小深度 \(dis_i-l_i\) 降序排序，之后类似扫描线，扫到 \(i\) 时，让 \(rt\) 不断往父亲跳，记挑到的点是 \(now\)，满足 \(dis_i-l_i\leq dis_{now}\)，然后把 \(now\) 丢到队列里即可。

点分治内有排序，时间复杂度 \(O(n\log^2 n)\)。

提交记录

2025.6.10

P3381 【模板】最小费用最大流 模版

学习费用流。

提交记录

P2756 飞行员配对方案问题 绿

板刷网络流与线性规划 24 题。

二分图匹配模版。

提交记录

P4016 负载平衡问题 蓝

板刷网络流与线性规划 24 题。

增加原点 \(s\)，汇点 \(t\)，把原运输图每条边连上流量为 \(+\infin\)、价格为 \(1\) 的边，原点向大于平均值的点连流量为【与平均值的差】、价格 \(0\) 的边，汇点向小于平均值的点连流量为【与平均值的差】、价格 \(0\) 的边。

然后跑最小费用最大流即可。

提交记录

P4014 分配问题 蓝

建出二分图匹配模型，跑最（小/大）费用最大流即可。

提交记录

P4015 运输问题 蓝

与上题相同

提交记录

网络流题单前面的题都比较简单，直接贴题号了

P3254 提交记录

P3355 提交记录

2025.6.11

P2763 提交记录

P2765 魔术球问题 蓝

对于相加是平方数的数对，小数向大数连边，构成一个 DAG。

每次加入一个球，求 DAG 的最小路径覆盖是否 \(\leq n\) 即可。

将原图每个顶点拆分为出点 \(pi'\) 和入点 \(pi''\)，原图的边 \(pi\to pj\) 转化为二分图中 \(pi'\) 与 \(pj''\) 的边‌。

则有：最小路径覆盖数 = 原图顶点数 - 二分图最大匹配数‌。

提交记录

P1251 餐巾计划问题 紫

标准网络流建模。

建模方法：

//源汇点，商店
shop=2*N+1,S=2*N+2,T=2*N+3;
mcmf.add(S,shop,inf,0);
//回收点 1~N
for(int i=1;i<=N;i++) mcmf.add(S,i,r[i],0);
//提供点&传送链 N+1~2N
mcmf.add(shop,N+1,inf,p); 
for(int i=2;i<=N;i++) mcmf.add(N+i-1,N+i,inf,0);
for(int i=1;i<=N;i++){
	if(i+m<=N) mcmf.add(i,N+i+m,inf,f);
	if(i+n<=N) mcmf.add(i,N+i+n,inf,s);
}
for(int i=1;i<=N;i++) mcmf.add(N+i,T,r[i],0);

提交记录

CF2046D For the Emperor! *3100

题意

给定一个 有向图，包含 \(n\) 个点和 \(m\) 条边。第 \(i\) 个点上有 \(a_i\) 个人。

你可以选择一些结点发放一份计划，接下来每个人可以沿着边自由移动，如果一个人从一个收到过计划的点移动到一个没有收到计划的点，那么可以令其收到计划。

你需要让所有的点都收到计划，求最少需要在多少个结点发放计划，或者报告无解。

\(a_i\leq n\leq 200,m\leq 800\)。

题解

先缩点变成 DAG，问题与原问题等价。

构造费用流模型：令 \(B\to +\infin\)，经过所有点很难用最大流刻画，因此我们的思路是：保证最大流总是能取到的情况下，经过一个点的费用是 \(-B\)，发放一个计划的代价是 \(1\)。这样求出最小费用后再模 \(B\) 就是我们想要的费用。

套路的将 DAG 拆点，先把图中的边连 \(u\to v\) 上，出点 \(P_u\) 连入点 \(Q_v\)，点 \(u\) 被经过可以刻画为经过边 \(P_u\to Q_u\)。

然后我们设保证能取到的最大流为 \(\sum a_i\)，我们建立约束点 \(F_u\)，建边 \(s\to_{(a_u,0)} F_u\)，建边 \(Q_u\to_{(+\infin,0)} T\)。

为了保证只有一个点第一次经过才被计费，这样建边：\(P_u\to Q_u\) 连两条边，一条 \((1,1)\)，一条 \((+\infin,0)\)。

然后让 \(F_u\) 提供一个人给 \(P_u\) 来复制计划，剩余全给 \(Q_u\)。即 \(F_u\to_{(1,1)} P_u\)，\(f_u\to_{+\infin,0} Q_u\)。

跑最小费用最大流，完结散花 QwQ。

提交记录

AT_abc397_g [ABC397G] Maximize Distance 紫

题意

给定一个包含 \(N\) 个顶点和 \(M\) 条边的有向图。顶点编号为 \(1,2,\dots,N\)，其中第 \(j\) 条边（\(j=1,2,\dots,M\)）从顶点 \(u_j\) 指向顶点 \(v_j\)。保证从顶点 \(1\) 到顶点 \(N\) 是可达的。

初始时，所有边的权重均为 \(0\)。当从 \(M\) 条边中恰好选择 \(K\) 条边并将其权重改为 \(1\) 时，求修改后的图中顶点 \(1\) 到顶点 \(N\) 的最短距离的最大可能值。

\(N\leq 30\)，\(K\leq M\leq 100\)。

题解

二分答案，求令最短路 \(=d\) 时最少改几条边。

当 \(d=1\) 时是最小割问题。

当 \(d\neq 1\) 时，令 \(dis_i\) 表示 \(1\) 到 \(i\) 的距离，相当与给每个 \(dis_i\) 赋值，满足三角不等式，且如果存在边 \(u\to v\)，满足 \(dis_v=dis_u+1\)，需要支付 \(1\) 费用。

拆点，每个 \(dis_u\) 拆成 \(b_{u,1}\sim b_{u,d}\)，\(b_{u,x}=[dis_{u} \leq x]\)。

则有限制：

  • 如果 \(b_{i,j}=0\)，则 \(b_{i,j+1}\neq 1\)。
  • 对于边 \(u\to v\)，如果这条边有贡献，当且仅当 \(b_{u,j}=0,b_{u,j-1}=1,b_{v,j}=1\)。
  • \(b_{1,0}=1,b_{n,d-1}=0\)。

因此按照如下方式连边跑最小割：

  • \(b_{i,j}\to_{+\infin} b_{i,j+1}\)。
  • \(b_{u,j}\to_{1} b_{v,j}\)，\(b_{u,j}\to_{+\infin} b_{u,j+1}\)。
  • \(S\to_{0} b_{1,0},T\to_{0} b_{n,d-1}\)。

实现时直接令 \(S=b_{1,0},T=b_{n,d-1}\) 即可。

提交记录

2025.6.12

Express Eviction *????

题意

在 \(N\times M\) 的网格中，有若干障碍，每个障碍在四个格点组成的方格中，一个障碍可以 ban 掉周围四个

格点，你要在格点上行走，从 \((0,0)\) 走到 \((N,M)\)，最少移除多少障碍？

题解

考虑最小点割，如果两个障碍的 \(x,y\) 坐标都相差不超过 \(2\)，那么两个障碍会把之间的格点 ban 掉，所以新建左下和右上各 \(N+M\) 个虚点，把相差不超过 \(2\) 的障碍连边，相当于最少移除几个障碍使得左下到不了右上，因此跑最小点割即可。

最小点割的做法为将一个点拆为入点 \(in(i)\) 和出点 \(out(i)\)，连接 \(in(i)\to out(i)\) 流量为删掉这个点的代价（对于本题，虚点为 \(+\infin\)，图上障碍为 \(1\)）。对于图上边 \((u,v)\)，连接 \(out(u)\to in(v)\)，流量为 \(+\infin\)。

提交记录

[ARC142E] Pairing Wizards 黑

题意

有 \(n\) 个巫师，第 \(i\) 个巫师有 \(a_i\) 的法力并计划打败 \(b_i\) 法力的怪兽。

构造 \(\{A_n\}\)，使得对于给定的 \(m\) 组 \((x, y)\)，均有 \(A_x \geq b_x, A_y \geq b_y\) 或 \(A_y \geq b_x, A_x \geq b_y\)。

请最小化 \(\sum\limits_{i=1}^n |A_i - a_i|\)。

题解

先对于所有 \((x,y)\)，把 \(a_x,a_y\) 向 \(\min\{b_x,b_y\}\) chkmin，然后限制转化为 \(a_x\geq \max\{b_x,b_y\} \lor a_y\geq \max\{b_x,b_y\}\)，下文中的 \(a_i\) 指 chkmin 完的 \(a_i\)。

考虑最小割。

把第 \(i\) 点拆为 \(V-a_i+1\) 个点：\(c_{i,0},c_{i,1},\dots,c_{i,V-a_i}\)。其中 \(c_{i,j}\) 向 \(c_{i,j-1}\) 连流量为 \(+\infin\) 的边，\(c_{i,j}(j>0)\) 向 \(T\) 连接流量为 \(1\) 的边。

让 \(a_i\) 增加 \(k\)，可以刻画为强制让 \(c_{i,k}\) 无法到达 \(T\)，这样需要割掉 \(c_{i,1\sim k}\) 向 \(T\) 的连边。

考虑限制 \(a_x\geq z\lor a_y\geq z\)，可以让 \(S\) 向 \(c_{y,z-a_y}\) 连接 \(z-a_x\) 的边，则要么割掉 \(z-a_x\) 边，表示将 \(a_x\) 上调至 \(z\)，要么割 \(c_{y,1\sim z-a_y}\) 的所有边，表示将 \(a_y\) 上调至 \(z\)。

但是这样会有问题，对于限制 \((x,y_1)\)，\((x,y_2)\)，\(S\) 会向外连接两条调整 \(a_x\) 的边，它们如果都被割掉，就算重了。

那么考虑固定一条边的边权。

具体地，假设 \(b_x\leq b_y\)，连接 \(S\to c_{y,0}\)，边权为 \(b_y-a_y\)，连接 \(c_{y,0}\to c_{x,b_y-a_x}\)，边权为 \(+\infin\)。

这种效果和上面建模的效果相同，但是注意到 \(S\to c_{y,0}\) 的边权只有 \(1\) 种，所以可以通过只保留若干 \(S\to c_{y,0}\) 边中的一条边，来实现去重。

建完图跑最小可就行了。

提交记录

CF1427G One Billion Shades of Grey *3300

题意

给定一个 \(n \times n\) 的棋盘，其边界上所有位置均填好了数字，你需要在剩余 \((n-2) \times (n-2)\) 个位置上填数，部分位置已经“破损”，在输入时用 \(-1\) 描述，此处无法填数。

对于一种填数方案，定义一对相邻（四连通）的均不为“破损”的格子的贡献为其填入的数字的差值的绝对值，定义此填数方案的权值为各个相邻的格子的贡献之和。

你需要最小化权值，输出可以得到的最小权值。

\(3\leq n\leq 200\)。

题解

如果边上的点都是 \(1,2\)，可以连边跑最小割。

一般情况下，\(v_r-v_l=(v_r-v_{r-1})+(v_{r-1}-v_{r-2})+\cdots +(v_{l+1}-v_l)\)。

然后枚举 \(v_i\)，把 \(\leq v_i\) 的连向 \(S\)，把 \(>v_i\) 的连向 \(T\)，求得最大流 \(f\)，对答案产生的贡献为 \(f\times (v_{i+1}-v_i)\)。

相当于每次删一条边，在加一条边，求最大流。使用退流技巧即可。

提交记录

2025.6.13

Knights of Night *????

题意

给定一张二分完全图去掉 \(m\) 条边，剩下的边满足 \(u, v\) 之间的边权为 \((a_u + a_v) \bmod 998244353\)。

对于 \(1 \leq i \leq k\) 的所有 \(i\)，求匹配 \(i\) 条边的最大权重。

题解

核心思想：保留 \(O(\operatorname{poly}(k))\) 条边进行匹配。

首先对于每个左部点，只有边权前 \(k\) 大的右部点是有用的，因此可以筛选出 \(nk\) 条边。

对于每个右部点，只有边权前 𝑘 大的左部点是有用的，因此在上一步筛选的 \(nk\) 条边中再筛一遍。

之后考虑每次匹配一条边，会占用两个点，每个点可能有 \(k\) 条出边。因此匹配一条边会废掉两点的其他至多 \(2k\) 条出边，\(k\) 次匹配最多废掉 \(2k^2\) 条出边。因此在之前筛选的基础上保留前 \(2k^2\) 条边进行匹配即可。

匹配方法就是跑最大费用最大流，每次流 \(1\)，重复 \(k\) 次。

提交记录

[AGC031E] Snuke the Phantom Thief *3514

题意

在二维平面上，有 \(n\) 颗珠宝，第 \(i\) 颗珠宝在 \((x_i,y_i)\) 的位置，价值为 \(v_i\)。

现在有一个盗贼想要偷这些珠宝。

现在给出 \(m\) 个限制约束偷的珠宝，约束有以下四种：

  • 横坐标小于等于 \(a_i\) 的珠宝最多偷 \(b_i\) 颗。
  • 横坐标大于等于 \(a_i\) 的珠宝最多偷 \(b_i\) 颗。
  • 纵坐标小于等于 \(a_i\) 的珠宝最多偷 \(b_i\) 颗。
  • 纵坐标大于等于 \(a_i\) 的珠宝最多偷 \(b_i\) 颗。

现在问你在满足这些约束的条件下，盗贼偷的珠宝的最大价值和是多少。

题解

通过数据范围看出这是一道网络流题目。把一个点拆成表示横纵坐标的两点，发现原问题类似于带限制的二分图最大权匹配，因此考虑费用流建模。

使用偷的珠宝的总个数 \(k\) 作为最大流，枚举 \(k\)。

把一个点拆成表示横纵坐标的两点，先按横坐标排序，限制【横坐标小于等于 \(a_i\) 的珠宝最多偷 \(b_i\) 颗】可以转化为偷的第 \(b_i+1\) 至 \(k\) 颗横坐标都大于 \(a_i\)，限制【横坐标大于等于 \(a_i\) 的珠宝最多偷 \(b_i\) 颗】可以转化为偷的第 \(1\) 至 \(k-b_i\) 颗横坐标都小于 \(a_i\)。

再按纵坐标排序，限制【纵坐标小于等于 \(a_i\) 的珠宝最多偷 \(b_i\) 颗】可以转化为偷的第 \(b_i+1\) 至 \(k\) 颗纵坐标都大于 \(a_i\)，限制【纵坐标大于等于 \(a_i\) 的珠宝最多偷 \(b_i\) 颗】可以转化为偷的第 \(1\) 至 \(k-b_i\) 颗纵坐标都小于 \(a_i\)（其实这一段和上一段同理）。

这样我们知道了横/纵坐标排名为 \(i\) 的珠宝的横/纵坐标范围，进而知道了横/纵坐标排名为 \(i\) 的珠宝可以是哪些。

因此我们建立两个二分图：

  1. 左部点为横坐标排名，右部点为珠宝拆点后表示横坐标的点。
  2. 左部点为纵坐标排名，右部点为珠宝拆点后表示纵坐标的点。

对于每个二分图内部，左右部点之间的边按上面的规则连流量 \(1\) 费用 \(0\) 的边。

由于两个二分图右部点是同一个珠宝拆点形成，因此两个二分图右部点之间表示相同珠宝的点还需要连接流量 \(1\) 费用 \(v\) 的边（\(v\)​ 是这个珠宝的价值）。

然后第一个二分图左部点全连向 \(S\)，第二个二分图左部点全连向 \(T\)，跑最大费用最大流即可。

为了确保流的方向正确，需要将第二个二分图内部的边反向（即右部点连向左部点）。

提交记录

Gym-102201J Jealous Teachers *????

题意

给定一张二分图，左边有 \((n - 1)\) 个点 \(P_i\)，右边有 \(n\) 个点 \(Q_i\)，按照以下规则连边。其中第三类边会在题目中给出，问最大流能否达到 \(n(n - 1)\)。同时需要给出中间流量的方案。满足 \(n \leq 10^5\), \(m \leq 2 \times 10^5\)。

边的连接规则如下：

  • 从源点 \(S\) 到左边的每个点 \(P_i\) 有一条容量为 \(n\) 的边：\((S, P_i, n)\)。
  • 从右边的每个点 \(Q_i\) 到汇点 \(T\) 有一条容量为 \(n - 1\) 的边：\((Q_i, T, n - 1)\)。
  • 在某些给定的左边点 \(P_i\) 和右边点 \(Q_j\) 之间有一条容量为无穷大的边：\((P_i, Q_j, \infty)\)。

题解

引理1：若有解，则二分图存在大小为 \((n-1)\) 的匹配。

证明：首先 \(S\to P_i\) 的边要全部流满才能有解，若不存在大小为 \((n-1)\) 的匹配，则根据 Hall 定理，左侧存在一个点集 \(A\) ，记其能到达的点集为 \(B\)，满足 \(|A|>|B|\)，则有 \(|A|n>|B|(n-1)\)，\(A\) 流不满，因此无解。

因此我们先找到一个匹配，然后流 \((n-1)(n-1)\) 的流量，最后使用右侧未匹配的一个点进行增广，如果能找到若干条增广路经过左侧所有点，就有解了。

做法证明：有解相当于任意删右边一个点，都有完美匹配。考虑由“删掉i”变换为“删掉j”的过程，相当于找到一条 \(i\to j\) 的增广路，所以任意找一组匹配，如果能从失配点找到增广树，到达所有点，则一定有解。

提交记录

额感觉没有完全理解增广路，Mark 一下回头重写一遍。

（另一个人的做题记录，感觉证明更严谨 qaq）

以下认为老师构成左部点，学生构成右部点，即左部点有 \(n\) 个而右部点只有 \(n-1\) 个。

求完美匹配所以考虑先拆下点用 Hall 定理判定合法性。

即有对于任意左部点集合 \(S\)，有 \((n-1)\lvert S\rvert\leq n\lvert N(S)\rvert\)，变下形即 \(\frac{n-1}{n}\leq\frac{\lvert{N(S)}\rvert}{\lvert S\rvert}\)。

显然当 \(|S|<n\) 时这个东西等价于 \(\lvert S\rvert\leq\lvert N(S)\rvert\)，这说明我们任意删除一个左部点均满足剩下的 \(2(n-1)\) 个点存在完美匹配，显然我把每个左部点删一次跑一个二分图匹配，然后把这 \(n\) 组二分图匹配拼起来就是答案。

直接做的复杂度是 \(O(nm\sqrt n)\) 的，但是考虑这其中任意两组二分图匹配的差异都不算很大，具体来说，先把 \(n\) 点删了跑一次二分图匹配，然后将当前状态改为将 \(i\) 点删了的二分图匹配只需要寻找一条在残量网络上 \(n\to i\) 的路径翻转流量即可。所以只需要在残量网络上找一个以 \(n\) 为根的生成树就行了，时间复杂度瓶颈在于第一遍 dinic，为 \(O(m\sqrt n)\) ，可过。

P2764 最小路径覆盖问题 紫

题意

求 DAG 最小路径覆盖。

题解

拆入点和出点，做二分图最大匹配。先将原图视为 \(n\) 个点，每个匹配相当于合并边的左右端点，使用并查集构造答案。

提交记录

2025.6.14

CF1721F Matching Reduction *2800

题意

给定一个二分图，其中左边有 \(n_1\) 个点，右边有 \(n_2\) 个点，共 \(m\) 条边，编号为 \(1 \sim m\)。你需要在线地进行如下 \(q\) 个操作：

  • 操作 1：删去最少数量的点，使得二分图的最大匹配减少恰好 1，并在删除之后，输出当前最大匹配中所有边的编号之和。
  • 操作 2：输出当前在最大匹配中的所有边的编号。

第二种询问只有 \(O(1)\) 次。

题解

引理 1：每次删去仅一个点就可以让最大匹配减少 \(1\)。

引理 1 证明：显然删掉一个点会使最大匹配最多减少 \(1\)，设二分图最大独立集为 \(I\)，最大匹配边集为 \(M\)，所有点构成的集合为 \(V\)，则根据结论 \(|M|=|V|-|I|\)，每次删去一个不在独立集里的点，\(|V|\) 减少 \(1\)，\(|I|\) 不变，因此\(|M|\) 减少 \(1\)。因此可以每次删去一个不在独立集里的点，让最大匹配减少 \(1\)。

因此我们先求出最大匹配，通过最大匹配构造最大独立集，此时不在最大独立集里的点一定被匹配，每次删掉一个不在最大独立集里的点，并删除其匹配边即可。

二分图最大独立集构造方法：先求最大匹配，然后从左侧未匹配点按增广路 bfs 整张图，最大独立集就是左侧未匹配点 + 右侧未被访问的点。（todo）证明这个构造方法的正确性。

提交记录

QOJ # 7185 Poor Students

题意

共有 \(k\) 门课程和 \(n\) 名学生，每名学生需要选择恰好一门课程并通过该课程的考试。如果学生 \(i\) 选择了考试 \(j\)，则该学生的挫败感为 \(c_{i,j}\)。对于每门考试 \(j\)，选择该考试的学生人数不得超过 \(a_j\)。求学生们可能达到的最小总挫败感。

题解

标准费用流模型，但是数据范围太大了流不动。

考虑费用流选择增广路的流程，\(S\to stu_0\to cls_1\to stu_1\to cls_2\to stu_2\to \cdots \to stu_{u-1}\to cls_u\to T\)。

找到增广路后，将原来的匹配方案改成 \(stu_0\to cls_1,stu_1\to cls_2, \dots ,stu_{u-1}\to cls_u\)。

对于每对课程 \((j,k)\)，如果有一个学生 \(i\) 在进行增广时由 \(j\) 换课为 \(k\)，则产生 \(c_{i,k}-c_{i,j}\) 的贡献。

因此我们每新加入一个学生 \(i\) 时，建立一个课程间的图，课程 \(j\) 和课程 \(k\) 之间用堆维护一个边集，表示目前选 \(j\) 的所有学生（记为 \(t\)）的 \(c_{t,k}-c_{t,j}\) 值，实时维护课程被多少学生选择了，类似匈牙利二分图匹配进行增广，每次增广选择最短路。

每次增广使用 SPFA，复杂度 \(O(nVE+nk^2\log n)=O(nk^3+nk^2\log n)\)。

提交记录

P1361 小M的作物 紫

题意

有两片土地，分别是 A 和 B，有 \(n\) 种作物，每种作物有一个种子。将第 \(i\) 种作物种在 A 上，可以获得 \(x_i\) 的收益。将第 \(i\) 种作物种在 B 上，可以获得 \(y_i\) 的收益。
存在一些作物组合（共 \(Q\) 组），对于第 \(i\) 组组合：

  • 如果该组合中的所有作物都种在 A 上，可以获得额外 \(p_i\) 的收益。
  • 如果该组合中的所有作物都种在 B 上，可以获得额外 \(q_i\) 的收益。

制定一种种植作物的方法，使得总收益最大。

题解

直接最小割建模，每个点向 \(S,T\) 分别连接 \(x_i,y_i\) 的边，还有 \(Q\) 个特殊点点，向 \(S,T\) 分别连接 \(p_i,q_i\) 的边。

对于每个特殊点和 \(S\) 或 \(T\) 的连边，要求如果一个边集里任意一条边被割掉，那么这条边也要割掉。

这里有一个建模技巧叫做“并联”建模：

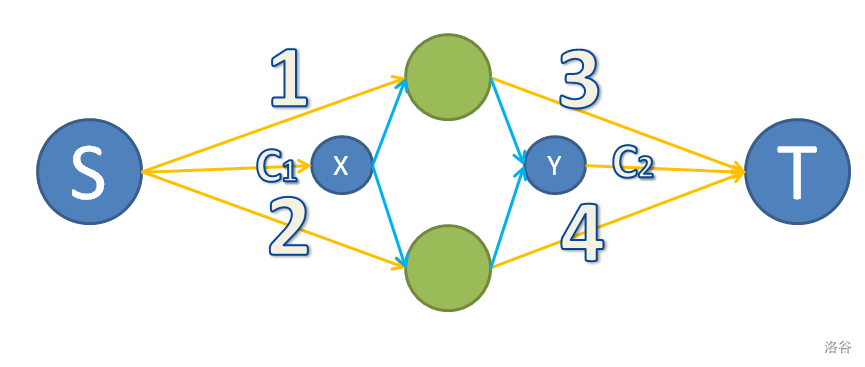
其中蓝色的边权为 \(+\infin\)，不能割。

那么我们发现，如果要使任意一个绿点分离 \(S\)，必须要割掉 \(c_1\) 这条边。

那么直接这样建模就行了。

提交记录

2025.6.15

CF2081 B. Balancing *2500

题意

Ecrade 有一个整数数组 \(a_1, a_2, \ldots, a_n\)。保证对于每个 \(1 \le i < n\)，\(a_i \neq a_{i+1}\)。

Ecrade 可以通过若干次操作将数组变为严格递增的数组。

每次操作中，他可以选择两个整数 \(l\) 和 \(r\)（\(1 \le l \le r \le n\)），并将 \(a_l, a_{l+1}, \ldots, a_r\) 替换为任意 \(r-l+1\) 个整数 \(a'_l, a'_{l+1}, \ldots, a'_r\)。替换后的数组需要满足以下约束：

  • 对于每个 \(l \le i < r\)，\(a'_i\) 和 \(a'_{i+1}\) 之间的比较关系必须与原数组中 \(a_i\) 和 \(a_{i+1}\) 的比较关系相同。即，若原数组中 \(a_i < a_{i+1}\)，则替换后必须有 \(a'_i < a'_{i+1}\)；若原数组中 \(a_i > a_{i+1}\)，则替换后必须有 \(a'_i > a'_{i+1}\)；若原数组中 \(a_i = a_{i+1}\)，则替换后必须有 \(a'_i = a'_{i+1}\)。

题解

找到所有 \(a_i>a_{i+1}\) 的位置，发现每次至多消去两个位置，然后看看第一个位置前面和最后一个位置后面的两个数能不能装下中间的数，分类讨论下即可。

提交记录

CF2081 D. MST in Modulo Graph *2700

题意

给定 \(n\) 个点点权 \(a_1,a_2,\dots ,a_n\)，两个点之间的边权为 \(\max\{a_i,a_j\}\bmod \min\{a_i,a_j\}\)，求这张完全图的 MST。

题解

先去重，然后对于每个二元组 \((a_i,j)\)，\(a\in [j\times a_i,(j+1)\times a_i)\) 的点中只有 \(a\) 最小的点和 \(i\) 连边是有用的，然后边的个数就变成了 \(O(n\ln n)\) 条，跑 kruskal 即可。

提交记录

CF2081C Quaternary Matrix *2600

题意

若矩阵中所有元素均为 \(0\)、\(1\)、\(2\) 或 \(3\)，则称该矩阵为四元矩阵。

当四元矩阵 \(A\) 满足以下两个性质时，Ecrade 称其为好矩阵：

  1. 矩阵 \(A\) 的每一行中所有数字的按位异或（bitwise XOR）结果等于 \(0\)。
  2. 矩阵 \(A\) 的每一列中所有数字的按位异或（bitwise XOR）结果等于 \(0\)。

Ecrade 有一个 \(n \times m\) 的四元矩阵。他想知道将该矩阵变为好矩阵所需修改的最少元素数量，并希望得到其中一个可能的修改后矩阵。

题解

算出每行和每列的异或和，每次操作相当于选一个行和一个列同时异或上一个数字。

先把行和列相同的数字消，此时 行/列 异或和必定只有两种元素，列/行 异或和必定只有一种元素。

然后匹配 行a，行b，列c 之类的情况，发现可以两步消除。

然后匹配 行a，行a，列b，列b 之类的情况，发现可以三步消除。

然后因为行异或和异或上列异或和等于 0，所以我们就做完了。

提交记录

2025.6.16

P2766 最长不下降子序列问题 紫

题意

给定正整数序列 \(x_1 \ldots, x_n\)。

  1. 计算其最长不下降子序列的长度 \(s\)。
  2. 如果每个元素只允许使用一次，计算从给定的序列中最多可取出多少个长度为 \(s\) 的不下降子序列。
  3. 如果允许在取出的序列中多次使用 \(x_1\) 和 \(x_n\)（其他元素仍然只允许使用一次），则从给定序列中最多可取出多少个不同的长度为 \(s\) 的不下降子序列。

\(1 \le n\le 500\)

题解

第一问直接 DP 即可。

第二、三问使用网络流，首先考虑拆点模拟 DP 状态，将一个点拆为 \(O(V)\) 个点，点 \((i,j)\) 表示以 \(i\) 结尾 LIS 为 \(j\) 的状态。然后直接连接所有 \((i,j)\to (i',j+1) (i'>i)\) 的边，跑网络流就是对的。

但是这样一共 \(O(n^2)=(常数)\times 2.5\times 10^5\) 条边，复杂度不能接受。

重新考虑 LIS 的 DP 数组 \(f\)，对于满足 \(j<f_i\) 点 \((i,j)\) 是没用的，因为之后怎么也取不到 LIS，对于满足 \(j>f_i\) 点 \((i,j)\) 也是没用的，因为根本不可能流到这里。

然后只保留点 \((i,f_i)\) 建图即可，点数变成 \(O(n)\)，边数还是 \(O(n^2)\)，dinic 在单位流量稠密图上的复杂度为 \(O(n^{\frac{8}{3}})\)，可以通过。

额数据过水不拆点也能过，但实际是需要拆点保证每个点经过一次的，发了个 工单。

提交记录

P3308 [SDOI2014] LIS 紫

题意

给定序列 \(A\)，序列中的每一项 \(A_i\) 有删除代价 \(B_i\) 和附加属性 \(C_i\)。请删除若干项，使得 \(A\) 的最长上升子序列长度减少至少 \(1\)，且付出的代价之和最小，并输出方案。

如果有多种方案，请输出将删去项的附加属性排序之后，字典序最小的一种。

题解

建图方式和上一题一模一样，只是把不同点之间的连边从 \(1\) 改成了 \(+\infin\)，入点和出点的连边改成了 \(b_i\)，求最小割。

问题就是怎么让最小割的字典序最小。

按 \(c\) 从小到大枚举边，假设枚举到了 \(i\)，把第 \(i\) 条边删掉然后看此时最小割是否恰好减少 \(b_i\)，如果是，就把 \(i\) 加入最小割集合。然后就做完了。

卡常。

判断是不是最小割时不用重跑 dinic，直接看在残量网络上 \(u\) 能不能向 \(v\) 增广即可（即令 \(S=u,T=v\) 然后调用 dinic 的 bfs）。删边时可以使用退流技巧卡常，这样写：

G.maxflow(T,i+n,T,b[i]);
G.maxflow(i,S,T,b[i]);
G.del(i,i+n);

提交记录

（todo）有只跑一遍 dinic 的做法？

P3227 [HNOI2013] 切糕 紫

题意

给你一个长 \(P\)、宽 \(Q\)、高 \(R\) 的长方体点阵。每个点有一个非负的不和谐值 \(v(x,y,z)\)。一个合法的切面满足以下两个条件：

  • 对于每个 \(P\times Q\) 个纵轴，需指定恰一个切割点 \(f(x,y)\)，满足 \(1\le f(x,y)\le R\)。
  • 对于所有的 \(1\le x,x'\le P\) 和 \(1\le y,y'\le Q\)，若 \(|x-x'|+|y-y'|=1\)，则 \(|f(x,y)-f(x',y')| \le D\)，其中 \(D\) 是给定的一个非负整数。

求总的切割点上不和谐值之和的最小值。

题解

看到奇怪的数据范围，考虑最小割模型，边转点，没有第二个限制可以直接做，然后考虑如何刻画第二个限制，发现对于相邻的 \((x,y),(x',y')\)，只需要增加无穷边 \((k-1,x,y)\to (k-1-d,x',y')\) 和 \((k+d,x,y)\to (k,x',y')\) 即可。因为这样可以使 \((k-1,x,y)\to (k,x,y)\) 的边被割掉后必须再割掉一个 \(((k-d)\sim (k+d-1),x',y')\to ((k-d+1)\sim (k+d),x',y')\) 的边才能让 \((k-1,x,y)\) 和 \((k,x,y)\) 真正不连通。

然后跑 dinic 就做完了。

提交记录

额，翻看题解后发现 \((k-1,x,y)\to (k-1-d,x',y')\) 和 \((k+d,x,y)\to (k,x',y')\) 只需添加一种边也是正确的。

P8987 [北大集训 2021] 简单数据结构 黑

题意

实现一个数据结构，维护一个长度为 \(n\) 的序列 \(a\)，支持以下操作 \(q\) 次。

  1. 给定 \(v\)，将所有 \(a_i\) 变为 \(\min(a_i, v)\)。
  2. 将所有 \(a_i\) 变为 \(a_i + i\)。
  3. 给定 \(l, r\)，询问 \(\sum_{i=l}^r a_i\)。

\(1\leq n,q\leq 2\times 10^5\)。

题解

首先如果 \(a\) 初始时都是 \(0\)，那么可以发现 \(a\) 一直是单调的，线段树上二分即可。

这启示我们若 \(a_i=a_j\)，则之后的每一时刻必定满足 \(a_i\leq a_j\)。因此对于一般情况，操作一可以让大于 \(v\) 的数字在之后的操作都变得单调，进一步发现，对于某一次操作时被操作一影响过的位置集合 \(S\)， \(S\) 中的数字也是单调的。证明的话就讨论任意两个元素的大小关系即可。

然后就考虑一个数字在第几次操作二被影响，设第 \(j\) 次操作一前面有 \(cnt_j\) 个操作二，对第 \(i\) 个元素进行二分答案，第 \(i\) 个数在 \([1,mid]\) 被影响，当且仅当 \(\exist j\in [1,mid],a_i+cnt_j\times i\geq v_j\)，变形得 \(\min\limits_{j=1}^{mid} \{v_j-i\times cnt_j\}\leq a_i\)，不等式左侧是一个经典的斜率优化形式，可以通过维护凸包解决，因此对于所有位置，可以整体二分，动态维护凸包求得每个位置加入集合 \(S\) 的时间。也可以分块，每个块维护一个凸包，然后一个块一个块往后跳，找到第一个满足条件的块暴力即可。这里我实现的时候使用了 \(O(\sqrt {n})\) 的分块做法。

然后后面就好做了，对于 \(S\)，维护一颗线段树，支持线段树上二分，区间推平。对于 \([1,n]/S\)，维护一颗树状数组即可。

提交记录

2025.6.17

CF1787G Colorful Tree Again *3000

题意

给定一棵有 \(n\) 个节点的树，边有边权和颜色。每个点有被摧毁和不被摧毁两种状态，初始所有点都没被摧毁。定义一条简单路径是好的，当且仅当路径仅有某一种颜色 \(c\) 构成，且所有颜色为 \(c\) 的边都在这条简单路径里，且路径上所有节点都没被摧毁。

你需要处理两种操作：

  1. 摧毁一个节点；
  2. 修复一个节点。

每个操作之后，你都需要输出最长的好的路径长度。若没有输出 \(0\)。

题解

首先如果颜色 \(c\) 不构成一条链，那么不可能有颜色 \(c\) 的好路径，如果颜色 \(c\) 构成一条链，那么当这条链所有点没有被摧毁时，这条链就是好路径。

那么其实问题相当于给定 \(O(n)\) 条路径，每次摧毁或修复一个点，问最长的完好的路径长度。

发现这题的难点在于改一个点会影响到最多 \(O(n)\) 条路径的状态，进一步发现，修改点 \(i\) 所影响的路径中，至多有一条路径的 \(\operatorname{lca}\neq i\)（即经过这个点和这个点父亲的路径，记为路径 \(L\)），于是考虑将每个路径的 \(\operatorname{lca}\) 处记贡献，每个点存储 \(\operatorname{lca}\) 为这个点的所有路径，这个点的贡献就是这个点存储的所有路径的长度最大值，答案就是所有点贡献的最大值，每次 ban 点的时候直接把这个点贡献去掉，然后在路径 \(L\) 的 \(\operatorname{lca}\) 处删掉 \(L\) 的贡献即可。修复点也是同理的

考虑使用数据结构维护上面的东西。

全局维护一个数据结构，表示每个点的贡献组成的集合，支持：删除、插入、求最大值。

每个点维护一个数据结构，表示以这个点为 \(\operatorname{lca}\) 的路径集合，支持：删除、插入、求最大值。

这些操作可以使用可删堆维护，然后就做完了。

提交记录

CF1464F My Beautiful Madness *3500

题意

给定一颗大小为 \(n (n \leq 2 * 10^5)\) 的树，\(m (m \leq 2 * 10^5)\) 次操作，维护一个初始为空的路径集合 \(P\)。

定义树上一条路径的 \(d\) 邻居（一个点集）\(S\) 为：\(x \in S\) 当前仅当存在一个路径上的点 \(y\) 满足 \(dis(x, y) \leq d\)。

操作分为三种：

  1. 输入 \(u, v\)，在 \(P\) 中加入 \(u\) 到 \(v\) 的路径。
  2. 输入 \(u, v\)，删除 \(P\) 中一个 \(u\) 到 \(v\) 的路径。
    （注意 \(u\) 到 \(v\) 的路径与 \(v\) 到 \(u\) 的路径是相同的，若有多个 \(u\) 到 \(v\) 的路径只删除一个）
  3. 输入 \(d\)，询问 \(P\) 中所有路径的 \(d\) 邻居交集是否为空，若不为空输出 Yes，否则输出 No。

题解

核心思路：对于每个操作 \(3\)，选一个特殊点 \(X\)，满足如果存在交集，则 \(X\) 一定在交集内，然后将问题转化为判定问题。

考虑集合 \(P\) 中 lca 深度最大的路径，取其 lca，记为 \(l\)，记 \(l\) 的 \(d\) 级祖先 \(X\)，可以证明，若存在交集则 \(X\) 一定在交集内，换句话说，如果 \(X\) 不在交集内，则不存在交集。

考虑如何判定 \(X\) 是否在交集内，仿照刚才的思路，取 \(X\) 的 \(d\) 级祖先 \(Y\)，要求所有路径与子树 \(Y\) 有交。

把路径分为类：

  1. lca 在 \(Y\) 子树外
  2. lca 在 \(Y\) 子树内

对于第一类路径，要求其端点必须与子树 \(Y\) 有交。

对于第二类路径，要求其到 \(X\) 的最短距离小于等于 \(d\)。

第一类路径已经能通过 dfn 序+二维数点做了，考虑第二类路径。

考虑一条路径到 \(X\) 的距离在哪个点取最小值：

  1. 与 \(X\to Y\) 的链无交时，这个路径的 lca 处到 \(X\) 的距离取最小值。
  2. 与 \(X\to Y\) 的链有交时，其 lca 处不一定取到最小值，但一定满足 \(\leq d\) 的条件。

因此只计算 \(X\) 到第二类路径 lca 的最大值，然后判断其是否小于 \(d\) 即可。

然后就变成了这样的问题：

  1. 启用一个点
  2. 关闭一个点
  3. 查询一个点到一个子树内所有启用的点的距离最大值。

这个东西直接线段树维护直径就能解决，然后就做完了。

提交记录

The 2nd Universal Cup Finals F. World of Rains *????

题意

有一个 \(N \times M\) 网格，初始所有格子都没有水，每秒发生以下事件：

  1. 降雨：对于每个当前没有水滴的单元格，魔法猫咪独立且随机地决定是否在该单元格中创建一个新的水滴。
  2. 移动（除了在第 \(S+1\) 秒）：所有现有的水滴由于重力和风同时移动。一个位于单元格 \((x, y)\) 的水滴移动到单元格 \((x+1, y+d_i)\)。
  3. 消失：任何移出 \(N \times M\) 网格边界的水滴将永久消失。

任务是计算不同可能的降雨场景的数量。两个场景被认为是不同的，当且仅当在某个单元格 \((i, j)\) 和某个时间 \(t\)（\(1 \leq t \leq S+1\)）中，在一个场景中创建了水滴，而在另一个场景中没有。结果需要对 \(998,244,353\) 取模。

题解

水珠不固定，移动很困难，因此考虑相对的移动整个矩形网格。

图

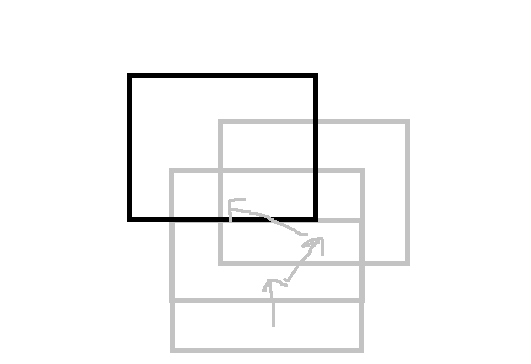
如果一个格点被 \(K\) 个矩形包含，则有 \(K+1\) 种情况：

  • 一直不放水珠。
  • 在第 \(i\ (1\leq i\leq K)\) 时刻放置水珠，之后保持有水的状态。

因此，如果将一个格子被覆盖的时间段拿出来单独算，那么计算方法为：将被覆盖的时间分为若干连续段，则这个格子对答案的贡献为 \(\prod (连续段长度+1)\)，之后将所有点贡献乘起来即可。

现在我们会了多项式复杂度做法，考虑优化。

考虑每一列的贡献，如果这一列被连续覆盖了 \(K\) 秒（相同的列被不连续时段覆盖则视为两列），则被覆盖的每个格子的覆盖次数自上而下形如：

\(1,2,\dots ,\min\{N,K\},\min\{N,K\},\min\{N,K\},\dots ,2,1\)

其中 \(N\) 与题目定义相同，表示矩形的行数。

如果知道 \(K\)，直接预处理阶乘，使用快速幂运算上面所有数的乘积即可。

现在要维护这些列，考虑双端队列维护连续段，每次向左/右平移相当于多出来一个连续段，在从另一端删除若干个离开矩形的连续段，然后再 fix 一个段的区间。维护时可以类比 fhq_treap 维护区间集合。

每个列的连续段在离开时算贡献，每次离开时至多增加一个连续段，复杂度 \(O(\sum S \log {N})\)。

提交记录

2025.6.18

补 2025.6.15 模拟赛，于 2025.6.18 下午进行 vp。

T1

题意

给你一个长度为 \(n\) 的序列，每次操作可以交换相邻两项，问至少几次操作使序列满足：

  • 存在 \(k\)，使序列在 \([1,k]\) 单调不降，在 \([k,n]\) 单调不增。

题解

part 1. 胡扯

先听我瞎扯一段。枚举 \(k\)，然后把 \([1,k]\) 内部变成单调不降，把 \([k,n]\) 内部变成单调不增。记 \(f(z)=\sum\limits_{1\leq x< y\leq z} a_x>a_y,g(z)=\sum\limits_{z\leq x< y\leq n} a_x<a_y\)，则答案为 \(\min\limits_{k=0}^n f(k)+g(k+1)\)。

当然，这是错的。

Hack：

6
10 9 1 6 6 6

正确答案为 2，上述算法得到 3。

part 2. 正解

拆交换贡献，若两个数 \(a,b\) 进行交换，且 \(a<b\)，则在点 \(a\) 处记贡献。

观察序列最终形态，题目要求可等价为：

  • 对于任意 \(i\)，要么 \(i\) 左边都比 \(i\) 小，要么 \(i\) 右边都比 \(i\) 小。

结合我们拆贡献的方法，得出：

  • 如果 \(i\) 左边都比 \(i\) 小，那么这个点在需要与在原序列上左边比他大的数字进行交换。
  • 如果 \(i\) 右边都比 \(i\) 小，那么这个点在需要与在原序列上右边比他大的数字进行交换。
  • 对于上述两条，任意两点之间计算独立。

因此每个点的贡献为 \(\min \{左边比它小的数的个数，右边比它小的数的个数\}\)。

最终答案如下：

\[\sum\limits_{i=1}^{n} \min \{\sum\limits_{j=1}^{i-1} [a_j < a_i],\sum\limits_{j=i+1}^{n} [a_j < a_i]\} \]

可以轻松做到 \(O(n\log n)\)。

这道题启示我们在思路错误的时候及时更换整体思路（相信大多数人的第一想法都是 part 1 中的想法）。

提交记录

T2

题意

有一个数轴，你初始时在点 \(x\)，可以在任意时刻执行以下操作：

  • 假设你现在在点 \(a\)，选择任意的 \(b\)，移动到点 \(b\) 并花费 \(|b-a|\) 元。

同时，有 \(n\) 个区间 \([l,r]\)，你需要按输入顺序执行以下操作：

  • 假设你现在在点 \(a\)，选择一个 \(b\) 满足 \(l\leq b\leq r\)，不进行移动并花费 \(|b-a|\) 元。

求最小花费。

题解

slopetrick 的板子。

先设计一个 \(O(nV)\) 的 DP，\(dp_{i,j}\) 表示时刻 \(i\) 在位置 \(j\) 的最小花费，转移显然。

打表发现 DP 数组可以分为至多三段，一段斜率 \(-1\)，一段斜率 \(0\)，一段斜率 \(1\)。

考虑如何证明这件事情，初始时，DP 数组分为两段，即 \([-\infin,x]\) 斜率为 \(-1\)，\([x,+\infin]\) 斜率为 \(1\)。

加入区间 \([l,r]\) 会让 \([-\infin,l]\) 的斜率加 \(1\)，\([r,\infin]\) 的斜率减 \(1\)。

然后分类讨论，维护斜率为 \(0\) 的段就行了，代码非常短。

#include<bits/stdc++.h>
using namespace std;
#define int long long
const int inf=1e18;
int n,x;
signed main(){
	ios::sync_with_stdio(false);
	cin.tie(0);
	cout.tie(0);
	cin>>n>>x;
	int L=x,R=x,V=0; 
	for(int i=1;i<=n;i++){
		int l,r;
		cin>>l>>r;
		if(l<=L&&R<=r) continue;
		else if(L<=l&&r<=R){
			L=l,R=r;
		}else if(R<=l){
			V+=l-R;
			L=R;
			R=l;
		}else if(l<=R&&R<=r){
			L=l;
		}else if(r<=L){
			V+=L-r;
			R=L;
			L=r;
		}else if(l<=L&&L<=r){
			R=r;
		}
	}
	cout<<V<<"\n";
	return 0;
}

提交记录

T4

刚看 T3 感觉不太能做，于是来看 T4 了。

题意

【CSP-S 2024 T3 染色】的加强版。

给定一个长度为 \(n\) 的正整数数组 \(A\)，其中所有数从左至右排成一排。

你需要将 \(A\) 中的每个数染成红色或蓝色之一，然后按如下方式计算最终得分：

设 \(C\) 为长度为 \(n\) 的整数数组，对于 \(A\) 中的每个数 \(A_i\)（\(1 \leq i \leq n\)）：

  • 如果 \(A_i\) 左侧没有与其同色的数，则令 \(C_i = A_i\)。
  • 否则，记其左侧与其最靠近的同色数为 \(A_j\)，则令 \(C_i = |A_i-A_j|\)。

你的最终得分为 \(C\) 中所有整数的和，即 \(\sum \limits_{i=1}^n C_i\)。你需要最小化最终得分，请求出最终得分的最小值。

题解

看标题，这道题首次出现时间应该是在 2023-9-27，所以这道题的出题人压中了 CSP-S 2024 的第三题？（大雾）

仿照【CSP-S 2024 T3 染色】，记 \(S_i=\sum\limits_{j=2}^{i} |A_j-A_{j-1}|\)，设 \(f_{i,1/0}\) 表示只考虑前 \(i\) 项的最小值，当前颜色与上一个颜色是否相同，讨论转移：

  • \(i\) 与 \(i-1\) 同色，\(f_{i,1}=\min \{f_{i-1,0},f_{i-1,1}\}+|A_i-A_{i-1}|\)。
  • \(i\) 与 \(i-1\) 不同色，\(f_{i,0}=\min\limits_{j=1}^{i-1} \{f_{j,0}+S_{i-1}-S_j+|A_i-A_{j-1}|\}\)。

上述转移原理与【CSP-S 2024 T3 染色】几乎一致。

现在有 \(O(n^2)\) 做法了，考虑优化。

同色转移可以直接 \(O(1)\) 了，不同色转移可以写成如下形式：

\[f_{i,0}\leftarrow f_{j,0}-S_j-A_{j-1}+S_{i-1}+A_i\ (A_{j-1}\leq A_i)\\ f_{i,0}\leftarrow f_{j,0}-S_j+A_{j-1}+S_{i-1}-A_i\ (A_{j-1}>A_i) \]

转移式子可分为和 \(j\) 有关与和 \(i\) 有关的两部分，有一个维度有限制，这是一个经典的数据结构优化 DP 形式，随便优化一下就 \(O(n\log n)\) 了。

提交记录

T3

原题链接

题意

现有一个环，环上有 \(n\) 个数，第 \(i\) 个数是 \(a_i\)，其中第 \(i(1 \leq i < n)\) 个和第 \(i+1\) 个相邻，第 \(n\) 个和第 \(1\) 个相邻。

每次操作你可以做以下事情之一：

  1. 选取 \(i\)，设 \(l, r\) 分别为与 \(i\) 左右相邻的数，将 \(a_i\) 变为 \(\min(a_i, a_l, a_r)\)。
  2. 选取 \(i\)，设 \(l, r\) 分别为与 \(i\) 左右相邻的数，将 \(a_i\) 变为 \(\max(a_i, a_l, a_r)\)。

你需要对于每个 \(k(1 \leq k \leq m)\) 求出：最少操作多少次，才能使得所有数都等于 \(k\)。

题解

一开始错误的思路

对于每个 \(k\)，把环按 \(k\) 拆成若干段计算答案，发现如果当前数的后面两个数中一个大于 \(k\)，另一个小于 \(k\)，那么需要两次操作将后面一个数字改成 \(k\)，否则只需要一次操作。

所以每个段的答案就是段长加上相邻两项关于 \(k\) 的大小关系不同的位置数，然后只需要断环成链，维护一个线段树，从小到大加数，加数时将线段树上的一位由 0 反转为 1，维护相邻不同的位置数即可。

但是真的是这样吗？

Hack：3 2 2 2 2 5 2 2 2 3（\(k=3\)），发现只需要将 \(5\) 花费一步调整为 \(2\)，然后再加上段长即可。

多造几组 Hack，发现难点在于形如 010101 交替的情况，然后我就不会了。

正解

遇到这种情况，直接从难点入手，考虑极长的 01 交替子串，发现最优策略是将 \(0\) 全部调为 \(1\)，或将 \(1\) 全部调为 \(0\)。因此长为 \(len\) 的极长 01 交替子串的贡献为 \(\frac{len}{2}\)。

因此，将上述错误思路的算贡献部分，由“相邻不同的位置数”，改为“极长 01 交替子串的长度整除 \(2\) 之和”即可。

维护的话就用线段树，类似维护区间最大子段和直接做就行了。

提交记录

2025.6.19

QTREE 4 紫

题意

给出一棵边带权的节点数量为 \(n\) 的树，初始树上所有节点都是白色。有两种操作：

  • C x，改变节点 \(x\) 的颜色，即白变黑，黑变白。

  • A，询问树中最远的两个白色节点的距离，这两个白色节点可以重合（此时距离为 \(0\)）。

边权有负数。

题解

点分树。

建出点分树，利用【两点在点分树上的 lca 一定在原树两点路径上】的性质。

考虑普通 DP 求树上直径的过程，是记 \(mx_u\) 表示子树 \(u\) 内到 \(u\) 的最大距离，之后枚举 lca，找两个 \(mx_v\) 拼起来。

因此点分树上每个点维护 \(C_u\) 表示点分树子树 \(u\) 内到 \(fa_u\) 的集合。

\(P_u\) 表示 \(u\) 每个子树 \(C_v\) 最大值的集合，即 \(P_u=\max \{C_v|fa_v=u\}\)。

当 \(u\) 是白点时，还需要在 \(P_u\) 加上 \(0\)。

答案就是 \(\max\limits_{i=1}^n \max(P_u)+\operatorname{secondmax}(P_u)\)。

每个点的 \(C,P\) 各维护一个可删堆，在维护一个全局可删堆表示 \(\max(P_u)+\operatorname{secondmax}(P_u)\) 的集合，修改是简单的。

提交记录

（todo）把 SPOJ 的 QTREE4 卡常卡过。

[NOI2018] 你的名字 黑

题意

给定 \(S\)，多次询问，每次给定 \(T,l,r\)，问字符串 \(T\) 中有多少本质不同字串，满足其不是 \(S_{l\dots r}\) 的子串。

数据范围为 \(10^6\) 级别。

题解

首先先不管 \(S\)，位置不同但是本质相同的子串肯定不能算重，因此考虑【本质不同子串】套路，把 \(S\) 和所有询问串拼到一起建出 SA。

每次询问求出 \(T\) 的本质不同子串，再减去是 \(S\) 子串的部分。

现在要计算是 \(S\) 子串的部分，考虑 SA 中【双指针求 height】的套路，设 \(L_i\) 表示 \(T\) 的位置 \(i\) 的后缀中，是 \(S\) 子串的最长前缀的长度。

则有 \(L_{i+1}\geq L_i-1\)，证明是容易的。

因此只要我们能 \(O(1)\) 或 \(O(\log n)\) 判断 \(T\) 中的一段是否是 \(S\) 的子串，我们就能双指针求 \(L\)，然后就能向求本质不同子串一样容斥做了。

然后考虑对于 \(T\) 的某个位置在拼接后总串的位置 \(x\)，判定【从这个位置开始 \(len\) 个字符是否是 \(S_{l\dots r}\) 的子串】，只需要查询 \([l,r-len+1]\) 中是否有一个位置 \(y\) 满足 \(\operatorname{lcp}(x,y)\geq len\) 即可。

看到 \(\operatorname{lcp}\) 大于某个数字，因为 \(\operatorname{lcp}\) 运算在后缀排序中有单调性，所以考虑在后缀排序上做这个事情。具体地，在后缀排序中二分出一个区间 \([ll,rr]\) 满足 \(\forall i\in [ll,rr],\operatorname{lcp}(x,sa_i)\geq len\)，然后判定 \(\exist i\in [ll,rr],l\leq sa_i\leq r-len+1\) 是否成立。

判定条件是一个经典的 4-side 二位数点问题，可以主席树维护，然后就可以求出 \(L\) 了。

之后仿照【本质不同子串】的套路容斥一下即可。

略微卡常。

提交记录

2025.6.20

上学。

2025.6.21

上学。

2025.6.22

模拟赛。

T1 *1700

题意

给定一个长度为 \(n\) 的数列 \(a\)，每次操作可以选择一个位置 \(i\)，满足 \(2\leq i\leq n-1\land a_{i-1}<a_i\land a_i>a_{i+1}\)，执行 \(a_i\leftarrow \min(a_{i-1},a_{i+1})-1\)，求最多进行多少次操作。

题解

直接用栈模拟，是 \(O(答案)\) 的，然后发现每次新加入一个数会消除一段连续的递增序列，然后随便维护一下就行了，复杂度 \(O(n)\)，代码量约 400b。

提交记录

T2 *2100

题意

给定一个长为 \(n\) 的序列 \(a\)，初始时对于所有 \(1\leq i\leq n\)，有 \(a_i=i\)，你可以以任意顺序执行以下两种操作若干次：

  • 将序列的 \([1,a]\) 翻转。
  • 将序列的 \([n-b+1,n]\) 翻转。

求有多少种可能的局面。

题解

首先拿出操作序列，发现连续进行同一种操作是没有意义的，所以操作一定是 12 交替。

然后计算重复 12 操作多少次后会回到原点。

直接利用环长 lcm 的套路就行了。

提交记录

T3 *2500

题意

给你一个包含 +，*，(，)，_ 的表达式。

将 \(1\sim m\) 随机填入 _，且同一个数只能用一次。

求表达式结果的期望。

题解

由期望的线性性质，无论 \(a,b\) 是否独立，都有 \(E(a+b)=E(a)+E(b)\)。

将第 \(i\) 个下划线视为 \(x_i\)，拆括号，得到若干个 \(x\) 相乘后相加的式子，例如 (_+_)*(_+_) 变为 x1x3+x1x4+x2x3+x2x4。

用上述式子举例，\(E(x_1x_3+x_1x_4+x_2x_3+x_2x_4)=E(x_1x_3)+E(x_1x_4)+E(x_2x_3)+E(x_2x_4)\)。

通过期望的线性性质将原式拆成了若干个独立的部分，我们只关心每个部分内部的 \(x\) 互不相同即可，而 \(E(x_1x_3),E(x_1x_4)\) 没有任何区别，因此 \(E(x_1x_3)=E(x_1x_4)=E(x_2x_3)=E(x_2x_4)\)。

所以我们算出 \(g_i\) 表示从 \(1\sim m\) 选 \(i\) 个的乘积的期望，\(f_i\) 表示拆括号后 \(i\) 个 \(x\) 乘起来的单项式个数，答案就是 \(\sum f_i\times g_i\)。

\(g\) 可以 01 背包求出，\(f\) 可以建立表达式树后树上背包求出。

提交记录

T4 *????

题意

有一个初始为 \(0\) 的整数变量 \(X\) 和一个长度为 \(n\)、初始全 \(0\) 的 01 序列，对序列进行如下操作：

  • 如果序列全 \(1\)

    • 结束操作。

  • 否则

    • 对于每个满足 \(1\leq i\leq n\) 的整数 \(i\)，同时执行 \(a_i=a_i\lor a_{i+1-n\times [i=n]}\lor a_{i-1+n\times [i=1]}\)。
    • 随机选择一个满足 \(1\leq i\leq n\) 的整数 \(i\)，执行 \(a_i\leftarrow 1\)。
    • 执行 \(X\leftarrow X+1\)。

求操作结束后 \(X\) 的期望值。

题解

我不会，等我会了再写。

（todo）会这道题。

2025.6.23~2025.6.25

准备中考+中考。

2025.6.26

P3449 [POI 2006] PAL-Palindromes 紫

题意

有 \(n\) 个回文串，将这些串两两形成 \(n^2\) 个新串，求新串中有多少个回文串。

题解

串 \(a\) 和串 \(b\) 拼接后是回文串，当且仅当 \(a+b=Rev(b)+Rev(a)\)，然后因为 \(a,b\) 本身都是回文串，所以判定条件可转化为 \(a+b=b+a\)，然后考虑字符串哈希，\(a+b=b+a\) 相当于 \(hash(a)\times base^{len_b}+hash(b)=hash(b)\times base_{len_a}+hash(a)\)。

化简得到 \(\frac{hash(a)}{base^{len_a}-1}=\frac{hash(b)}{base^{len_b}-1}\)，然后就可以随便做了。

提交记录

P3435 [POI 2006] OKR-Periods of Words 蓝

题意

求每个前缀的最长周期之和。

题解

根据 border 周期的结论，只需要求每个前缀的最短非空 border 即可。

考虑 KMP 的同时维护 \(f\) 数组，\(f_i\) 表示前缀 \(i\) 的最短非空 border。

则有：

\[f_i= \begin{cases} f_{border_i},& f_{border_i}\neq 0;\\ border_i,& \text{otherwise}. \end{cases} \]

最终答案为 \(\sum\limits_{i=1\land f_i\neq 0}^{n} i-f_i\)。

提交记录

CF17E Palisection *2900

题意

给你一个字符串 \(s\)，求 \(s\) 中有多少对相交的回文子串。

题解

看到回文子串考虑 manacher。

manacher 求出以 \(i\) 结尾的回文串个数 \(f_i\)，以 \(i\) 为开头的回文串 \(g_i\)。

正难则反，统计不相交的回文子串对数，不相交回文子串对数为 \(\sum\limits_{i=2}^n \sum\limits_{j=1}^{i-1} f_{j}\times g_i\)，前缀和一下可以做到 \(O(n)\)。

略微卡空间。

提交记录

2025.6.27

P3546 [POI 2012] PRE-Prefixuffix 紫

题意

给你一个长度为 \(n\) 的串 \(S\)，求最大的 \(L\) 使得 \(S\) 的 \(L\) 前缀和 \(L\) 后缀循环同构。

题解

发现循环同构相当于一个串是 \(AB\)，另一个串是 \(BA\)。

然后相当于把 \(S\) 划分成 \(ABTBA\) 的形式，其中 \(A\) 是 \(S\) 的 border。

因此可以枚举 border \(A\) 的长度，然后求 \(S\) 去掉两边的 \(A\) 后 border \(B\) 的长度，相加更新答案，这样复杂度是 \(O(n^2)\) 的。

所以我们充分发扬人类智慧，只取前 \(100\) 个 border 和后 \(100\) 个 border 进行枚举，然后就 通过 了。

所以我们分析性质，每次要求的是 \(S\) 中间一段的 border，考虑假设 \(S[l:r]\) 的最长 border 是 \(x\)，那么 \(S[l+1:r-1]\) 的最长 border 一定大于 \(x-2\)，因为可以把 \(S[l:r]\) 的 border 掐头去尾，得到 \(S[l+1:r-1]\) 的一个 border。

换句话说，在一个字符串的头尾各加入一个字符，border 至多增加 \(2\)。

所以我们维护区间 border \(x\)，每次在头部和尾部增加一个字符，令 \(x\) 增加 \(2\)，然后不断减少 \(x\) 直到 \(x\) 符合条件，判断是使用字符串哈希。这部分可以类比 SA 中求 height 的步骤。

注意上文中的 border 需要满足长度不超过原串长度的一半。

提交记录

P3805 【模板】manacher 模板

提交记录

P5163 WD 与地图 黑

题意

有 \(n\) 个点，\(m\) 条边的有向图，点有点权，共有三个操作：

1 a b 删除从 \(a\) 连向 \(b\) 的边，保证这条边存在。

2 a b 表示令 \(a\) 的点权增加 \(b\)。

3 a b 求 \(a\) 城市所在 SCC 前 \(b\) 个点的点权之和。如果 SCC 中的点不足 \(b\) 个则输出该 SCC 所有点的点权总和。

题解

倒着做。

如果是双向边则可以线段树合并。

然后整体二分出对于每条边 \((u,v)\)，\(u\) 和 \(v\) 被计入同一个 SCC 的时间 \(t\)，之后将这条边视为在 \(t\) 时刻 \(u,v\) 之间加入双向边，仍然可以线段树合并。

注意整体二分的时候不应该把上述信息当成操作和询问分开处理，因为动态加边的 SCC 本身是非常难维护的，所以应该把边当成操作和询问合一的东西，然后用并查集把已经加入 SCC 的边缩到一个点中，其余边进入右侧二分结构。之后撤销后再进入左侧二分结构。

提交记录

2025.6.28

CF1252D Find String in a Grid *3000

题意

现有一个由大写字母构成的n行m列矩阵。

定义一个 L 型字符串为，从矩阵某个位置开始，先向右走若干步，再向下走若干步，路径上字符依次连接起来组成的字符串。

再给你 \(q\) 个字符串，问对于每个字符串 \(S\)，在矩阵中有多少个 L 型字符串等于 \(S\)。

题解

对于一个 L 型串，我们在他的拐点处计入贡献，同时，每个拐点只保留一个极长的 L 型串。这样只有 \(O(n^2)\) 个有用的 L 型串。那么问题转化为把所有 L 型串拿出来和所有询问串做多模匹配。

看到多模式串匹配考虑 ACAM，把所有 L 型字符串拿出来建 ACAM 空间肯定会炸，因此对询问串建 ACAM。

然后枚举每个 L 型串，加上 L 型串的贡献，再减去不过拐点的贡献。

具体地，假设 L 型串拐点为 \((x,y)\)，则在 ACAM 上以 \(1\) 的贡献跑一遍整个 L 型串，再以 \(-1\) 的贡献跑一遍 \((x,1)\sim (x,y-1)\) 和 \((x+1,y)\sim (n,y)\) 所对应的串即可。

时间复杂度 \(O(n^3+\sum |S|)\)，空间复杂度 \(O(n^2+26\sum |S|)\)。

提交记录

2025.6.29

SP7258 SUBLEX 紫

题意

求一个字符串本质不同排名第 \(k\) 小的子串。

题解

建立 SAM，预处理每个节点开始走能形成多少个本质不同的子串，可以建反图 DP，然后在 SAM 上沿转移边找第 \(k\) 小子串即可。

提交记录

P6727 [COCI 2015/2016 #5] OOP 紫

题意

给定 \(N\) 个单词和 \(Q\) 个模板，一个模板由一个 * 和一些小写字母组成。一个模板覆盖了一个单词当且仅当将 * 替换为某个字符串（可以为空）后，模板和单词能够完全重合。对于每个模板，求出它能够覆盖多少个单词。

题解

将模板串拆成 pre+*+suf 的形式。

一个单词能被一个模板串覆盖，当且仅当 pre 是这个单词的前缀，suf 是这个单词的后缀，且单词长度大于等于 \(|pre|+|suf|\)。

pre 是这个单词的前缀，转化成前缀字典树中这个单词在 pre 的子树内。

suf 是这个单词的后缀，转化成后缀字典树中这个单词在 suf 的子树内。

然后相当于匹配一个串受到了三维的限制：

  • 前缀字典树 dfn
  • 后缀字典树 dfn
  • 长度

三位数点即可，可以使用树状数组套线段树维护。

提交记录

2025.6.30

CF1975H 378QAQ and Core *3500

题意

给你一个字符串，重排字符串使得所有后缀的最大字典序最小，输出重排后的字符串字典序最大的后缀。

题解

考虑样例 bazoka，不难发现只有一个最大字符时，答案就是最大的字符。

那么从最大字符入手，设最大字符是 \(c\)，那么重排后的字符串肯定是 \((cs_1)(cs_2)(cs_3)\dots (cs_k)c\)。

容易证明 \(c\) 一定在头部和尾部。

如果确定了 \(s_1,s_2,\dots,s_k\)，就可以把重排 \((cs_1)(cs_2)(cs_3)\dots (cs_k)\) 看成一个子问题，递归解决后再加上 \(c\)。

注意每个字符串最后都要接上一个比目前大的后缀，所以比较时不是传统的字符串比大小。解决方法是递归的时候维护字符串集合实时有序。

考虑如何确定 \(s_1,s_2,\dots s_k\)。

记最大字符有 \(cnt\) 个，其余字符有 \(num\) 个。

当 \(cnt\geq num+1\) 时，那么有些 \(s\) 可能是空串，显然平均分配最优，我们让每个其余字符带 \(\lfloor \frac{cnt}{num+1} \rfloor\) 个字符，余下的字符单独进入下一层递归。

例如字符串 \(z^{14}abc\)，递归时会把原串分为 \(z^3a,z^3b,z^3c,z,z\) 进入下一层递归，最后结果再加上 \(z^3\)。

当 \(cnt<num+1\) 时，不会有空的 \(s\)。

首先注意到一个最大的后缀肯定是由最大字符 \(c\) 结尾的。那么肯定先前 \(cnt-1\) 个 \(c\) 后面接上 \(cnt-1\) 个最小的其余字符。

之后考虑什么位置可以作为最大后缀。

例如字符串 \(zzzzaabbcc\)，先把结尾 \(z\) 拿出来，然后填完一轮后变为 \(za,za,zb\)，剩余 \(b,c,c\)。

此时，只有 \(zb\) 能作为最大后缀，所以应该把 \(b,c,c\) 全部接到 \(zb\) 后面，变为 \(za,za,zbbcc\)，使 \(zb\) 尽可能晚的接到下一个 \(z\)，这样最终答案就是 \(zaabbz\)。

如果不这么做，比如你将字符串分成了 \(zab,zac,zbc\)，那么就会存在 \(zbcz\) 的后缀，字典序大于 \(zaabbz\)。

因此，从小到大填，每轮将剩余字符仅填充在目前结尾是最大的字符的字符串之后。

贴一个核心代码。

string core(vector<string> S){
	if(S.size()==0) return "";
	int num=S.size();
	string mx=S[num-1];
	while(num&&S[num-1]==mx) num--;
	int cnt=S.size()-num;
	if(cnt==1){
		return mx;
	}
	if(num+1>=cnt){
		vector<string> nxt;
		for(int i=1;i<cnt;i++){
			nxt.push_back(mx);
		}
		int now=0;
		for(int i=0;i<num;){
			for(int j=now;j<cnt-1;j++){
				nxt[j]+=S[i];
				if(j>now&&S[i]>S[i-1]) now=j;
				i++;
				if(i>=num) break;
			}
		}
		return core(nxt)+mx;
	}else{
		int k=cnt/(num+1);
		vector<string> nxt;
		string kmx="";
		for(int i=1;i<=k;i++) kmx+=mx;
		for(int i=1;i<=num;i++){
			string tmp=kmx+S[i-1];
			nxt.push_back(tmp);
		}
		for(int i=1;i<=cnt%(num+1);i++) nxt.push_back(mx);
		//要实时维护集合有序，这里顺序不能错。
		return core(nxt)+kmx;
	}
}

提交记录

qoj7773 重排 *????

题意

定义一个字符串是好串，当且仅当它本身是它的最小表示。

给定一个由小写字母组成的字符串 \(S\)，将 \(S\) 中的字母重排成一个好串，并最大化这个字符串的字典序。输出重排后的字符串。

题解

与 CF1975H 相同，划分为 \((as_1)(as_2)\dots (as_n)\) 向下递归，注意这里 \(a\) 是最小的字符。

提交记录

QOJ #6842. Popcount Words *????

题意

有无穷 01 字符串 \(S\)，第 \(i\) 项为 \(\operatorname{popcnt}(i)\bmod 2\)。

记 \(w(l,r)\) 表示 \(S_lS_{l+1}\dots S_{r}\)。

给你 \(N\) 个区间 \([l_1,r_1],[l_2,r_2],\dots,[l_n,r_n]\) 和 \(Q\) 个询问串 \(s_1,s_2\dots,s_q\)，问每个询问串在 \(w(l_1,r_1)+w(l_2,r_2)+\cdots +w(l_n,r_n)\) 的出现次数。

题解

看到多模匹配，考虑 ACAM，对询问串建立 ACAM，然后只要统计出 \(w(l_1,r_1)+w(l_2,r_2)+\cdots +w(l_n,r_n)\) 在 ACAM 转移时每个点的经过次数即可。

考虑分析无穷序列 \(S\) 的性质，套路的将其拆分为整二进制形式，拆分后具有如下好处：

  1. 状态数有限
  2. 满足倍增性质

具体地，记：

\[W(j,0)=w(0,2^j-1)\\ W(j,1)=w(2^j,2^{j+1}-1) \]

不难证明：

  1. \(w(k2^j,k2^j+2^j-1)=W(j,k\bmod 2)\)
  2. \(W(j,i)=W(j-1,i)+W(j-1,1-i)\)

由 1，可以将 \(w(l_1,r_1)+w(l_2,r_2)+\cdots +w(l_n,r_n)\) 拆分为若干个 \(W(j,i)\) 拼在一起的形式，而 \(W\) 的状态是 \(O(\sum \log {(r-l+1)})\) 的。

由 2，可以倍增算出 ACAM 上从一个点 \(u\) 做一遍 \(W(j,i)\) 后到达的点，记为 \(f_{u,j,i}\)。

之后考虑计算每个点的出现次数，已经有倍增数组 \(f\) 后，这不需要依赖任何性质，直接逆向倍增即可。可以把倍增结构类比成线段树结构，维护倍增结构的标记下传，记 \(g_{u,j,i}\) 表示从 \(u\) 开始，进行 \(W(j,i)\) 转移的次数。

初始时对于每个拆分出来的 \(W(x,y)\)，打上标记，\(g_{u,x,y}=1\)。

倒着下传标记的转移如下：

\[g_{u,j,i}\to g_{u,j-1,i}\\ g_{u,j,i}\to g_{f_{u,j-1,i},j-1,1-i} \]

最后，对于一个节点 \(u\) ，其总出现次数 \(cnt_{u}=\sum\limits_{f_{v,0,0}=u} g_{v,0,0}+\sum\limits_{f_{v,0,1}=u} g_{v,0,1}\)，也可以写成 \(g_{v,0,i}\to cnt_{f_{v,0,i}}\)。

知道每个点出现次数后在 ACAM 上统计一下 fail 树的子树和就行了。

提交记录

P5446 [THUPC 2018] 绿绿和串串

题意

给定一个非空字符串 \(S\)。

定义翻转操作为：将字符串 \(r_0 r_1 \dots r_{n-1}\) 变为 \(r_0 r_1 \dots r_{n-2} r_{n-1} r_{n-2} \dots r_1 r_0\)。

求所有满足以下条件的 \(x\)：

  1. \(x \le |S|\)。
  2. 存在长度为 \(x\) 的字符串 \(R\)，可以通过若干次翻转得到以 \(S\) 为前缀的字符串。

题解

注意到 \(R\) 一定是 \(S\) 的前缀，所以枚举前缀然后暴力检验即可，因为翻转 \(\log\) 次就超过 \(|S|\) 了。

检验一个串是否是回文串，使用 manacher 即可。

提交记录

posted @ 2025-07-02 13:09  george0929  阅读(25)  评论(0)    收藏  举报