虚树
虚树
什么是虚树???!!!
一听这名字就感觉是个玄学东西,第一次听到这个名词还是在任轩笛大佬讲课时听到的。。。当时本来就快在坐飞机了,然后看到这个名词后,我想我应该真的起飞了。。。
然后又是凯爷图论专讲时听了虚树(不要问我为什么在图论里。。。),感觉好像有点头绪,以为第二天会考虚树,然后就恶补,然而还是花了好久才懂了。。。
那么什么是虚树,是个玄学东西吗?
虚树也是一种树吧(虽然网上很多人说这不是树,但我觉得不应该因为叫虚树就歧视别人。。。),对于一棵很大的树,我们直接在上面进行操作时(一般是树形动规)往往复杂度会很爆炸,然而我们会发现询问的点其实很少,这些点我们称之为关键点,发现大部分不查询的点其实都是没有用的,我们只需要根据关键点建立一棵更小的树,然后只用维护关键点的信息,然后在虚树上DP就很妙妙了。
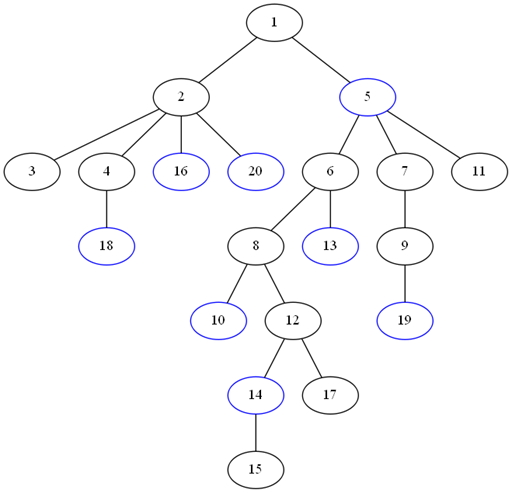
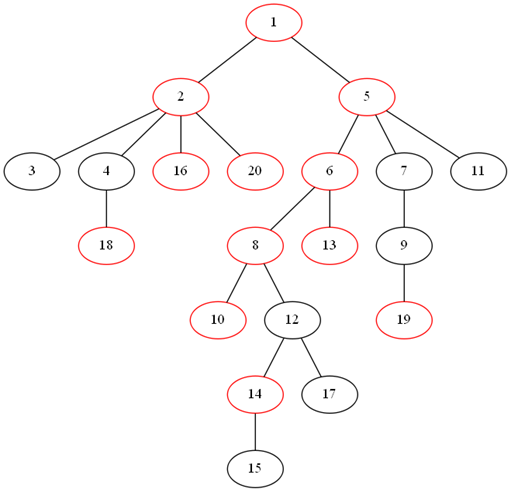
为了和谐,我们来直观地感受一下...比如这里我生成了一棵20个点的树。蓝色的是询问点。红色点就会在虚树上。
观察这些虚树上的点,我们发现我们似乎是需要把询问点按dfs序排序一下,然后把相邻点取个lca然后乱搞一下?
听起来好像很有道理,不过这TM能写?
基于这样的想法,我们来考虑另外一种做法,我们用一个栈来维护虚树的“当前这一坨东西”...例如我们在栈中加入了18。然后接下来打算加入一个16。
我们现在发现这个栈顶的lca,也就是2,是有用的,那么我们现在就要把18弹掉,换成2,然后再扔进去一个16。
接下来我们要加一个20,那么它与栈顶的lca为2。我们就考虑16,16是没用的,把它弹掉,然后看见2,正好就是lca,就保留。
类似这样我们可以发现开始把所有询问点加入虚树后,我们把询问点按dfs序排个序,这时栈里面应该维护一个奇怪的玩意,先计算一个新加的点与栈顶的lca,然后如果一个栈里的东西一直都“没用”,也就是深度比这个lca来得大,就一直弹出栈顶,最后如果栈顶不是lca,就把lca加入栈,并且加入虚树,然后再加入这个点。
这样我们就可以求出虚树啦,同时我们也可以得到虚树上每一个点的父亲节点。
当然上面只是让你对虚树有个大致了解,不过要是你没有大致了解的话,下面可能有点伤。。。(万一你是大佬。。。当我没说)
我们以一道题为例:
题目传送门
首先看到这道题我们会想到每次O(n)去DP,发现对于一个非关键点我们有两种选择,一个是将其与祖先节点的路径上的最短边断了,或者将子树中的所有关键点断了,对于关键点,显然你只能将其祖先节点的路径上的最短边断了。总的复杂度O(n*q),然后我们考虑用虚树去优化。
我们需要维护的就是每个节点到根节点的路径上的最短边,然后建立虚树,这个信息在虚树上仍可以使用。
怎么构建虚树
维护一个栈,表示从根到栈顶元素的这条链
我们新加入一个节点记为x,链的末端,即栈顶,为p,lca为lca(x,p),
有两种情况:
1.p和x分立在lca的两棵子树下.
2.lca是p.
为什么lca不能是x?
因为如果lca是x,说明dfn[lca]=dfn[x]<dfn[p],而我们是按照dfs序号遍历的,于是dfn[p]<dfn[x],矛盾.)
对于第二种情况,直接在栈中插入节点x即可,不要连接任何边(会在之后构建时才连边).
对于第一种情况,要仔细分析.
我们是按照dfn遍历的(因为很重要所以多说几遍......),有dfn[x]>dfn[p]>dfn[lca].
这说明什么呢? 说明一件很重要的事:我们已经把lca所引领的子树中,p所在的子树全部遍历完了!
简略的证明:如果没有遍历完,那么肯定有一个未加入的点h,满足dfn[h]<< dfn[x],
我们按照dfs序号递增顺序遍历的话,应该把h加进来了才能考虑x.
这样,我们就直接构建lca引领的,p所在的那个子树. 我们在退栈的时候构建子树.
p所在的子树如果还有其它部分,它一定在之前就构建好了(所有退栈的点都已经被正确地连入树中了),就剩那条链.
如何正确地把p到lca那部分连进去呢?
设栈顶的节点为p,栈顶第二个节点为q.
重复以下操作:
如果dfn[q]>dfn[lca],可以直接连边q->p,然后退一次栈.
如果dfn[q]=dfn[lca],说明q=lca,直接连边lca->p,将x弹出,此时子树已经构建完毕.
如果dfn[q]< dfn[lca],说明lca被p与q夹在中间,此时连边lca->p,退一次栈,再把lca压入栈.此时子树构建完毕
最后,为了维护dfs链,要把x压入栈. 整个过程就是这样,然后我们就可以树上DP了。
最后再放上一张动图,然你更好地理解虚树:
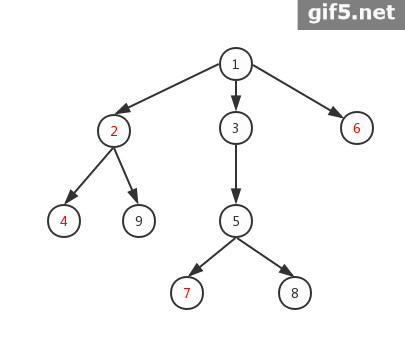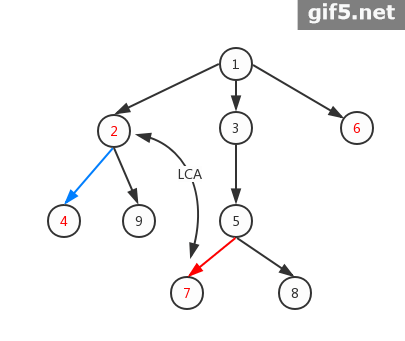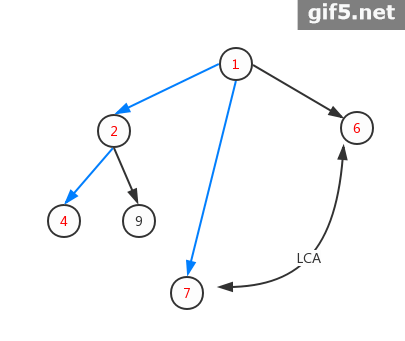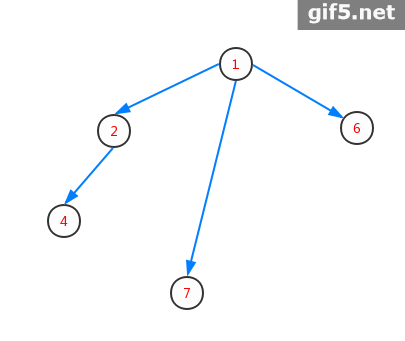
这里再提一下每次重构虚树的小优化我们只需要在DP时,在访问完一个节点的所有出边后,把head数组清零即可
【代码实现】
1 #include<cstdio> 2 #include<cstring> 3 #include<algorithm> 4 #include<cctype> 5 #include<queue> 6 using namespace std; 7 void read(int &v) 8 { 9 int f;char ch; 10 while(!isdigit(ch=getchar())&&ch!='-'); ch=='-'?(f=-1,v=0):(f=1,v=ch-'0'); 11 while(isdigit(ch=getchar())) v=v*10+ch-'0';v=v*f; 12 } 13 const int N=250005; 14 const long long INF=1e12+7; 15 struct sd{ 16 int next,to,w; 17 }edge[2][N<<1]; 18 int head[2][N],dep[N],dfn[N],stk[N],pos[N],up[N][21],n,m,cnt; 19 long long dp[N],exp[N]; 20 bool cmp(int a,int b) {return dfn[a]<dfn[b];} 21 void add_edge(int from,int to,int w,int opt) 22 { 23 if(from==to) return; 24 edge[opt][++cnt].next=head[opt][from]; 25 edge[opt][cnt].to=to; 26 edge[opt][cnt].w=w; 27 head[opt][from]=cnt; 28 } 29 void pre_work(int v,int ff) 30 { 31 dfn[v]=++cnt,up[v][0]=ff,dep[v]=dep[ff]+1; 32 for(int i=1;i<=20;i++) up[v][i]=up[up[v][i-1]][i-1]; 33 for(int i=head[0][v];i;i=edge[0][i].next) 34 { 35 int to=edge[0][i].to; 36 if(to!=ff) 37 exp[to]=min(exp[v],(long long)edge[0][i].w),pre_work(to,v); 38 } 39 } 40 int LCA(int a,int b) 41 { 42 if(dep[a]<dep[b]) swap(a,b); 43 int len=dep[a]-dep[b]; 44 for(int i=20;i>=0;i--) if(len&(1<<i)) a=up[a][i]; 45 if(a==b) return a; 46 for(int i=20;i>=0;i--) if(up[a][i]!=up[b][i]) a=up[a][i],b=up[b][i]; 47 return up[a][0]; 48 } 49 void build(int mx) 50 { 51 cnt=0; 52 int top=0; 53 sort(pos+1,pos+1+mx,cmp); 54 int tot=0; 55 pos[++tot]=pos[1]; 56 for(int i=2;i<=mx;i++) 57 if(LCA(pos[tot],pos[i])!=pos[tot]) pos[++tot]=pos[i]; 58 stk[++top]=1; 59 for(int i=1;i<=tot;i++) 60 { 61 int now=pos[i],lca=LCA(now,stk[top]); 62 while(1) 63 { 64 if(dep[lca]>=dep[stk[top-1]]) 65 { 66 add_edge(lca,stk[top--],0,1); 67 if(stk[top]!=lca) stk[++top]=lca; 68 break; 69 } 70 add_edge(stk[top-1],stk[top],0,1),top--; 71 } 72 if(stk[top]!=now)stk[++top]=now; 73 } 74 while(--top) add_edge(stk[top],stk[top+1],0,1); 75 } 76 void DP(int v) 77 { 78 long long tmp=0;dp[v]=exp[v]; 79 for(int i=head[1][v];i;i=edge[1][i].next) 80 { 81 int to=edge[1][i].to; 82 DP(to); 83 tmp+=dp[to]; 84 } 85 head[1][v]=0; 86 if(tmp) dp[v]=min(dp[v],tmp); 87 } 88 int main() 89 { 90 int a,b,c,k; 91 read(n); 92 for(int i=1;i<n;i++) 93 read(a),read(b),read(c),add_edge(a,b,c,0),add_edge(b,a,c,0); 94 cnt=0,exp[1]=INF,pre_work(1,0); 95 read(m); 96 for(int i=1;i<=m;i++) 97 { 98 read(k); 99 for(int j=1;j<=k;j++) 100 read(pos[j]); 101 build(k); 102 DP(1); 103 printf("%lld\n",dp[1]); 104 } 105 return 0; 106 }


 浙公网安备 33010602011771号
浙公网安备 33010602011771号