[bzoj1568][JSOI2008]Blue Mary开公司——李超线段树

题目大意

题解

这道题需要用到一种叫做李超线段树的东西。我对于李超线段树，是这样理解的：
给节点打下的标记不进行下传，而是仅仅在需要的时候进行下传，这就是所谓永久化标记。
对于这道题，借用一张图，

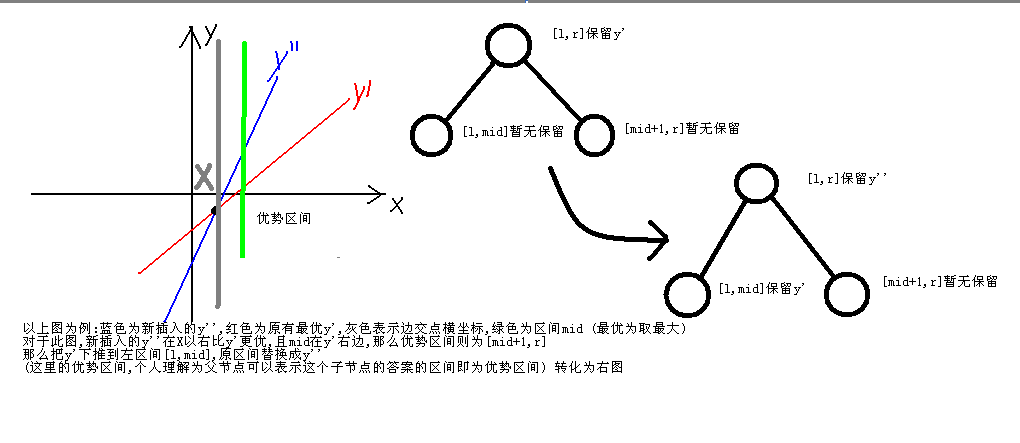
这张图解释的比较清楚了。

代码

#include <algorithm>
#include <cctype>
#include <cstdio>
int read() {
  int x = 0, f = 1;
  char ch = getchar();
  while (!isdigit(ch)) {
    if (ch == '-')
      f = -1;
    ch = getchar();
  }
  while (isdigit(ch)) {
    x = x * 10 + ch - '0';
    ch = getchar();
  }
  return x * f;
}
int N, M;
struct line {
  double k, b;
  int id;
  double getf(int x) { return k * x + b; };
};
bool cmp(line a, line b, int x) {
  if (!a.id)
    return 1;
  return a.getf(x) != b.getf(x) ? a.getf(x) < b.getf(x) : a.id < b.id;
}
const int maxn = 50010;
line t[maxn << 2];
line query(int k, int l, int r, int x) {
  if (l == r)
    return t[k];
  int mid = (l + r) >> 1;
  line tmp;
  if (x <= mid)
    tmp = query(k << 1, l, mid, x);
  else
    tmp = query(k << 1 | 1, mid + 1, r, x);
  return cmp(t[k], tmp, x) ? tmp : t[k];
}
void insert(int k, int l, int r, line x) {
  if (!t[k].id)
    t[k] = x;
  if (cmp(t[k], x, l))
    std::swap(t[k], x);
  if (l == r || t[k].k == x.k)
    return;
  int mid = (l + r) >> 1;
  double X = (t[k].b - x.b) / (x.k - t[k].k);
  if (X < l || X > r)
    return;
  if (X <= mid)
    insert(k << 1, l, mid, t[k]), t[k] = x;
  else
    insert(k << 1 | 1, mid + 1, r, x);
}
void Insert(int k, int l, int r, int x, int y, line v) {
  if (x <= l && r <= y) {
    insert(k, l, r, v);
    return;
  }
  int mid = (l + r) >> 1;
  if (x <= mid)
    Insert(k << 1, l, mid, x, y, v);
  if (y > mid)
    Insert(k << 1 | 1, mid + 1, r, x, y, v);
}
int main() {
#ifdef D
  freopen("input", "r", stdin);
#endif
  M = read();
  N = 50000;
  char opt[15];
  while (M--) {
    scanf("%s", opt);
    if (opt[0] == 'P') {
      double k, b;
      scanf("%lf %lf", &k, &b);
      line tmp;
      tmp.k = b;
      tmp.b = k - b;
      tmp.id = 1;
      Insert(1, 1, N, 1, N, tmp);
    }
    int x;
    if (opt[0] == 'Q') {
      x = read();
      printf("%lld\n", (long long)(query(1, 1, N, x).getf(x) / 100 + 1e-8));
    }
  }
  return 0;
}