端到端的机器学习项目

加州住房价格分析实例

1. 写在前面

本文介绍一个端到端的项目案例，基于加州住房价格数据集，建立起加州的房价模型。本文将详细重现建模过程，在形成分析框架的基础上为以后的数据分析项目积累实际项目经验。

本文将分为以下部分：

总体框架
获取数据
EDA
数据准备
选择和训练模型
模型调参

本文使用数据集来源于Hands-On Machine Learning with Scikit-Learn, Keras & TensorFlow

代码环境：jupyter labAnaconda环境搭建

开搞！

2. 分析框架

在一个完整的业务流程下，项目模型的输出结果（对一个区域房价中位数的预测）将会跟其他许多信号被传输到另一个机器学习系统，进而被用来决策是否值得投资。下图是一个针对房地产投资的机器学习流水线（一个序列的数据处理组件）。

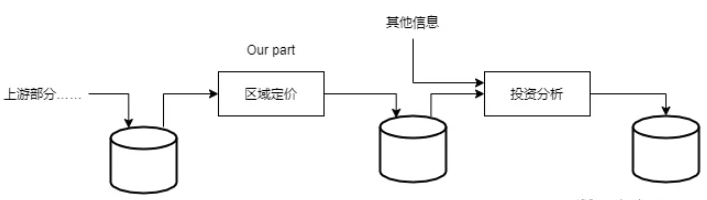
2.1 框架问题

首先需要回答这是有监督学习、无监督学习还是强化学习？是分类任务、回归任务还是其他任务？应该使用批量学习还是在线学习技术？我们针对这些问题一一回答，确定我们的模型框架。

显然，这是一个有监督学习任务。因为已经给出了标记的训练实例（每个实例都有预期的产出，也就是该区域的房价中位数）。同时，这也是个典型的回归任务，因为要对某基于多个特征（区域人口，收入中位数等）对某个值（房价中位数）进行预测。最后，因为并没有连续的数据流，所以不需要针对变化的数据做出特别调整，同时数据量并不算大，所以批量学习足以胜任。

2.2 选择性能指标

在确定分析框架之后，需要选择性能指标，对于回归问题，典型性能指标是均方根误差（RMSE）以及平均绝对误差（MAE）。

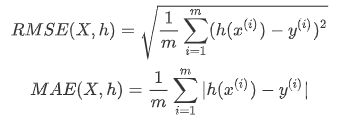
一般情况下，选择RMSE为回归任务的首选性能指标。但是，对于有许多异常区域存在时，可以考虑使用MAE。本文选择RMSE。

3. 获取数据

为了使项目更加自动化，编写了一系列函数来实现数据集的下载、加载，初步查看数据，了解各个特征，最后划分出测试集。

3.1 下载数据

将下载的housing.tgz保存到train/datasets/housing文件夹下，并对数据解压

import pandas as pd
import tarfile
import os
import urllib

DOWNLOAD_ROOT = "https://raw.githubusercontent.com/ageron/handson-ml2/master/"
HOUSING_PATH = os.path.join("train/datasets", "housing")
HOUSING_URL = DOWNLOAD_ROOT + "datasets/housing/housing.tgz"

def fetch_housing_data(housing_url=HOUSING_URL, housing_path=HOUSING_PATH):
    # 如果不存在，则新建文件夹
    if not os.path.isdir(housing_path):
        os.makedirs(housing_path)
    # 保存下载的tgz文件
    tgz_path = os.path.join(housing_path, "housing.tgz")
    # 下载tgz文件并保存至对应路径
    urllib.request.urlretrieve(housing_url, tgz_path)
    # 解压
    housing_tgz = tarfile.open(tgz_path)
    housing_tgz.extractall(path=housing_path)
    housing_tgz.close()

3.2 加载数据

3.2.1 查看数据

使用Pandas快速查看数据结构

def load_housing_data(housing_path=HOUSING_PATH):
    csv_path = os.path.join(housing_path, "housing.csv")
    return pd.read_csv(csv_path)

data = load_housing_data()

使用data.info()快速获取数据集的简单描述。

总共有20640条数据，其中total_bedrooms有207个空值，需要考虑如何这个特征的缺失值。

从数据类型来看，除了ocean_prximity外，其他数据均为数字。这是分类数据，使用value_counts方法查看数据种类。使用describe方法可以获得简单的描述性统计。

另一种快速了解所有数据类型的方法是绘制每个数值属性的直方图。

从直方图来看：

首先，是收入中位数的度量衡，需要清楚收入中位数的计量单位
房龄和房价中位数是有上限的。要注意房价中位数是我们的标签，如果该值可以超出上限，那应该：①对那些标签值被设置上限的区域，重新采样；②或者删除这些标签值超过上限的区域
各个特征的缩放程度并不相同
数据出现厚尾的分布特性。由于某些机器学习算法性能受数据分布的影响，考虑将特征转化为偏正态分布

3.2.2 创建测试集

使用随机抽样

使用sklearn中model_selection模块中的train_test_split对数据集进行纯随机抽样，抽样比例为20%

from sklearn.model_selection import train_test_split

rain_set, test_set = train_test_split(data, test_size=0.2, random_state=42)

使用分层抽样

假设一种情况：收入中位数是一个非常重要的属性，要创建一个收入类别的属性。首先绘制收入直方图

可以看到大多苏收入中位数聚集在1.5~6（万美元）左右，但也有一部分远超6万美元。尝试将收入中位数分成5层：0-1.5、1.5-3、3-4.5、4.5-6、>6。从下图中表格数据可以看到，分层抽样与整体数据集分布几乎一致，而随机抽样是有偏的。

4. EDA

EDA（Exploratory Data Analysis）又名探索性数据分析，在这个阶段，主要通过可视化以及相关性分析对数据集进一步分析。

4.1 可视化

从数据来看，由于存在地理位置信息（经度和维度），因此可以建立一个各区域分布图从而进行可视化。

从最右侧图片来看，价格与地理位置和人口密度息息相关。

4.2 相关性分析

由于数据量并不大，因此可以直接使用corr()方法计算出每对特征之间的标准相关系数（皮尔逊相关系数）。

下图为房价中位数与各特征之间的相关系数：

相关系数的范围从-1变化到1，越靠近1，正相关性越强；越靠近1，则负相关性越强；越靠近0，则说明二者之间没有线性相关性。可以看出房价中位数与收入呈现出很强的正相关性，而与经纬度、人口呈现出负相关。

另一种检测特征之间相关性的办法是使用Pandas中的scatter_matrix函数（根据两两特征之间的相关性总共能得到\(11^2=121\)幅图像，可以根据上文中的相关系数筛选几个重要的特征，每个变量对自身的图像，在这个函数中为直方图）

我们可以看到最有潜力能够预测房价中位数的特征是收入中位数，我们再具体绘制二者的散点图。从下图可以看出，两者之间存在较强的正相关关系。次外，根据之前的分析，50万美元的价格上限是一条清晰的水平线，除此之外，35、45万美元等价格点处也有水平线的痕迹，在下一步的数据准备中可能需要删除这部分数据。

当然我们也可以重新组合各属性。比如获取每个家庭的房间数量等等。

5. 数据准备

接下来，需要为之后的算法准备数据。数据准备主要有以下几项工作：

数据清洗：主要是对缺失值的处理
处理文本和分类属性：One-Hot编码
特征缩放：标准化和归一化

5.1 数据清洗

在查看数据时，发现total_bedrooms有空值，我们可以采取以下三种方法处理空值：

删除对应的数据
删除这个特征
用某个值（0，均值，中位数）填充

# 对应三种方法的代码
housing.dropna(subset=['total_bedrooms'])					# 方法1
housing.drop('total_bedrooms', axis=1)						# 方法2
housing['total_bedrooms'].fillna(median, inplace=False)		# 方法3

sklearn中提供了SimpleImputer来处理缺失值。

5.2 处理文本和分类属性

在处理完数据特征后，还需要处理数据集中的文本属性：ocean_proximity

我们可以使用sklean中的OrdinalEncoder将文本转换成数字（数字的范围是0~分类属性种类-1）。由于此种方法会导致相关性，因此更常规的办法是转换成独热向量。

5.3 特征缩放

标准化：首先减去均值，再除以标准差

归一化：减去最小值，再除以极差

5.4 自定义转换器

可以通过调用sklear中的BaseEstimator，TransformerMixin来实现添加组合属性

# 自定义转换器——添加组合后的属性
from sklearn.base import BaseEstimator, TransformerMixin
rooms_ix, bedroom_ix, population_ix, households_ix = 3, 4, 5, 6

class CombineAttributesAdder(BaseEstimator, TransformerMixin):
    def __init__(self, add_bedrooms_per_room=False):
        self.add_bedrooms_per_room = add_bedrooms_per_room
    def fit(self, X, y=None):
        return self
    def transform(self, X):
        rooms_per_household = X[:, rooms_ix] / X[:, households_ix]
        population_per_household = X[:, population_ix] / X[:, rooms_ix]
        if self.add_bedrooms_per_room:
            bedrooms_per_room = X[:, bedroom_ix] / X[:, rooms_ix]
            return np.c_[X, rooms_per_household, population_per_household, bedrooms_per_room]
        else:
            return np.c_[X, rooms_per_household, population_per_household]

5.5 转换流水线

在数据准备过程中，许多数据转换的步骤需要以正确的顺序来执行。sklearn中的Pipeline方法可以支持这样的转换。

from sklearn.pipeline import Pipeline

num_pipeline = Pipeline([
    ('imputer', SimpleImputer(strategy="median")),
    ('attribs_adders', CombineAttributesAdder()),
    ('std_scaler', StandardScaler())
])

housing_num_tr = num_pipeline.fit_transform(housing_num)

当调用pipeline的fit()方法时，会在所有转换器上按照顺序依次调用fit_transform()，将一个调用的输出作为参数传递给下一个调用方法，最终的估算只会调用fit()方法。

在前面的过程中，分别处理了类别列和数值列，接下来使用sklearn中的ColumnTransformer所有列转换。

from sklearn.compose import COlumnTransformer

num_attribs = list(housing_num)   # 数值列名称列表
cat_attribs = ['ocean_proximity']	# 类别列列表
# 传入一个元组列表，元组包括一个名字，一个转换器（可以是流水线），一个该转换器能应用的列名字（或索引）的列表
full_pipelines = ColumnTransformer([
	('num', num_pipeline, num_attribs),
	('cat', OneHotEncoder(), cat_attribs)
])

housing_prepared = full_pipelines.fit_transform(housing)

需要注意：

转换器必须返回相同数量的行
OneHotEncoder()返回一个稀疏矩阵，而num_pipeline则返回一个密集矩阵，当两者混合时，ColumnTransformer会估算最终矩阵的密度（单元格非零比率），如果低于阈值（默认sparse_threshold=0.3）则会返回稀疏矩阵

6. 选择和训练模型

在做好数据准备之后，是时候开始选择机器学习模型并展开训练了。

6.1 小试牛刀

我们首先使用线性模型进行训练，然后使用sklearn中的mean_squared_error()来测量整个训练集上的RMSE。

from sklearn.linear_model import LinearRegression
from sklearn.metrics import mean_squared_error

lin_reg = LinearRegression()
lin_reg.fit(housing_prepared, housing_labels)			# 训练模型
housing_predictions = lin_reg.predict(housing_prepared)		# 使用训练集预测
lin_mse = mean_squared_error(housing_lables, housing_predictions)	# 计算MSE
lin_rmse = np.sqrt(lin_mse)										# 计算RMSE

预测误差达到68634美元，这是很典型的欠拟合的案例。我们使用更加复杂一点的决策树模型来进行预测。

from sklearn.tree import DecisionTreeRegressor

tree_reg = DecisionTreeRegressor()
tree_reg.fit(housing_prepared, housing_labels)			# 训练模型
housing_predictions = tree_reg.predict(housing_prepared)		# 使用训练集预测
tree_mse = mean_squared_error(housing_lables, housing_predictions)	# 计算MSE
tree_rmse = np.sqrt(tree_mse)										# 计算RMSE

哦！模型的预测误差为0，我们得需要考虑过拟合的问题，因为我们使用训练集进行评估了。我们使用验证集进行模型验证。

6.2 更合理的验证集

要划分验证集可以使用以下两个办法：

使用sklearn中的train_test_split将训练集分为训练集和验证集
使用sklearn中的cross_val_score进行k折交叉验证，产生的结果是包含k评估分数的数组

需要注意：Scikit-Learn中的交叉验证功能将误差当成一种损失（计算出的结果是-MSE）

from sklearn.model_selection import cross_val_score

scores = cross_val_score(tree_reg, housing_prepared, housing_labels,
                         scoring='neg_mean_squared_error', cv=10)
tree_rmse_scores = np.sqrt(-scores)

使用交叉验证得出的误差为69118，可见确实是产生过拟合了。我们再试试两个模型，随机森林和SVM（代码逻辑类似，不再赘述）。

7. 调参

在选择好合适的模型之后，还需要对模型的超参数进行选择。我们可以使用sklearn中的GridSearchCV来对随机森林模型进行调参。

7.1 网格搜索

from sklearn.model_selection import GridSearchCV

param_grid = [
    {'n_estimators': [3, 10, 30], 'max_features': [2, 4, 6, 8]},
    {'bootstrap': [False], 'n_estimators':['3, 10'], 'max_features': [2, 3, 4]},
]
forest_reg = RandomForestRegressor(random_state=42)
grid_search = GridSearchCV(forest_reg, param_grid, cv=5,
                           scoring='neg_mean_squared_error',
                           return_train_score=True)
grid_search.fit(housing_prepared, housing_labels)

# 查看最佳参数
best_params = grid_search.best_params_
# 得到最好的模型组合
best_estimators = grid_search.best_estimators_
# 查看评估分数
cvres = grid_search.cv_results_
for mean_score, params in zip(cvres["mean_test_score"], cvres["params"]):
    print(np.sqrt(-mean_score), params)

得到的最优模型超参数是：max_features=8, n_estimators=30

有些数据准备的步骤也可以作为超参数，使用网格搜索来查找是否添加不确定的特征（比如，是否使用转换器CombinedAttributeAdder的超参数add_bedrooms_per_room）以及寻找处理问题的最佳方法（比如，处理异常值，缺失特征以及特征选择）

7.2 随机搜索

网格搜索适用于搜索组合较少的情况，针对较大搜索范围的超参数调参任务，通常会优先选择RandomizedSearchCV，在每次迭代中为每个超参数选择一个随机值，然后对一定数量的随机组合进行评估。

from sklearn.model_selection import RandomizedSearchCV
from scipy.stats import randint

param_distribs = {
        'n_estimators': randint(low=1, high=200),
        'max_features': randint(low=1, high=8),
    }

forest_reg = RandomForestRegressor(random_state=42)
rnd_search = RandomizedSearchCV(forest_reg, param_distributions=param_distribs,
                                n_iter=10, cv=5, scoring='neg_mean_squared_error', random_state=42)
rnd_search.fit(housing_prepared, housing_labels)

7.3 分析最佳模型及其误差

可以获取每个特征的相对重要程度，并按此排序

feature_importances = grid_search.best_estimator_.feature_importances_

# 每个特征按照重要性排序
extra_attribs = ['rooms_per_houseold', 'population_per_household', 'bedrooms_per_room']
cat_encoder = full_pipelines.named_transformers_["cat"]
cat_one_hot_attribs = list(cat_encoder.categories_[0])
attributes = num_attribs + extra_attribs + cat_one_hot_attribs
sorted(zip(feature_importances, attributes), reverse=True)

7.4 使用测试集评估

在经过训练之后，可以考虑使用测试集评估最终模型。从测试集中获取预测其和标签，运行full_pipelines来转换数据（调用**transform()），然后在测试集上评估最终模型。

final_model = grid_search.best_estimator_

X_test = strat_test_set.drop("median_house_value", axis=1)
y_test = strat_test_set["median_house_value"].copy()

X_test_prepared = full_pipelines.transform(X_test)
final_predictions = final_model.predict(X_test_prepared)

final_mse = mean_squared_error(y_test, final_predictions)
final_rmse = np.sqrt(final_mse)

7.5 保存模型

使用joblib模块保存模型

full_pipeline_with_predictor = Pipeline([
        ("preparation", full_pipelines),
        ("linear", LinearRegression())
    ])

full_pipeline_with_predictor.fit(housing, housing_labels)
my_model = full_pipeline_with_predictor

import joblib
joblib.dump(my_model, "my_model.pkl") # DIFF
#...
my_model_loaded = joblib.load("my_model.pkl") # DIFF

8. 总结

本文基于一个房价分析案例，简要描述了数据获取-分析-建模-调参的全流程，希望能为之后的进一步学习提供完整的分析框架。

posted @ 2021-03-25 20:46 Geek-Thomas 阅读(172) 评论(0) 收藏举报

刷新页面返回顶部

Geek-Thomas