算法分析与设计复习__dp动态规划
-
动态规划
考点(后两列无需考虑)
![]()
1.1基本思想:
动态规划法与分治法类似,也是将原问题分解成若干个子问题,先求解子问题再从这些子问题的解得到原问题的解。与分治法不同的是,子问题往往不是相互独立的。动态规划法所针对的问题有一个显著的特征,即它所对应的子问题树中的子问题大量重复出现。
因此动态规划法的相应特征是,对于重复出现的子问题,只在第一次遇到时进行求解,并把答案保存起来,以后再遇到相同子问题时直接引用,不必重新求解。
1.2设计步骤:
动态规划算法的设计有4个步骤
(1)刻画最优解的结构。
(2)递归定义最优解的值。
(3)以自底向上的方式计算最优解的值。
(4)根据计算最优值时得到的信息构造问题最优解.步骤(1)-(3)是动态规划的基本步骤。对于给定问题,如果只需要求出最优值,那么步骤(4)可以省略。若需要求出问题的一个最优解,则必须执行步骤(4),步骤(3)中记录的信息是构造最优解的基础。
1.3 动态规划解决0-1背包问题
问题描述:
某商店有n个物品,第i个物品价值为vi,重量(或权重)为wi,背包的容量为W。每种物品只能选择完全装入或不装入背包,一个物品至多装入一次,因此该问题被称为0-1背包问题。目标是如何选择装入背包的物品,使装入背包的物品总价值最大。
可将0-1背包问题描述为如下形式:
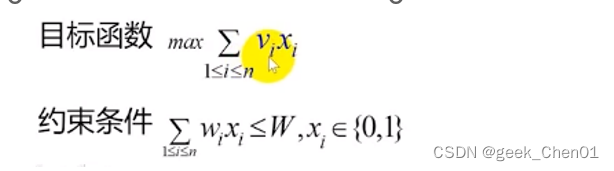
1.3.1求解步骤:


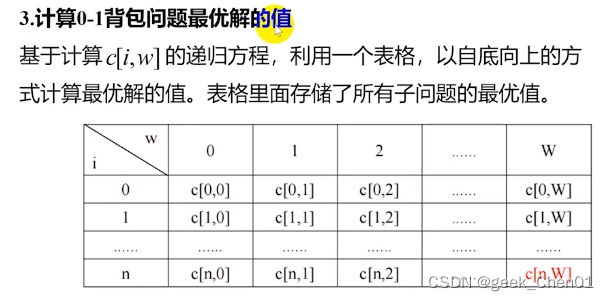
1.3.1.1个人理解:
步骤2:c[i,w]递归式;
第一个情况:没东西(i=0)/背包空间为0(w=0);
第二种情况:第i个东西比背包总容量大,装不下;只能考虑前i-1个东西来装;
第三种情况【第i个装/不装进去】:
装下第i个,这样少了wi![]() 个空间,但增加了vi
个空间,但增加了vi![]() 的价值;
的价值;
第i个东西可以不装(留着装前面i-1个物品中的某些);
取两个中最大值。【最大值即上一步的最优解】;【一定找的到最优解,但不一定所有最优解都找的完;比如这一步的价值是10;上一步是8和7;那么从上一步到这一步就是8+2=10,和7+3=10;我们考虑的每一步都求稳找到最优解,所以一定不会选7(即便他的最后一步是会+3到10)】
填表顺序:从左到右,从上到下;
1.3.2 伪代码实现_(3)最优值表的构建
KNAPSACK-DP(n, W)
for w <- 0 to W
do c[0, w] <- 0
for i <- 1 to n
do c[i, 0] <- 0
for w <- 1 to W
do if w[i] ≤ w
then if v[i] + c[i-l, w -w[i] ] > c[i-l, w]
then c[i, w] <- v[i]+ c[i-1, w-w[i] ]
else c[i, w] <- c[i-1, w]
else c[i, w] <- c[i-1, w]1.3.2.1个人理解:
1-4句:初始化;把左、上的边界给值为0;【没有东西/背包空间为0 –结果都是总价值v为0】
5句:开始计算表的内层;(注意还在3的大循环里)
6:如果第i个物品的重量wi![]() ≤背包的空间(w),即能装下;那么then:
≤背包的空间(w),即能装下;那么then:
7:比较装/不装两种情况的最大值;如果装了更大,then:
8:把这个最大值赋给c[i,w];
9:如果不装更大,那就不装,此时考虑前i个和考虑前i-1个的一样的情况;所以c[i-1,w]赋给了c[i,w];
10:对应6的if,如果装不下第i个,那就考虑前i-1个,同9;
计算最优值时间为 O(nW)--:时间来源于3,5句的 双重for循环;
1.3.3 伪代码实现_(4)求问题的最优解

1.3.3.1代码解释:
1句:循环i : n 到2 (downto 2是直到减到2的时候)
2:即判断,第i个是否对总价值c产生影响(没影响就是没装)
3:得出xi =0,没装;
4:else装了;
5:装了的情况下,减去消耗的空间;w= w-wi;
6:x1(第一个物品)的赋值【是边界,没法去比较第1个和第0个,所以单独拿出来说明】;语句即判断,if c[1,w] =1那么x为1,or为0;【c[1,w]即只考虑了第一个物品,那就要么装第一个,要么什么都没有;所以可以用0/1去判断】
7: return x 是一个01串,是个序列,代表每i个物品装/不装;
构造最优解的时间为 O(n)。
1.3.4 例题
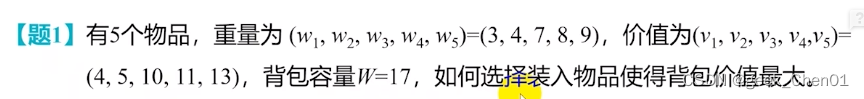
一般题目给出一个实际例子,要求解出递归方程c[i,w];求出结果--最优解;
1.3.4.1 最优值表
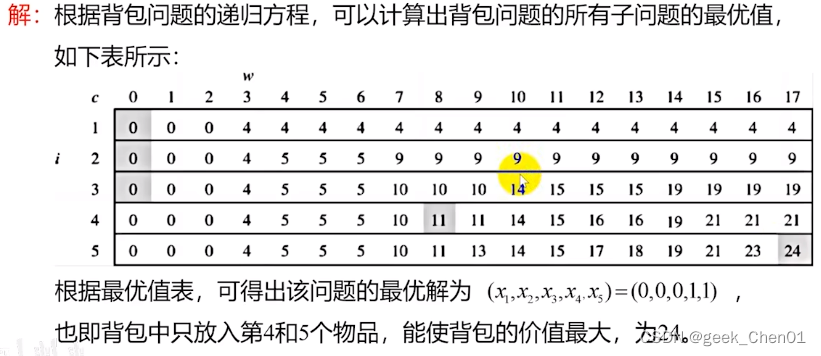
1.3.4.2 课件例题

【最大子段和没来得及看,不会,,,】