力扣周赛394之别样DP + 别样Dijkstra

别样DP

题目链接

https://leetcode.cn/problems/minimum-number-of-operations-to-satisfy-conditions/description/

题目大意

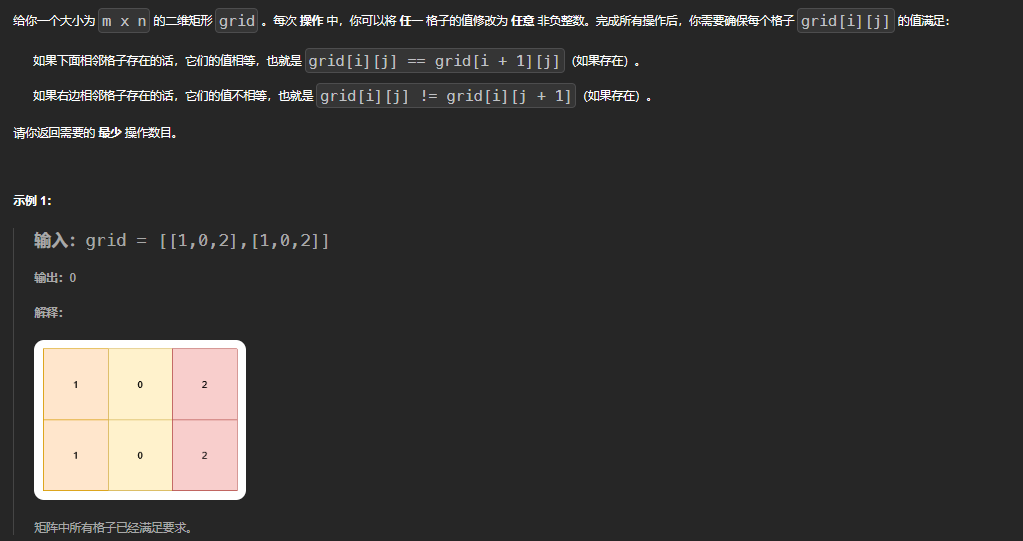
题目思路

• 需要考虑m列每一列填什么的情况，因为最终每一列都是一样的
• 考虑暴力，每一列都可以变成 0-9 有 \(10^m\) 次种情况，这必然是不可行的
• 我们从前往后看，后一列的情况不会影响前一列的情况
• dp应运而生，dp[i][x]表示第i列都变成x需要的最少操作数
• dp[i][x] = dp[i - 1][y] + n - cnt[x] 【其中 x != y】

题目代码

class Solution:
    def minimumOperations(self, grid: List[List[int]]) -> int:
        n,m = len(grid),len(grid[0])
        ans = 0
        cols = [[0 for _ in range(10)] for _ in range(m)]
        for j in range(m):
            for i in range(n):
                x = grid[i][j]
                cols[j][x] += 1
        dp = [[inf for _ in range(10)] for _ in range(m)]
        for x in range(10):
            dp[0][x] = n - cols[0][x]

        for i in range(1,m):
            for x in range(10):
                for y in range(10):
                    if x != y:
                        dp[i][y] = min(dp[i][y],dp[i - 1][x] + n - cols[i][y])
        return min(dp[-1])

别样Dijkstra

题目链接

https://leetcode.cn/problems/find-edges-in-shortest-paths/description/

题目大意

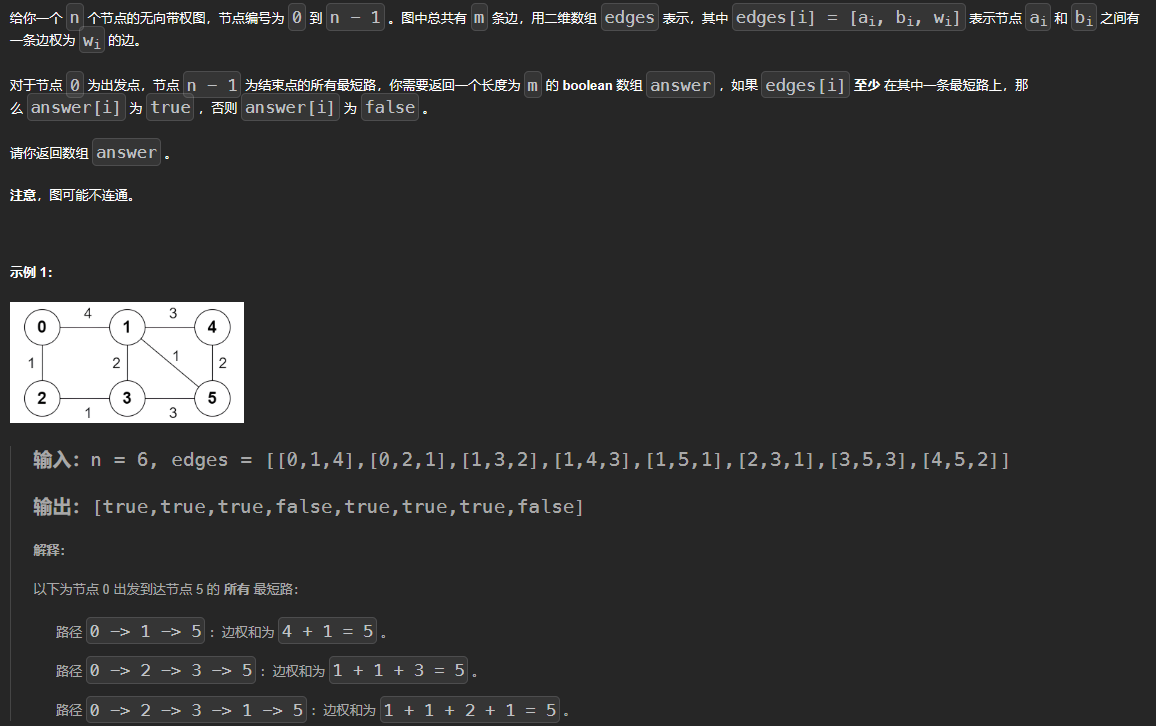
题目思路

设pre[v]表示最短路中可以转移到v的节点，且是u-v一定是最短路上的边！

• 考虑状态转移的情况
• ①dis[v] > dis[u] + w 【dis[v] = dis[u] + w】【v的最短距离被u更新】，所以pre[v] = [u]
• ②dis[v] = dis[u] + w 增加了一个可以转移到v的节点u, pre[v].append(u)

题目代码

class Solution:
    def findAnswer(self, n: int, edges: List[List[int]]) -> List[bool]:
        ans = [False]  * len(edges)
        g = [[]for _ in range(n + 1)]
        for u,v,w in edges:
            g[u].append([v,w])
            g[v].append([u,w])
        dis = [inf] * n
        dis[0] = 0
        heap = [(0,0)]
        pre = [[]for _ in range(n)]
        while heap:
            d,u = heappop(heap)
            if d > dis[u]:
                continue
            for v,w in g[u]:
                if dis[v] > d + w:
                    dis[v] = d + w
                    heappush(heap,(d + w,v))
                    pre[v] = [u]
                elif dis[v] == d + w:
                    pre[v].append(u)
        s = set()
        def dfs(v):
            for u in pre[v]:
                s.add((u,v))
                dfs(u)
        dfs(n - 1)
        for i,(u,v,_) in enumerate(edges):
            if (u,v) in s or (v,u) in s:
                ans[i] = True
        return ans