LCA + 树上倍增
LCA + 树上倍增
一、例题引入
题目:
现有一棵由 n 个节点组成的无向树,节点按从 0 到 n - 1 编号。给你一个整数 n 和一个长度为 n - 1 的二维整数数组 edges ,其中 edges[i] = [ui, vi, wi] 表示树中存在一条位于节点 ui 和节点 vi 之间、权重为 wi 的边。
另给你一个长度为 m 的二维整数数组 queries ,其中 queries[i] = [ai, bi] 。对于每条查询,请你找出使从 ai 到 bi 路径上每条边的权重相等所需的 最小操作次数 。在一次操作中,你可以选择树上的任意一条边,并将其权重更改为任意值。
注意:
- 查询之间 相互独立 的,这意味着每条新的查询时,树都会回到 初始状态 。
- 从
ai到bi的路径是一个由 不同 节点组成的序列,从节点ai开始,到节点bi结束,且序列中相邻的两个节点在树中共享一条边。
返回一个长度为 m 的数组 answer ,其中 answer[i] 是第 i 条查询的答案。
示例:
query[i] = [2,6],将2-3这条边改成2,所以ans[i] = 1
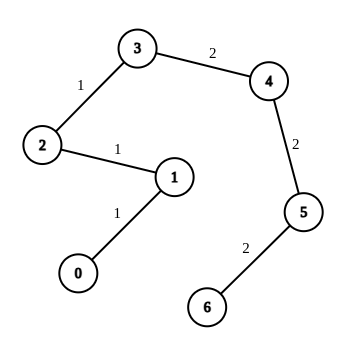
思路:
- ①求2到6的距离
d = 4; - ②求2到6边权出现次数最多的次数
cnt_max = 3; - ③答案即为:
d - cnt_max = 1
二、对症下药
①怎么快速求出一棵树上任意两个点的距离呢?
d(a-b) = d(a-lca) + d(b-lca) = (d(a-root) - d(lca-root)) + (d(b-root) - d(lca-root)) = d(a) + d(b) - 2 x d(lca)
只要求出最近公共祖先lca后,就可以根据如上公式求出任意两点的距离。
②怎么求公共祖先呢?
1.预处理pa数组
pa[x][0] = y代表 x 的父节点是y.
pa[x][1] = y 代表 x 的父节点的父节点是y.
pa[x][2] = y代表 x 的爷节点的爷节点是y.
依次类推..........................................................
pa[x][i + 1] = pa[pa[x][i]][i]
// 设 m 为最大编号的二进制位数,pa数组初始化为-1
for (int i = 0; i < m - 1; i++) {
for (int x = 0; x < n; x++) {
int p = pa[x][i];
if (p != -1) pa[x][i + 1] = pa[p][i];
}
}
2.二进制倍增
设x与y的最近公共祖先为lca,根节点为root
-
首先,使得
x与y在同一层- 如果在同一层时
x = y,那么lca = x = y
- 如果在同一层时
-
将
x与y按照i从大往小跳 \(2^i\)得到fx,fy(类比数的二进制表示)- 如果
fx = fy,就说明跳得太远了,(超过了lca或者就是lca)下一次就跳得近一些 - 如果
fx != fy,就说明在lca之下,那么更新x = fx,y = fy
- 如果
-
最后,得到的节点一定是
lca的儿子节点lca = pa[x][0]
if (depth[x] > depth[y]) swap(x, y);
// 让 y 和 x 在同一深度
for (int k = depth[y] - depth[x]; k; k &= k - 1) {
int i = __builtin_ctz(k);
int p = pa[y][i];
y = p;
}
if (y != x) {
// x 和 y 同时上跳 2^i 步
for (int i = m - 1; i >= 0; i--) {
int fx = pa[x][i], fy = pa[y][i];
if (fx != fy) {
x = fx;
y = fy;
}
}
x = pa[x][0];
}
lca = x;
③怎么求边权出现次数最多的那条边的次数呢?
1.定义cnt[x][i][w]数组
cnt[x][0][w] = 1 代表 x 与x父节点之间的路径的权值为w的边个数为1.
cnt[x][1][w] = 2 代表 x 与x爷节点之间的路径的权值为w的边个数为2.
cnt[x][i][w] = cnt代表 x 与x 跳\(2^i\) 后的节点的路径的权值为w的边个数为cnt.
只需在求LCA的过程中维护与更新cnt即可!
三、代码展示
class Solution {
public:
vector<int> minOperationsQueries(int n, vector<vector<int>> &edges, vector<vector<int>> &queries) {
vector<vector<pair<int, int>>> g(n);
for (auto &e: edges) {
int x = e[0], y = e[1], w = e[2] - 1;
g[x].emplace_back(y, w);
g[y].emplace_back(x, w);
}
int m = __lg(n) + 1; // n 的二进制长度
vector<vector<int>> pa(n, vector<int>(m, -1));
vector<vector<array<int, 26>>> cnt(n, vector<array<int, 26>>(m));
vector<int> depth(n);
function<void(int, int)> dfs = [&](int x, int fa) {
pa[x][0] = fa;
for (auto [y, w]: g[x]) {
if (y != fa) {
cnt[y][0][w] = 1;
depth[y] = depth[x] + 1;
dfs(y, x);
}
}
};
dfs(0, -1);
for (int i = 0; i < m - 1; i++) {
for (int x = 0; x < n; x++) {
int p = pa[x][i];
if (p != -1) {
pa[x][i + 1] = pa[p][i];
for (int j = 0; j < 26; ++j) {
cnt[x][i + 1][j] = cnt[x][i][j] + cnt[p][i][j];
}
}
}
}
vector<int> ans;
for (auto &q: queries) {
int x = q[0], y = q[1];
int path_len = depth[x] + depth[y]; // 最后减去 depth[lca] * 2
int cw[26]{};
if (depth[x] > depth[y]) {
swap(x, y);
}
// 让 y 和 x 在同一深度
for (int k = depth[y] - depth[x]; k; k &= k - 1) {
int i = __builtin_ctz(k);
int p = pa[y][i];
for (int j = 0; j < 26; ++j) {
cw[j] += cnt[y][i][j];
}
y = p;
}
if (y != x) {
for (int i = m - 1; i >= 0; i--) {
int fx = pa[x][i], fy = pa[y][i];
if (fx != fy) {
for (int j = 0; j < 26; j++) {
cw[j] += cnt[x][i][j] + cnt[y][i][j];
}
x = fx;y = fy; // x 和 y 同时上跳 2^i 步
}
}
for (int j = 0; j < 26; j++) {
cw[j] += cnt[x][0][j] + cnt[y][0][j];
}
x = pa[x][0];
}
int lca = x;
path_len -= depth[lca] * 2;
ans.push_back(path_len - *max_element(cw, cw + 26));
}
return ans;
}
};
四、实战演练
给定一棵包含 n个节点的有根无向树,节点编号互不相同,但不一定是 1∼n。
有 m个询问,每个询问给出了一对节点的编号 x 和 y,询问 x与 y 的祖孙关系。
输入格式
输入第一行包括一个整数 表示节点个数;
接下来 n行每行一对整数 a 和 b,表示 a 和 b 之间有一条无向边。如果 b是 −1−1,那么 a 就是树的根;
第 n+2 行是一个整数 m表示询问个数;
接下来 m 行,每行两个不同的正整数 x和 y,表示一个询问。
输出格式
对于每一个询问,若 x是 y的祖先则输出 1,若 y是 x的祖先则输出 2,否则输出 0。
代码撰写
#include<bits/stdc++.h>
using namespace std;
const int N = 40010, M = 2 * N;
int h[N], e[M], ne[M], idx;
int depth[N], pa[N][20],root;
void add(int a, int b)
{
e[idx] = b, ne[idx] = h[a], h[a] = idx ++;
}
//预处理每个结点的深度,以及结点的父结点的编号
void dfs(int u, int fa)
{
pa[u][0] = fa;
for(int i = h[u]; ~i; i = ne[i])
{
int v = e[i];
if(v != fa){
depth[v] = depth[u] + 1;
dfs(v,u);
}
}
}
int get_lca(int x,int y){
if(depth[x] > depth[y]) swap(x,y);
for(int k = depth[y] - depth[x];k;k &= k - 1){
int i = __builtin_ctz(k);
y = pa[y][i];
}
if(x == y) return y;
for(int i = 15;i >= 0;--i){
int fx = pa[x][i],fy = pa[y][i];
if(fx != fy){
x = fx;y = fy;
}
}
return pa[x][0];
}
int main()
{
ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);
memset(h, -1, sizeof(h));memset(pa,-1,sizeof(pa));
int t;cin >> t;
while(t--){
int a,b;cin >> a >> b;
if(b == -1) root = a;
else {add(a,b);add(b,a);}
}
dfs(root,-1);
for(int i = 0;i < 15;++i){
for(int u = 0;u < N;++u){
int p = pa[u][i];
if(p != -1) pa[u][i + 1] = pa[p][i];
}
}
cin >> t;
while(t--){
int a,b;cin >> a >> b;
int lca = get_lca(a,b);
if (lca == a) cout << '1' << '\n';
else if(lca == b) cout << '2' << '\n';
else cout << '0' << '\n';
}
return 0;
}




 浙公网安备 33010602011771号
浙公网安备 33010602011771号