背包DP
一、01背包
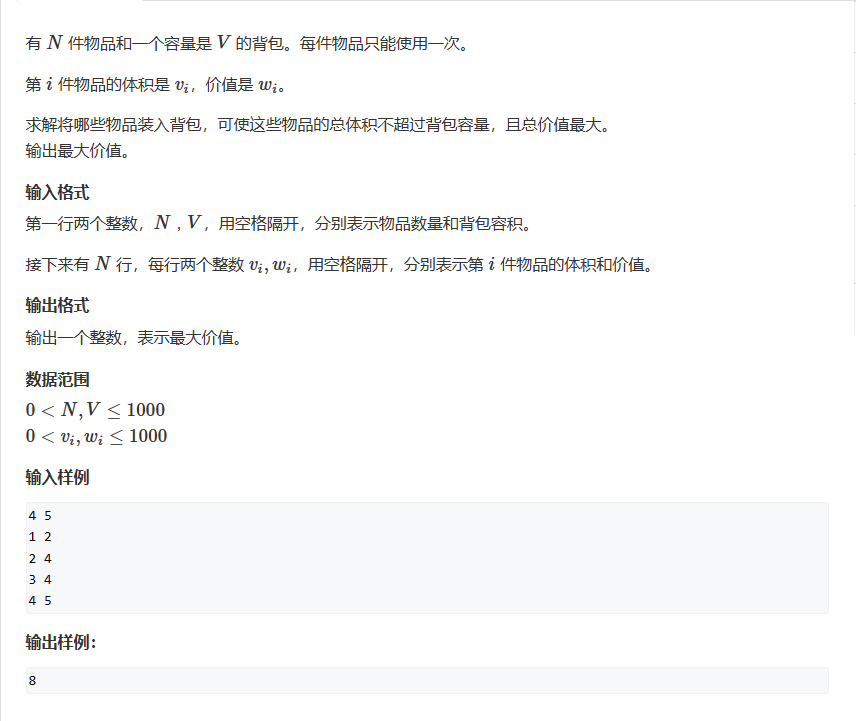
定义dp[i][j]表示从前i件物品中选,体积不超过 j 的最大价值
N, V = map(int, input().split())
v = [0] * (N + 1)
w = [0] * (N + 1)
for i in range(1,N + 1):
v[i],w[i] = map(int,input().split())
f = [[0] * (V + 1) for _ in range(N + 1)]
# 对于第i件物品,选或不选!
for i in range(1, N + 1):
for j in range(V, -1, -1):
if j < v[i]:
f[i][j] = f[i - 1][j]
else:
f[i][j] = max(f[i - 1][j], f[i - 1][j - v[i]] + w[i])
print(f[N][V])
变式1
如果改为定义dp[i][j]表示从前i件物品中选,体积恰好为 j 的最大价值,该如何?
答:只需将dp[0][0]设为0,其余的全设为inf即可
变式2
如果要求改进空间复杂度,该如何?
答:滚动数组或省去第一维度的空间【体积得从大到小枚举,防止使用更新后的数据】
变式3
如果让你求使价值最大的方案数,该如何?
答:用一个cnt数组,统计方案数,主要在更新dp[j]的那里更新cnt[j]【注意这里变成体积恰好为j的情况】
from math import inf
MOD = pow(10,9) + 7
N, V = map(int, input().split())
v = [0] * (N + 1)
w = [0] * (N + 1)
for i in range(1,N + 1):
v[i],w[i] = map(int,input().split())
dp = [-inf] * (V + 1)
dp[0] = 0
cnt = [0] * (V + 1)
cnt[0] = 1
# 对于第i件物品,选或不选!
mx = 0
for i in range(1, N + 1):
for j in range(V, v[i] - 1, -1):
if dp[j] == dp[j - v[i]] + w[i]:
cnt[j] += cnt[j - v[i]]
elif dp[j] < dp[j - v[i]] + w[i]:
cnt[j] = cnt[j - v[i]]
dp[j] = dp[j - v[i]] + w[i]
cnt[j] %= MOD
mx = max(mx,dp[j])
ans = 0
for i in range(V + 1):
if dp[i] == mx:
ans = (ans + cnt[i]) % MOD
print(ans)
变式4
如果让你求一个具体的方案[要求字典序最小],该如何?
答:只需往回推即可,也即判断dp[i][j] == dp[i + 1][j - v[i]] + w[i],看是否满足,满足就一定可以!
N, V = map(int, input().split())
v = [0] * (N + 1)
w = [0] * (N + 1)
for i in range(1,N + 1):
v[i],w[i] = map(int,input().split())
dp = [[0 for _ in range(V + 1)]for _ in range(N + 2)]
for i in range(N,0,-1):
for j in range(V + 1):
if j >= v[i]:
dp[i][j] = max(dp[i + 1][j],dp[i + 1][j - v[i]] + w[i])
else:
dp[i][j] = dp[i + 1][j]
ans = []
for i in range(1,N + 1):
if V >= v[i] and dp[i][V] == dp[i + 1][V - v[i]] + w[i]:
ans.append(i)
V -= v[i]
print(*ans)
二、完全背包
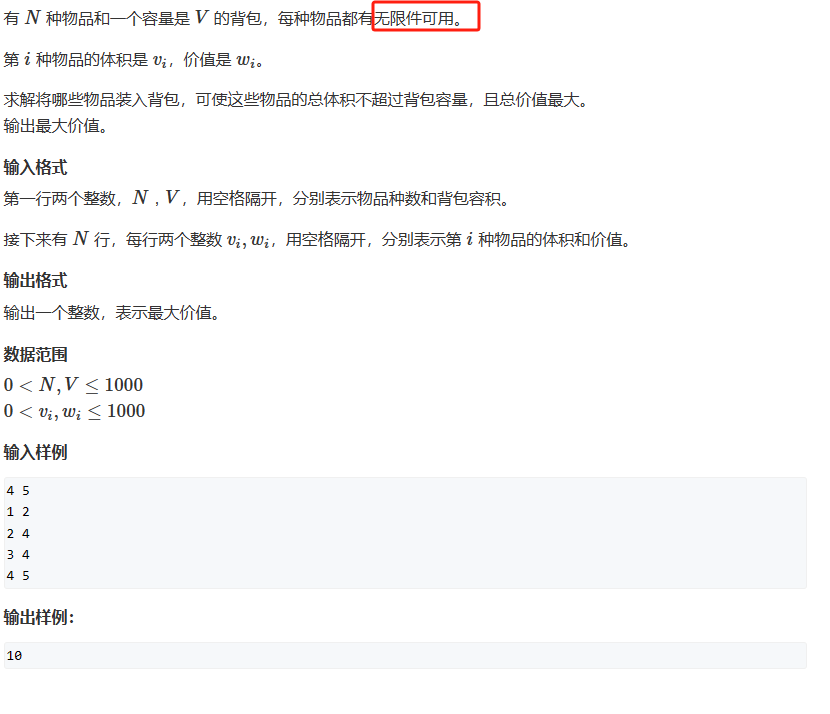
定义dp[i][j]表示从前i件物品中选,体积不超过 j 的最大价值
只不过对于每一件物品,可以选很多次!
二维版本
N,V = map(int,input().split())
dp = [[0] * (V + 1) for _ in range(N + 1)]
v = [0] * (N + 1)
w = [0] * (N + 1)
for i in range(1,N + 1):
v[i],w[i] = map(int,input().split())
for i in range(1,N + 1):
for j in range(V + 1):
if j < v[i]:
dp[i][j] = dp[i - 1][j]
else:
# 选或不选,只不过与01背包不同的是dp[i][j - v[i]] + w[i],可以选多次i!
dp[i][j] = max(dp[i - 1][j],dp[i][j - v[i]] + w[i])
print(dp[N][V])
一维版本
N,V = map(int,input().split())
dp = [0] * (V + 1)
v = [0] * (N + 1)
w = [0] * (N + 1)
for i in range(1,N + 1):
v[i],w[i] = map(int,input().split())
for i in range(1,N + 1):
for j in range(v[i],V + 1):
# 与01背包不同的是,这里不用逆序枚举,因为需要用到更新后的状态,选择多个i
dp[j] = max(dp[j],dp[j - v[i]] + w[i])
print(dp[V])
三、多重背包

方案一
直接枚举个数
方案二
二进制枚举
方案三
单调队列优化
如果一共有3个物品,即s=3,那么dp[3*v+1]的最大值为
dp[3*v+1]=max(pre[3*v+1],pre[2*v+1]+w,pre[v+1]+2w,pre[1]+3w);
-----------------------------------------------------------------------------
于是,我们可以得到下列算式:(其中r表示余数)
dp[r] = pre[r];
dp[r+v] = max(pre[r]+ w,pre[r+v]);
dp[r+2v]= max(pre[r]+2w,pre[r+v]+w, pre[r+2v],);
dp[r+3v]= max(pre[r]+3w,pre[r+v]+2w,pre[r+2v]+w,g[r+3v]);
···
dp[r+sv]=max(pre[r]+sw,···,pre[r+(s-1)v]+w,pre[r+sv]);
-----------------------------------------------------------------------------
转换
dp[r] = pre[r];
dp[r+v] = max(pre[r],pre[r+v]-w)+w;
dp[r+2v]= max(pre[r],pre[r+v]-w,pre[r+2v]-2w)+2w;
dp[r+3v]= max(pre[r],pre[r+v]-w,pre[r+2v]-2w,pre[r+3v]-3w)+3w;
···
dp[r+sv]= max(pre[r],···,pre[r+(s-1)v]-(s-1)w,pre[r+sv]-sw)+sw;
-----------------------------------------------------------------------------
from collections import deque
N,V = map(int,input().split())
dp = [0] * (V + 1)
for i in range(1,N + 1):
v,w,s = map(int,input().split())
pre = dp[:]
for r in range(v):
q = deque()
for j in range(r,V + 1,v):
while q and (j - q[0]) // v > s:
q.popleft()
# pre[q[-1]] - (q[-1] - r) // v * w <= pre[j] - (j - r) // v * w
while q and pre[q[-1]] + (j - q[-1]) // v * w <= pre[j]:
q.pop()
q.append(j)
# pre[q[0]] - (q[0] - r) // v * w + (j - r) // v * w
dp[j] = pre[q[0]] + (j - q[0]) // v * w
print(dp[V])
四、混合背包
将上述完全背包与多重背包通过二进制的转换变成01背包即可!

五、二维费用的背包
加一维即可,换汤不换药

六、分组背包

如法炮制,在每一个组内枚举选哪个即可!
N,V = map(int,input().split())
dp = [0] * (V + 1)
for i in range(1,N + 1):
s = int(input())
v = [0] * (s + 1)
w = [0] * (s + 1)
for j in range(1,s + 1):
v[j],w[j] = map(int,input().split())
for j in range(V,-1,0):
# 枚 举 组 内 选 哪 个 ?
for k in range(1,s + 1):
if j >= v[k]:
dp[j] = max(dp[j],dp[j - v[k]] + w[k])
print(dp[V])
七、有依赖的背包问题[树形DP]
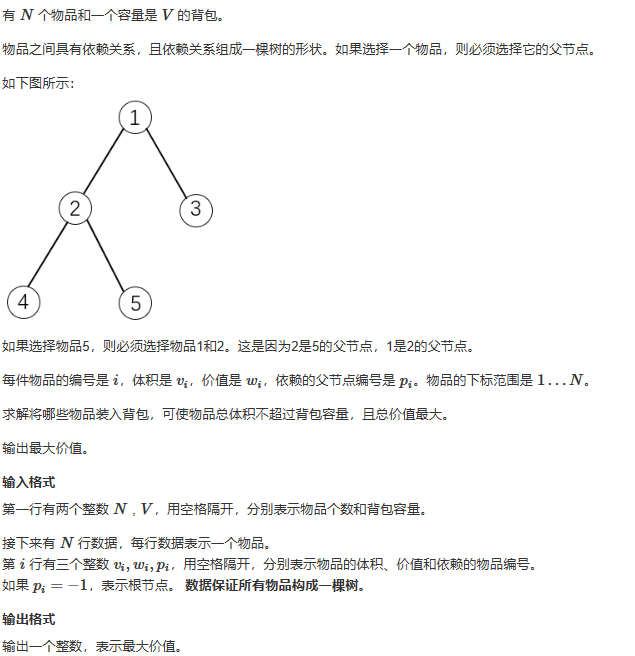
N, V = map(int, input().split())
# dp[i][j] 表 示 以 i 为 根 节 点,体 积 不 超 过 j 的 最 大 价 值 !
# 整个dp其实优化了一维,本质上是dp[i][k][j]表示以i为根节点,从前k个子树选择,体积不超过j的最大价值!(分组背包)
dp = [[0] * (V + 1) for _ in range(N + 1)]
v = [0] * (N + 1)
w = [0] * (N + 1)
g = [[] for _ in range(N + 1)]
root = None
for i in range(1, N + 1):
v[i], w[i], pa = map(int, input().split())
if pa == -1:
root = i
else:
g[pa].append(i)
def dfs(x):
for j in range(v[x],V + 1):
dp[x][j] = w[x]
for y in g[x]:
dfs(y)
for j in range(V,v[x] - 1, -1):
for k in range(j - v[x] + 1):
dp[x][j] = max(dp[x][j], dp[x][j - k] + dp[y][k])
dfs(root)
print(dp[root][V])
贴一个别人未优化前的代码
#include <cstdio>
#include <cstring>
#include <iostream>
#include <algorithm>
#include <vector>
using namespace std;
const int N=110;
vector<int> son[N]; //用来存储每个节点的子节点
int v[N],w[N];
int f[N][N][N];
int n,m;
void dfs(int x){
//进行初始化,当体积小于v[x]的时候是0,大于等于v[x]的时候是w[x]
for(int j=v[x];j<=m;j++) f[x][0][j]=w[x];
//下面进行分组背包,从前i个子树中选,总体积不超过j的所有集合,属性max
for(int i=1;i<son[x].size();i++){
int u=son[x][i];
int u_son=son[u].size()-1;
dfs(u);
for(int j=v[x];j<=m;j++){ //这里从v[x]开始,因为至少要包含x根节点
for(int k=0;k<=j-v[x];k++){ //这里要k<=j-v[x]是因为根节点必须包含,要给根节点留空间
f[x][i][j]=max(f[x][i][j],f[x][i-1][j-k]+f[u][u_son][k]);
}
}
}
}
int main(){
cin>>n>>m;
int root;
for(int i=1;i<=n;i++) son[i].push_back(0); //将下标改成从1开始,方便后面运算
for(int i=1;i<=n;i++){
int p;
cin>>v[i]>>w[i]>>p;
if(p==-1) root=i;
else son[p].push_back(i);
}
dfs(root);
cout<<f[root][son[root].size()-1][m]<<endl;
return 0;
}
作者:小虎成员
链接:https://www.acwing.com/solution/content/102500/
来源:AcWing




 浙公网安备 33010602011771号
浙公网安备 33010602011771号