动态规划法求解背包问题原理思路

一、什么是背包问题

0/1背包：有N件物品和一个最多能背重量为W 的背包。第i件物品的重量是weight[i]，得到的价值是value[i] 。每件物品只能用一次，求解将哪些物品装入背包里物品价值总和最大。

 

二、动态规划法求解0/1背包问题思路

　　每一件物品其实只有两个状态，取或者不取，所以可以使用回溯法搜索出所有的情况，那么时间复杂度就是O(2^n)，这里的n表示物品数量，这是指数级别的复杂度，显然是不可接受的。利用动态规划法求解能大大降低时间复杂度。

       物品从0开始编号，用i表示，背包的容量用j表示，确定动态规划的数组为dp[i][j]， 表示从下标为0~i的物品里任意取，放进容量为j的背包，价值总和最大是多少。那么在每次遍历到当前物品i的时候，无非就是两种情况，一种就是放了物品i后价值最大，一种是不放物品i价值最大，所以放不放物品i就看哪个价值最大即可，如下所示：

 三、案例解析

　　　　假设有3个物品，分别编号为0,1,2，求解的目标是在背包容量为4的情况下，所能达到的最大价值是多少？如下图：

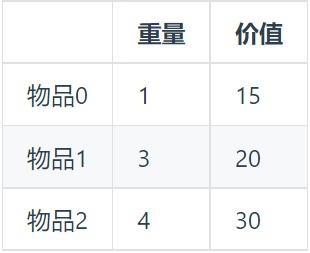
整体思路：先遍历物品从0~2，再遍历背包容量从0~4，整个遍历完就知道在背包容量为4的情况下的，最大价值是多少了。

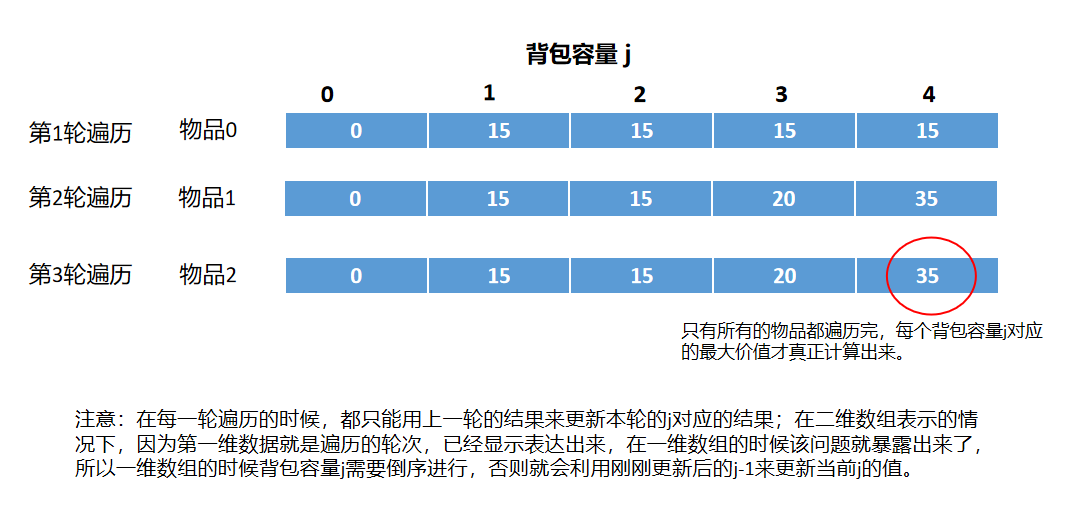
二维数组表示的代码：

def test_2_wei_bag_problem1(bag_size, weight, value) -> int: 
    rows, cols = len(weight), bag_size + 1
    dp = [[0 for _ in range(cols)] for _ in range(rows)]
    
    # 初始化dp数组. 
    for i in range(rows): 
        dp[i][0] = 0
    first_item_weight, first_item_value = weight[0], value[0]
    for j in range(1, cols):     
        if first_item_weight <= j: 
            dp[0][j] = first_item_value

    # 更新dp数组: 先遍历物品, 再遍历背包. 
    for i in range(1, len(weight)): 
        cur_weight, cur_val = weight[i], value[i]
        for j in range(1, cols): 
            if cur_weight > j: # 说明背包装不下当前物品. 
                dp[i][j] = dp[i - 1][j] # 所以不装当前物品. 
            else: 
                # 定义dp数组: dp[i][j] 前i个物品里，放进容量为j的背包，价值总和最大是多少。
                dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - cur_weight]+ cur_val)

    print(dp)

一维数组表示的代码

def test_1_wei_bag_problem():
    weight = [1, 3, 4]
    value = [15, 20, 30]
    bag_weight = 4
    # 初始化: 全为0
    dp = [0] * (bag_weight + 1)

    # 先遍历物品, 再遍历背包容量
    for i in range(len(weight)):
        #倒序遍历，避免使用本轮的刚刚更新的j-weight[i],倒序的时候就只能使用上一轮的。容量j倒序只需要遍历与当前物品i一样的重量即可，
       再小也没有必要遍历了，肯定放不下i
        for j in range(bag_weight, weight[i] - 1, -1):
            # 递归公式
            dp[j] = max(dp[j], dp[j - weight[i]] + value[i])

    print(dp)

 

四、可以选择用贪心算法来解决0/1背包问题吗？

    既然每一种物品都有价格和重量，我们优先挑选那些单位价格最高的是否可行呢？比如在下图中，背包的容量是50kg，我们有3种物品，他们的重量和价格分别是10, 20, 30 kg和60, 100, 120。

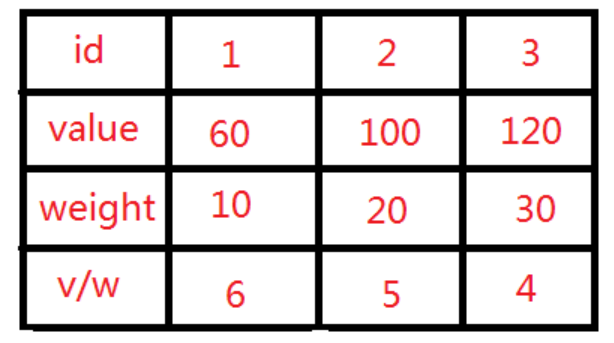
      那么按照单位价格来算的话，我们最先应该挑选的是价格为60的元素，选择它之后，背包还剩下50 - 10 = 40kg。再继续前面的选择，我们应该挑选价格为100的元素，这样背包里的总价值为60 + 100 = 160。所占用的重量为30, 剩下20kg。因为后面需要挑选的物品为30kg已经超出背包的容量了。我们按照这种思路能选择到的最多就是前面两个物品，总价值160。

       按照我们前面的期望，这样选择得到的价值应该是最大的。可是由于有一个背包重量的限制，这里只用了30kg，还有剩下20kg浪费了。这会是最优的选择吗？我们看看所有的选择情况：

 

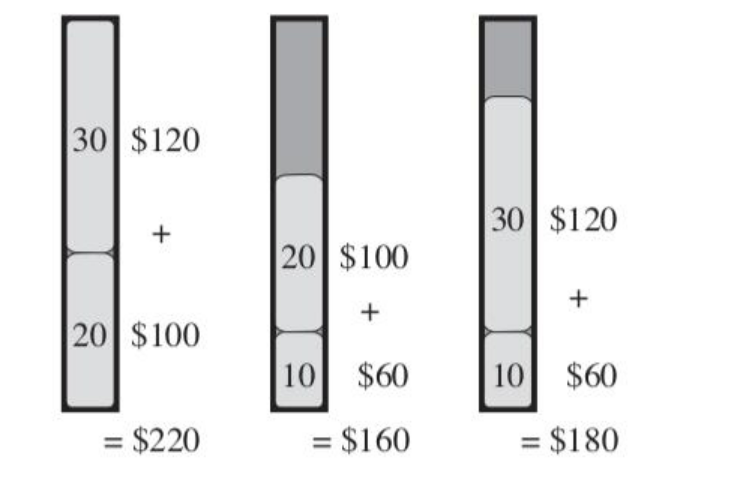
　　对于0-1背包问题，贪心选择之所以不能得到最优解是因为：它无法保证最终能将背包装满，部分闲置的背包空间使每公斤背包空间的价值降低了。

       但是对于背包问题是可以选择贪心算法的，背包问题：与0-1背包问题类似，所不同的是在选择物品i装入背包时，可以选择物品的一部分，而不一定要全部装入背包。对于背包问题而言，执行尽量装入最大单位重量价值的贪心选择即可

       事实上，在考虑0-1背包问题时，应比较选择该物品和不选择该物品所导致的最终方案，然后再作出最好选择。由此就导出许多互相重叠的子问题。这正是该问题可用动态规划算法求解的另一重要特征。

 

参考链接：代码随想录