实现求平方根sqrt(x)

一、二分查找法

对于一个非负数n，它的平方根不会小于大于（n/2+1）。在[0, n/2+1]这个范围内可以进行二分搜索，求出n的平方根。

int sqrt(int x) {
 2     long long i = 0;
 3     long long j = x / 2 + 1;
 4     while (i <= j)
 5     {
 6         long long mid = (i + j) / 2;
 7         long long sq = mid * mid;
 8         if (sq == x) return mid;
 9         else if (sq < x) i = mid + 1;
10         else j = mid - 1;
11     }
12     return j;

二、牛顿迭代法

牛顿迭代法原理如下：

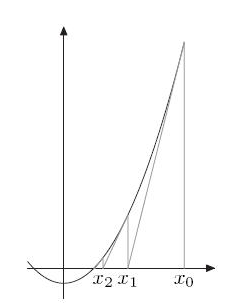
      计算x² = A的解，令f(x)=x²-A，相当于求解f(x)=0的解，如左图所示

      首先找到一个x0初始点，如果x0不是最优解，那求出经过点x0的切线，更新x0为x1，x1就是该切线与x轴的交点。

      继续迭代，x会向最优解不停的逼近。

     收敛条件有两种：1）是直接计算f(x_i)的值判断是否为0；2）判断前后两个解x_i和x_i-1是否无限接近。 

  

 代码如下：

def sqrt(x):
    if x==0:
        return 0
    last=0.0
    res=1.0
    while last!=res:#如果找到了根值，res就不再变化了，例如（3+9/3）/2=3,所以以此为收敛结束条件
        last=res
        res=(res+x/res)/2
    
    return res

参考：https://www.cnblogs.com/qlky/p/7735145.html