拉格朗日对偶理解

在约束最优化问题中，常常利用拉格朗日对偶性（Lagrange duality）将原始问题转换为对偶问题，通过解对偶问题而得到原始问题的解。这是因为：

1）对偶问题的对偶是原问题；

2）无论原始问题与约束条件是否是凸的，对偶问题都是凹问题，加个负号就变成凸问题了，凸问题容易优化。

3）对偶问题可以给出原始问题一个下界；

4）当满足一定条件时，原始问题与对偶问题的解是完全等价的；

 

原始问题：

       假设f(x),ci(x),hj(x)是定义在Rn上的联系可微函数，考虑约束条件下最优化问题：

       

称此约束最优化问题为原始问题。

 

广义拉格朗日函数：

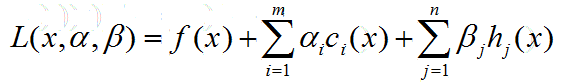
这里，x=(x1,x2,...,xn), α，β是拉格朗日乘子。

 

Lagrange对偶函数：

定义拉格朗日对偶函数或者对偶函数g为拉格朗日函数关于x取得的最小值，即对α，β，有：

 

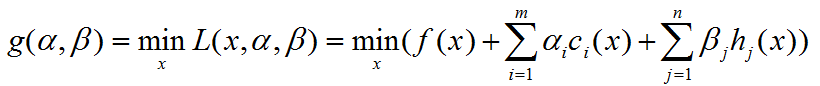
通俗理解就是每确定一组(α，β)，就要找到一个x使得L最小，不同的(α，β)对应不同的g函数值。

 

对偶函数与原问题的关系：

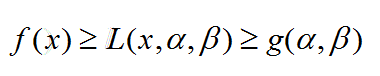
所以对偶函数是原问题的最优值下界，虽然不等式成立，但是如果α<0,并且让α趋近于负无穷，这个时候g(α,β)=-∞，虽然也满足不等式，但是此时没有任何意义。所以只有当α≥0，这个时候g(α,β)＞-∞时，对偶函数才能给出原目标函数一个非平凡有意义的下界，称此条件下的(α,β)是对偶可行的。图示如下：

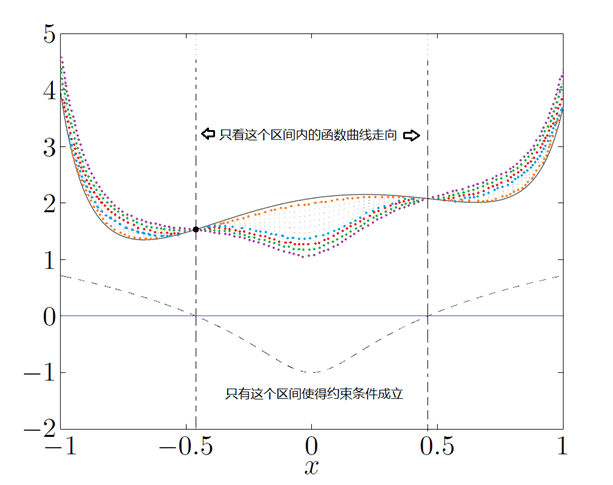
在图中，实线代表的是目标函数f(x)，而虚线代表的是约束条件c(x)，彩色的点线代表λ取不同值的时候对应的拉格朗日函数L。我们可以看到，在约束条件可行(c(x)≤0)的区间内，拉格朗日函数都是小于目标函数的。在可行区间内，目标函数的最值将在x = -0.46处取得p∗=1.54。

 

为什么对偶函数一定是凹函数呢？

 其实L可以理解为一个以固定x带入c(x)和h(x)作为常数值系数，α、β作为变量的仿射函数。

所谓仿射函数，就是f(x)=a*x+b形式，其实就是线性函数了。

所以，g(α,β)为很多个仿射函数的逐个x取值点取最小值：

 L=Aα+Bβ+C      其中：A=c(x)    B=h(x)    C=f(x)

例如：L=2α+3β+1，L=α+2β+4， L=5α+β+3等等。便于理解，先不考虑β，这样大致展示的图像就是如下：

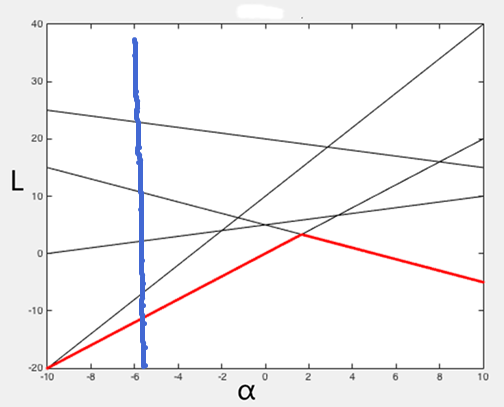
里面的每一条直线，都是以某一固定x作为系数，α作为变量的线性函数的直线，也就是当x固定时候，随着α的变化，L的值不断发生变化。

当我们沿着L所在轴竖着切下来的时候，也就是图中个蓝色线，这个时候其实就是α固定，而对应不同的x情况下，L值的一个变化范围。由图可知，红色线就是每次固定α，而找到一个x，使得L最小的走势线，也就是g(α,β)的函数曲线，如下图：

 

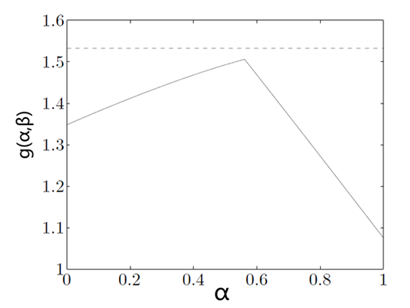
凹折线就是g(α,β)的曲线，水平虚线就是原问题的最优函数值P*。由此可知，无论原问题和约束条件是什么样的，对偶函数都是凹函数，且都小于等于原问题最优值。

 

 Lagrange对偶问题：

对于任意一组(α，β)，其中α≥0，拉格朗日对偶函数给出了原问题的最优值的一个下界，因此，我们可以得到和参数α，β相关的一个下界。一个自然问题是：从Lagrange函数能得到的最好下界是什么？可以将这个问题表述为优化问题：

 

上述问题就称之为Lagrange对偶问题。

前面讲只有当α≥0，g(α,β)＞-∞时此时才有意义，满足这样一组条件的(α，β)是上述对偶问题的一个可行解。如果一个解（α*，β*)是上述对偶问题的最优解，则称解(α*，β*)是对偶最优解或者最优Lagrange乘子。

此时对偶问题是一个凸优化问题，这是因为极大化目标函数是一个凹函数，且约束集合是一个凸集。

 

弱对偶

Lagrange对偶问题的最优值，我们用d*表示，根据定义，这是通过Lagrange函数得到的原问题最优值p*的最好下界。特别地，我们有下面简单但是非常重要的不等式

      

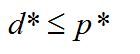
即使原问题不是凸问题，上述不等式也成立，这个性质称为弱对偶性。

 

强对偶性

与弱对偶性相对应的有一个强对偶性（strong duality） ，强对偶即满足：

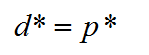
强对偶是一个非常好的性质，因为在强对偶成立的情况下，可以通过求解对偶问题来得到原始问题的解，在 SVM 中就是这样做的。当然并不是所有的对偶问题都满足强对偶性 ，在 SVM 中是直接假定了强对偶性的成立，其实只要满足一些条件，强对偶性是成立的，比如说 Slater 条件与KKT条件。

 

KKT条件：

 假设x*是原始问题的最优解，α*和β*是对偶问题的最优解。如果强对偶成立，那么原问题最优解和对偶问题最优解必须满足KKT条件，属于充分必要条件。