树

二叉搜索树

同时解决了有序数组插入时大量数据搬移和有序链表查找时间复杂度O(n)的问题。

二叉搜索树经过多次插入删除后，可能退化为链表，导致查找时间复杂度退化为O(n)。

平衡二叉树

二叉搜索树加入查找和删除的平衡算法，使每个节点的左子树高度和右子树高度差绝对值不超过1，形成平衡二叉树。

但旋转操作可能涉及大范围的指针重新赋值。

B树

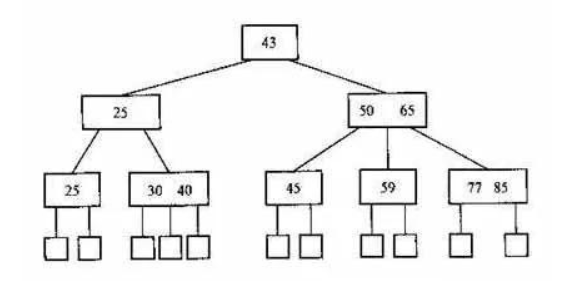
多路平衡查找树，也叫B-树。

B树的搜索，从根结点开始，对结点内的关键字（有序）序列进行二分查找，如果命中则结束，否则进入查询关键字所属范围的儿子结点；

重复，直到所对应的儿子指针为空，或已经是叶子结点。

B树只能通过中序来遍历。

B树的特性：

1. 数据集合分布在整颗树中；

2. 任何一个数据出现且只出现在一个结点中；

3. 搜索有可能在非叶子结点结束；

4. 其搜索性能等价于在关键字全集内做一次二分查找；

5. 自动层次控制；

B+树

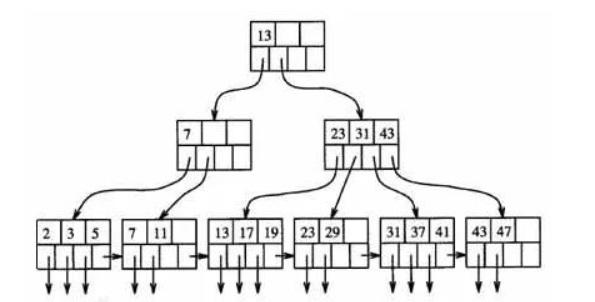
B+树是B树的变体，也是一种多路平衡查找树：

B+的搜索与B-树也基本相同，区别是B+树只有达到叶子结点才命中（B-树可以在非叶子结点命中），其性能也等价于在关键字全集做一次二分查找；

B+树的特性：

1. 所有数据都出现在叶子结点的链表中，且恰好是有序的；

2. 不可能在非叶子结点命中；

3. 非叶子结点相当于是叶子结点的索引，叶子结点相当于是存储（关键字）数据的数据层；

B+树相比B树的好处：

这样做的好处是：

1. 范围查询时可以通过访问叶子节点的链表进行有序遍历，而不再需要中序回溯访问结点。

2. 非叶子结点只存储关键字key，同一个页可以存储更多的关键字，读取单个页就可以得到更多的关键字，可检索的范围变大了，树的高度就降低了。

红黑树

是一种自平衡二叉搜索树

红黑树是不符合AVL树的平衡条件的，即每个节点的左子树和右子树的高度最多差1的二叉查找树。但是提出了为节点增加颜色，红黑树是用非严格的平衡来换取增删节点时候旋转次数的降低，任何不平衡都会在三次旋转之内解决，而AVL是严格平衡树，因此在增加或者删除节点的时候，根据不同情况，旋转的次数比红黑树要多。所以红黑树的插入效率更高

2、红黑树能够以O(log2 (n)) 的时间复杂度进行搜索、插入、删除操作

3、简单来说红黑树就是为了解决二叉查找树的缺陷，因为二叉查找树在某些情况下会退化成一个线性结构。