C++——二叉搜索树——数据结构进阶——附加超详细解析过程/代码完成


一、 二叉搜索树的介绍
⼆叉搜索树⼜称⼆叉排序树,它或者是⼀棵空树,或者是具有以下性质的⼆叉树:
• 若它的左⼦树不为空,则左⼦树上所有结点的值都⼩于等于根结点的值
• 若它的右⼦树不为空,则右⼦树上所有结点的值都⼤于等于根结点的值
• 它的左右⼦树也分别为⼆叉搜索树
• ⼆叉搜索树中可以⽀持插⼊相等的值,也可以不⽀持插⼊相等的值,具体看使⽤场景定义,后续我
们学习map/set/multimap/multiset系列容器底层就是⼆叉搜索树,其中map/set不⽀持插⼊相等
值,multimap/multiset⽀持插⼊相等值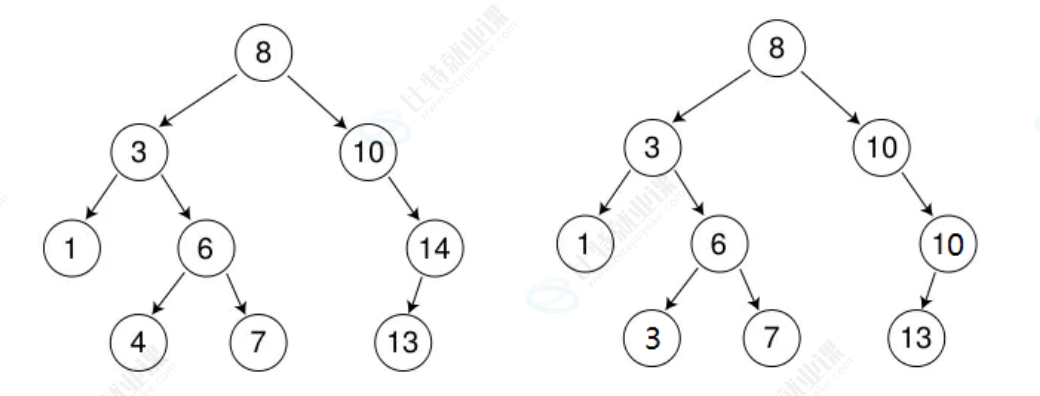
简化为 左<根 右>根
如果数值相等的情况下 默认生在右节点上
二叉搜索树的性能分析
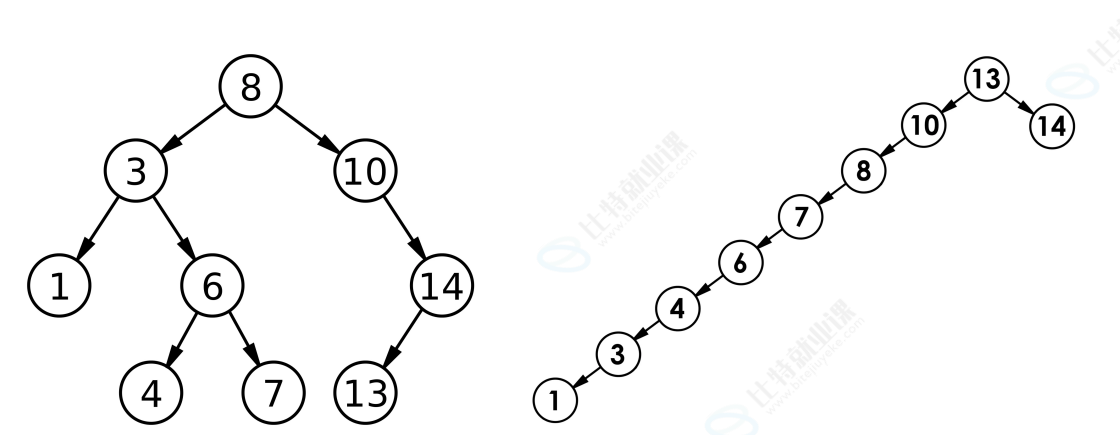
最优情况下,⼆叉搜索树为完全⼆叉树(或者接近完全⼆叉树),其⾼度为:log2N
最差情况下,⼆叉搜索树退化为单⽀树(或者类似单⽀),其⾼度:N
所以综合⽽⾔⼆叉搜索树增删查改时间复杂度为:O(N)
那么这样的效率显然是⽆法满⾜我们需求的,我们后续课程需要继续讲解⼆叉搜索树的变形,平衡⼆叉搜索树AVL树和红⿊树,才能适⽤于我们在内存中存储和搜索数据。
二、二叉树实现过程
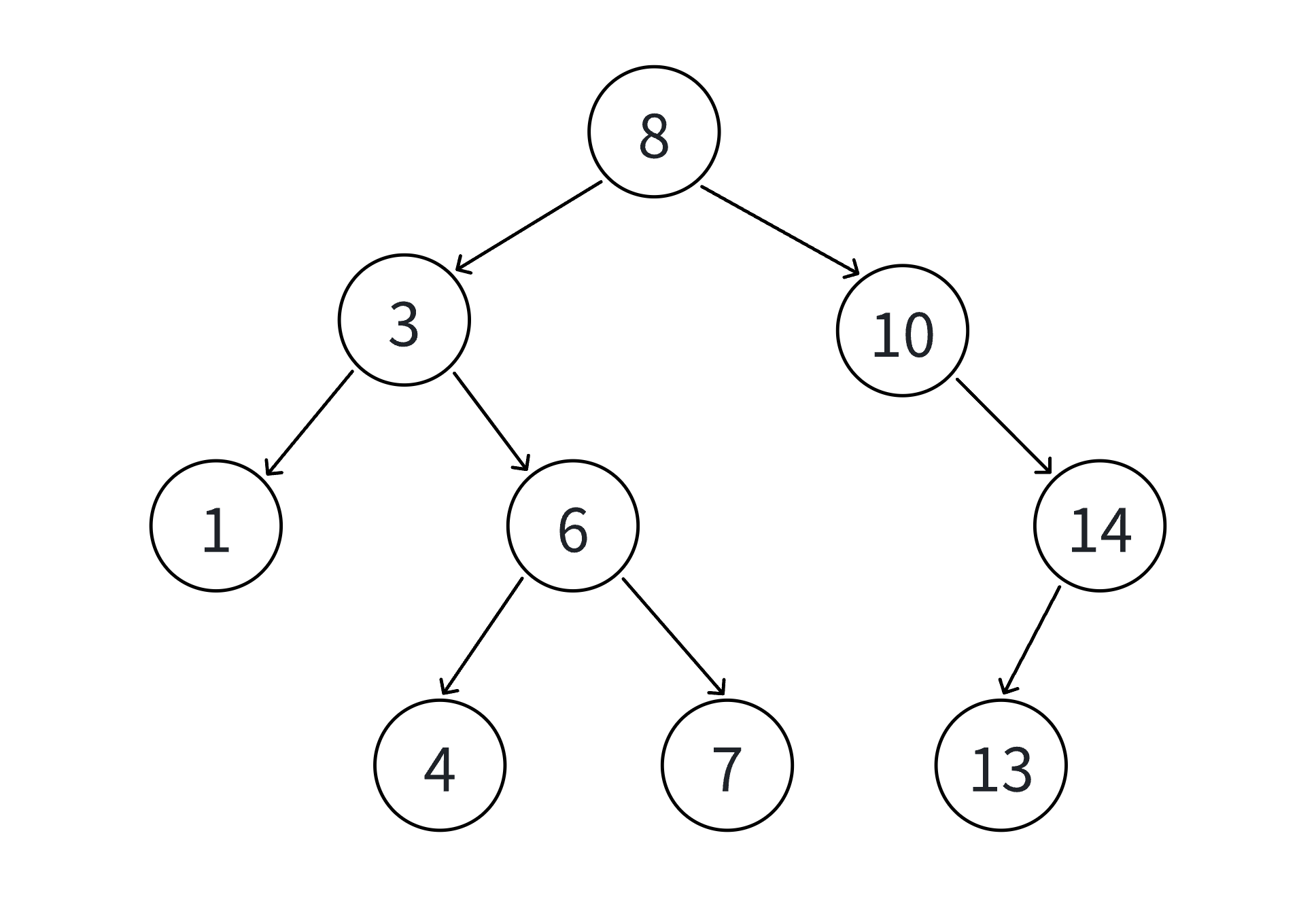
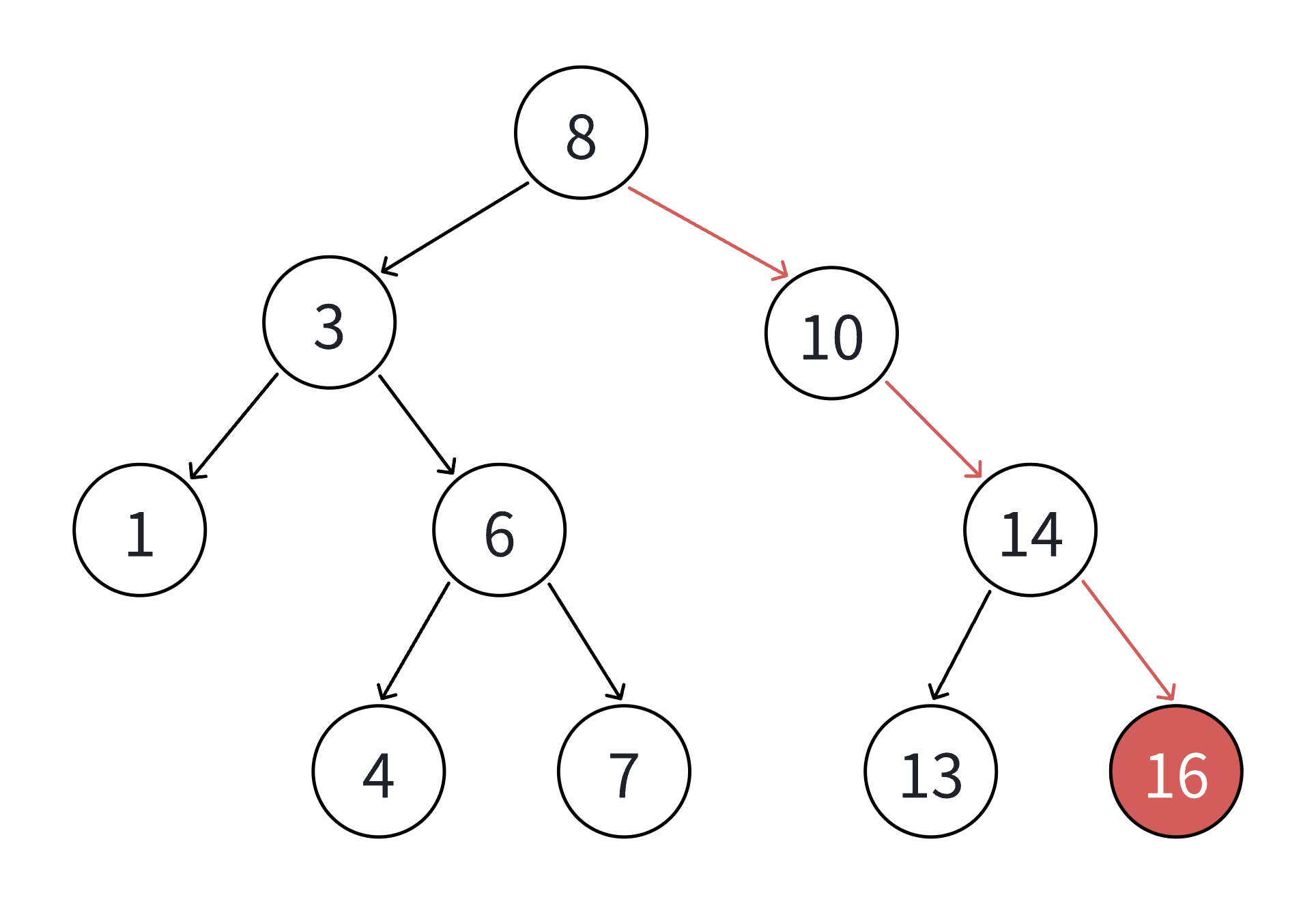
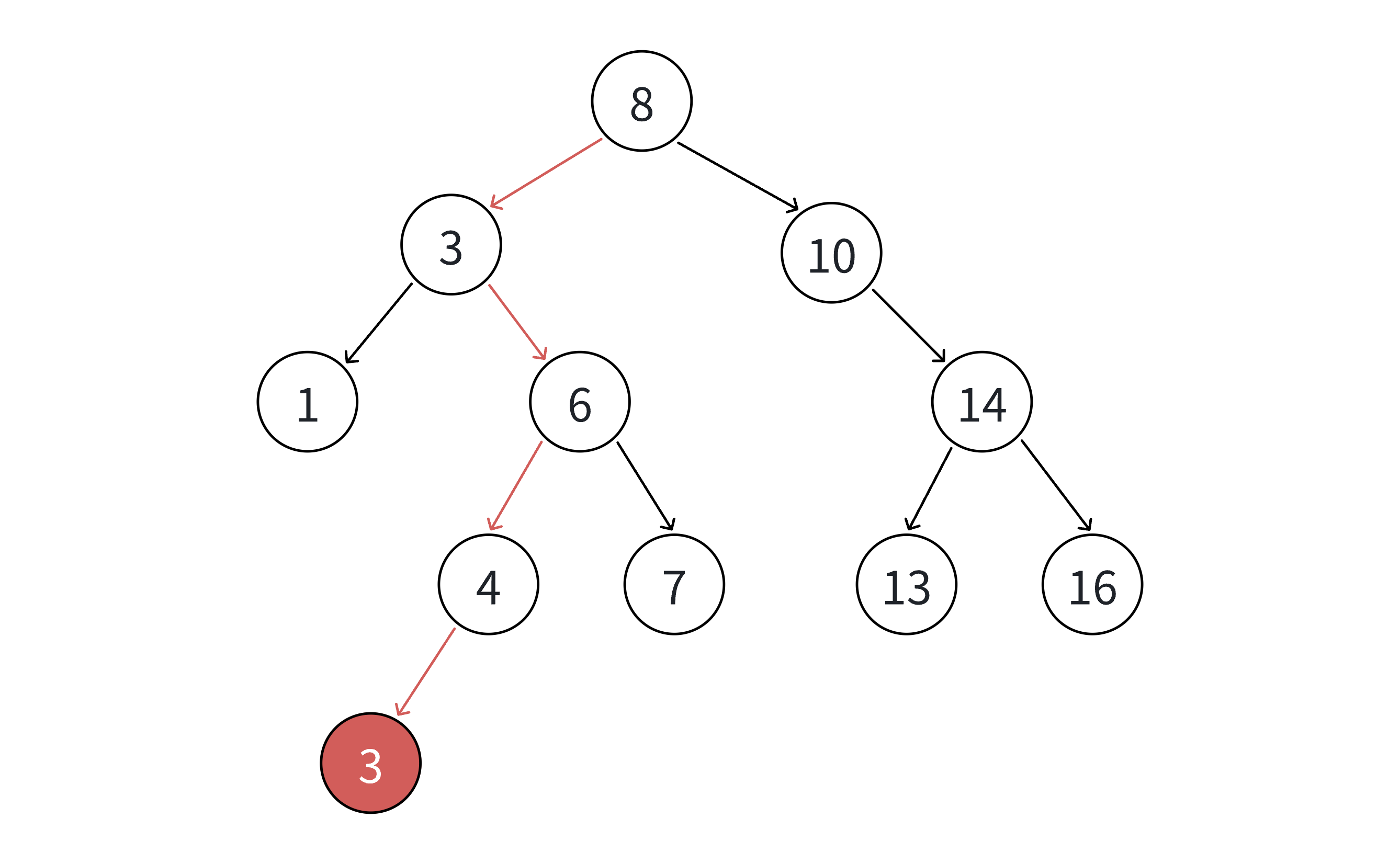
插⼊的具体过程如下:
树为空,则直接新增结点,赋值给root指针
树不空,按⼆叉搜索树性质,插⼊值⽐当前结点⼤往右⾛,插⼊值⽐当前结点⼩往左⾛,找到空位
置,插⼊新结点。如果⽀持插⼊相等的值,插⼊值跟当前结点相等的值可以往右⾛,也可以往左⾛,找到空位置,插
⼊新结点。(要注意的是要保持逻辑⼀致性,插⼊相等的值不要⼀会往右⾛,⼀会往左⾛)
⼆叉搜索树的删除
⾸先查找元素是否在⼆叉搜索树中,如果不存在,则返回false。
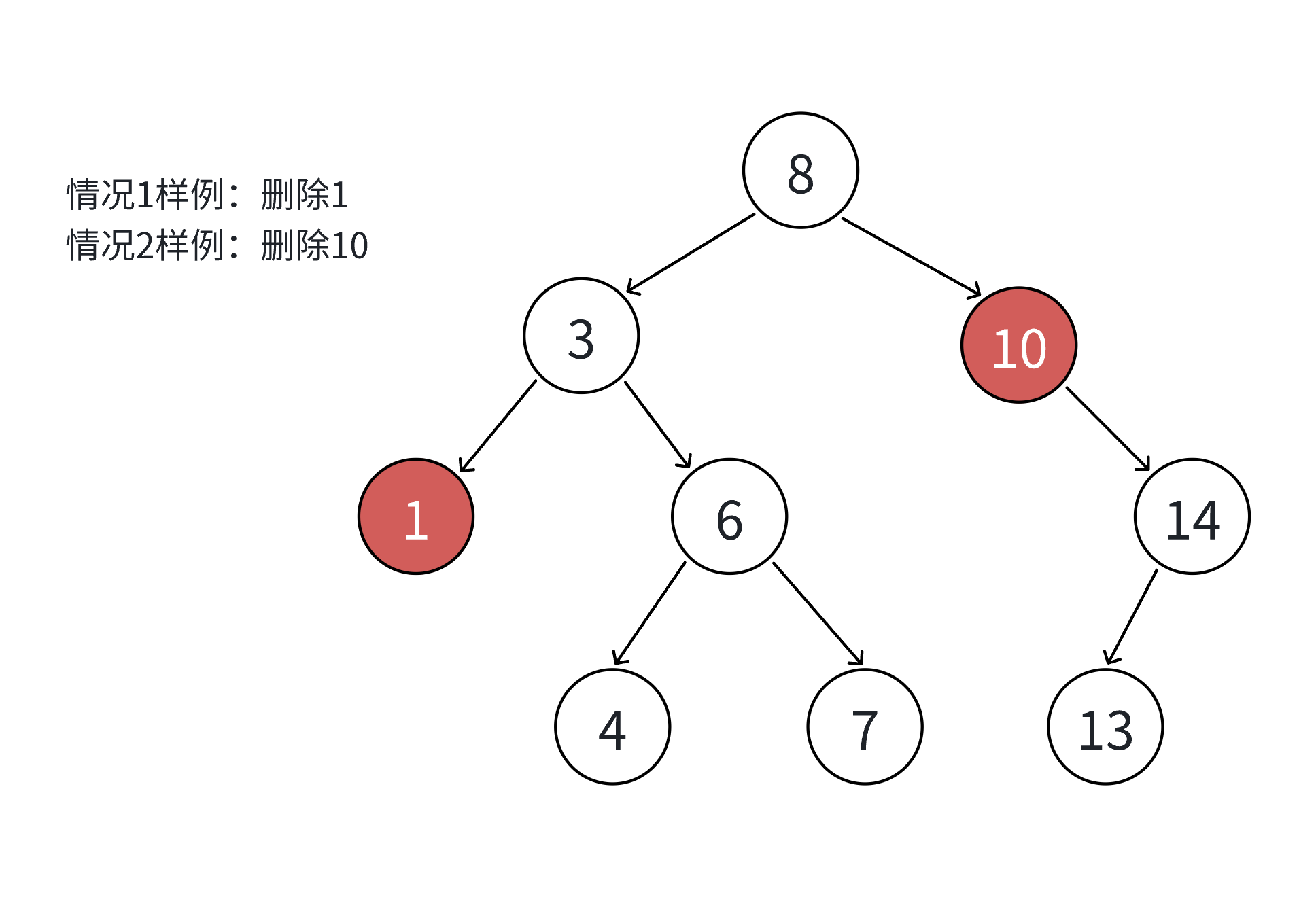
如果查找元素存在则分以下四种情况分别处理:(假设要删除的结点为N)
要删除结点N左右孩⼦均为空
要删除的结点N左孩⼦位空,右孩⼦结点不为空
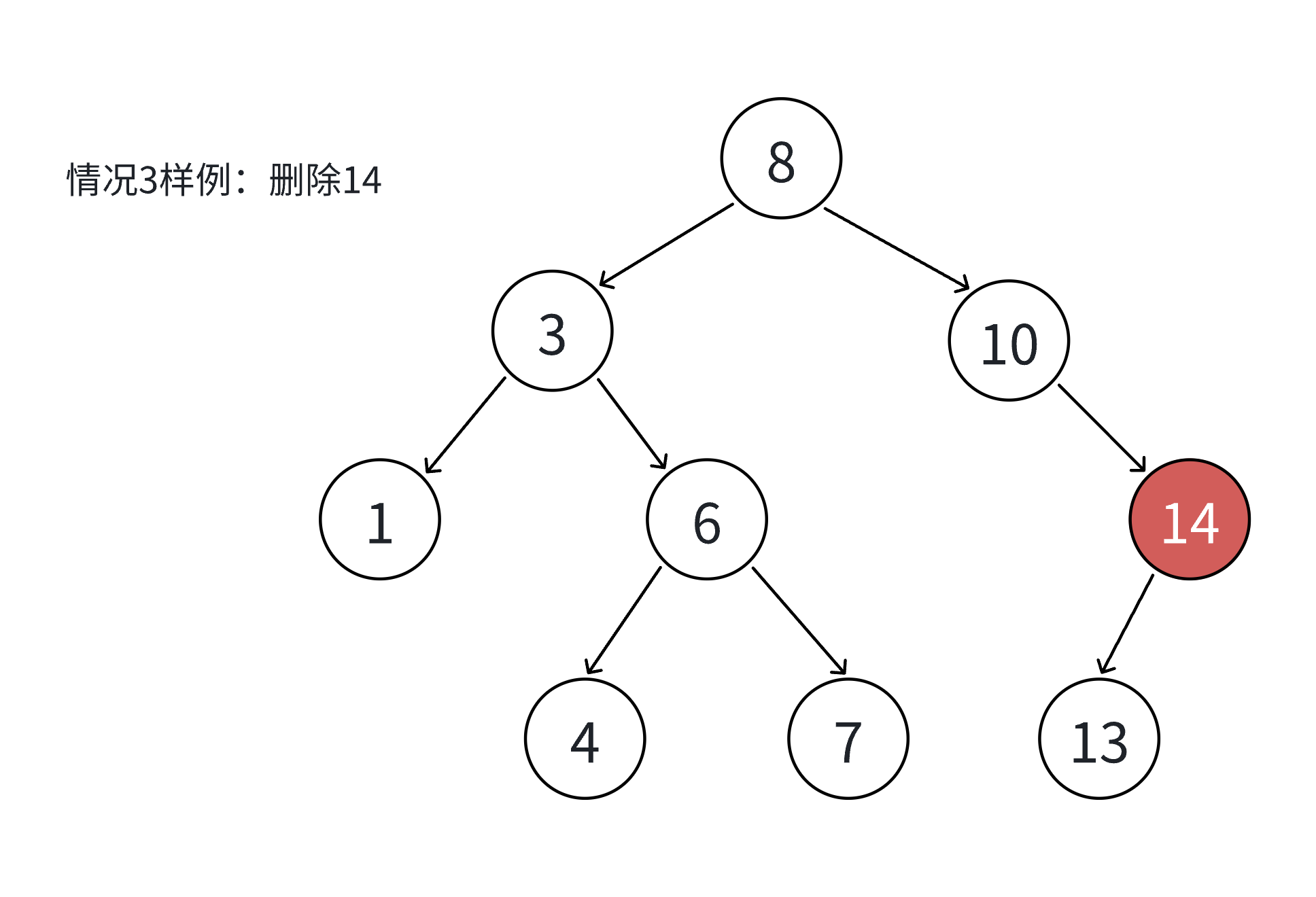
要删除的结点N右孩⼦位空,左孩⼦结点不为空
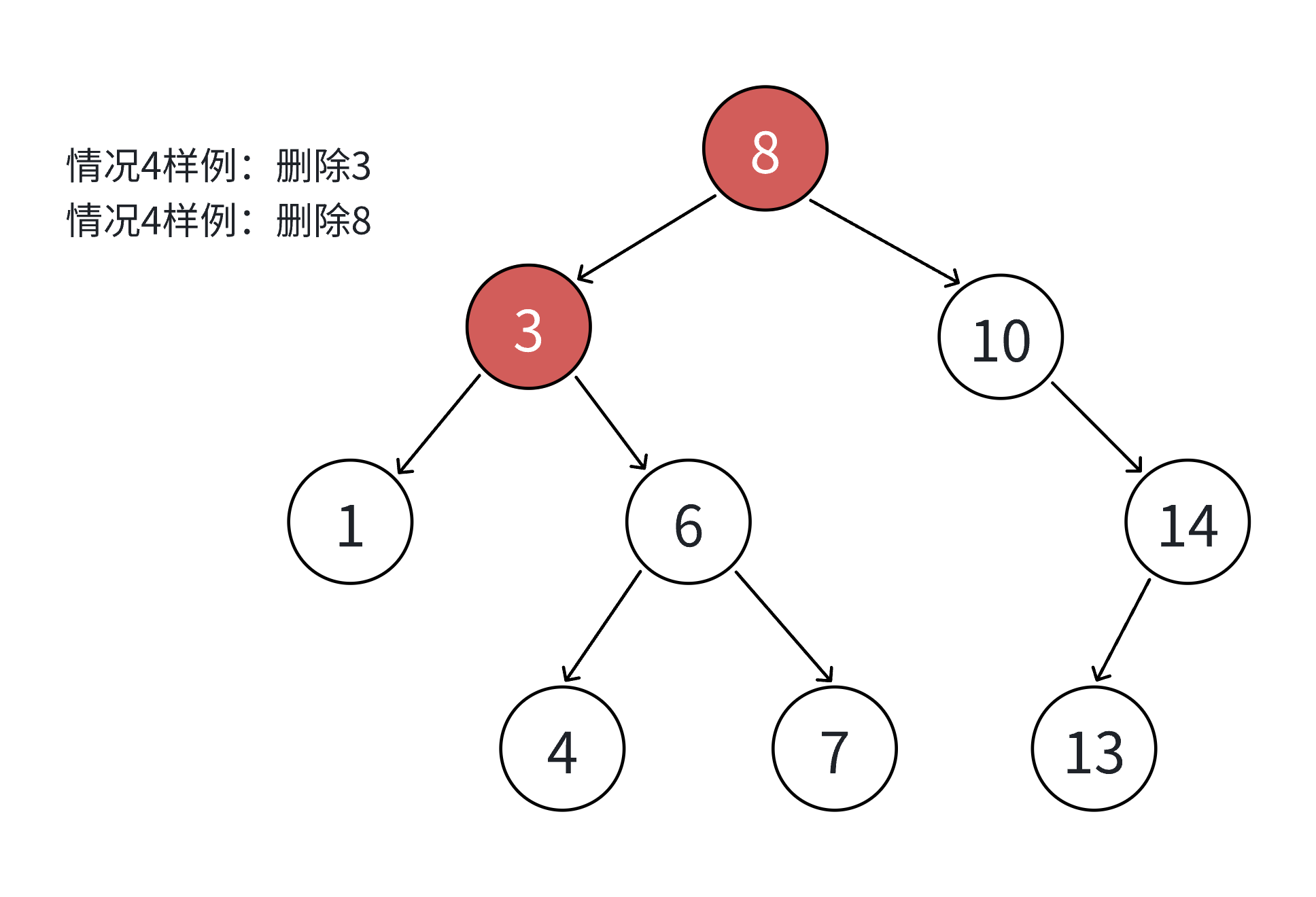
要删除的结点N左右孩⼦结点均不为空
对应以上四种情况的解决⽅案:把N结点的⽗亲对应孩⼦指针指向空,直接删除N结点(情况1可以当成2或者3处理,效果是⼀样
的)把N结点的⽗亲对应孩⼦指针指向N的右孩⼦,直接删除N结点
把N结点的⽗亲对应孩⼦指针指向N的左孩⼦,直接删除N结点
⽆法直接删除N结点,因为N的两个孩⼦⽆处安放,只能⽤替换法删除。找N左⼦树的值最⼤结点
R(最右结点)或者N右⼦树的值最⼩结点R(最左结点)替代N,因为这两个结点中任意⼀个,放到N的
位置,都满⾜⼆叉搜索树的规则。替代N的意思就是N和R的两个结点的值交换,转⽽变成删除R结
点,R结点符合情况2或情况3,可以直接删除。
❀三、 二叉搜索树代码实现
1.1二叉树定义
//-----------------------------------------------------------------------------------------
//1.1二叉树结构定义
/*
typedef 不支持模板化 1.2
template<class T>
typedef struct tree
{
second_tree* font;
second_tree* end;
T x;
}tr;
*/
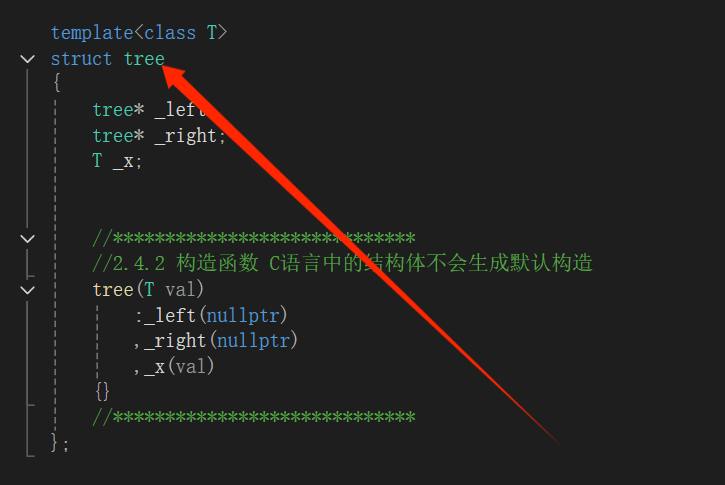
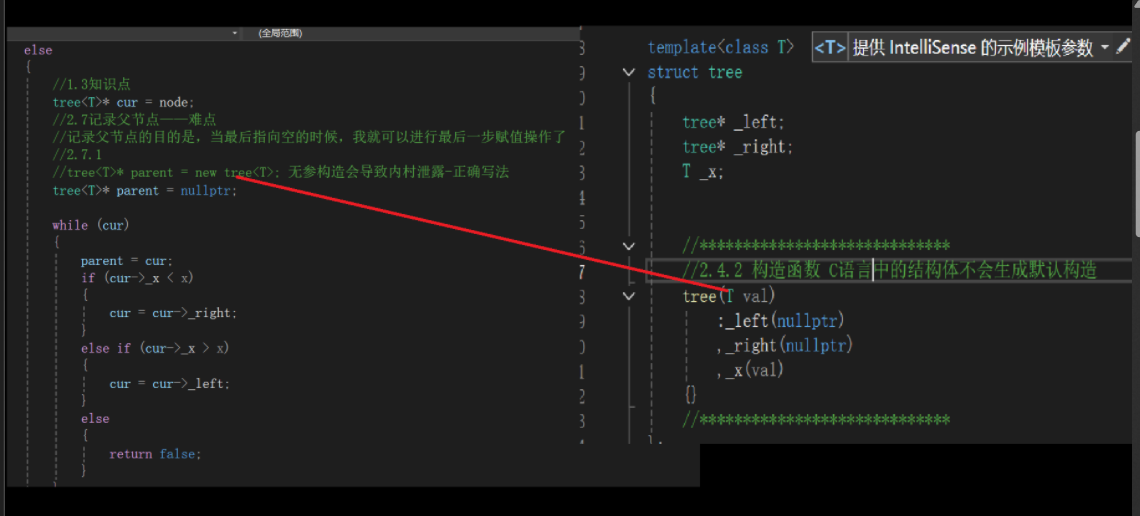
template<class T>
struct tree
{
tree* _left;
tree* _right;
T _x;
//*****************************
//2.4.2 构造函数 C语言中的结构体不会生成默认构造
tree(T val)
:_left(nullptr)
,_right(nullptr)
,_x(val)
{}
//*****************************
};template<class T>
class Tree
{
public:
private:
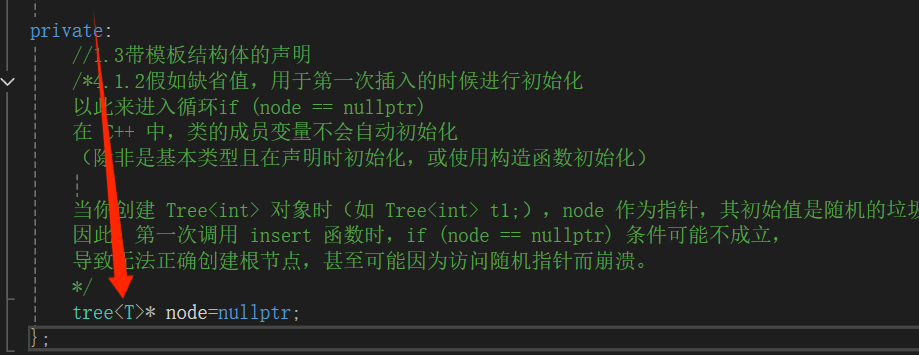
//1.3带模板结构体的声明
tree<T>* node=nullptr;
};1.1typedef 不支持模板化 不可以和template<class T 联用
>
这里 T x 会报错
1.2.C语言中的结构题可以用在cpp中类中,这样后续函结构体名书写会很方便
2.insert插入
public:
//*****************************
//2.1插入函数构造
//2.2返回值是bool型,参数类型是T类型
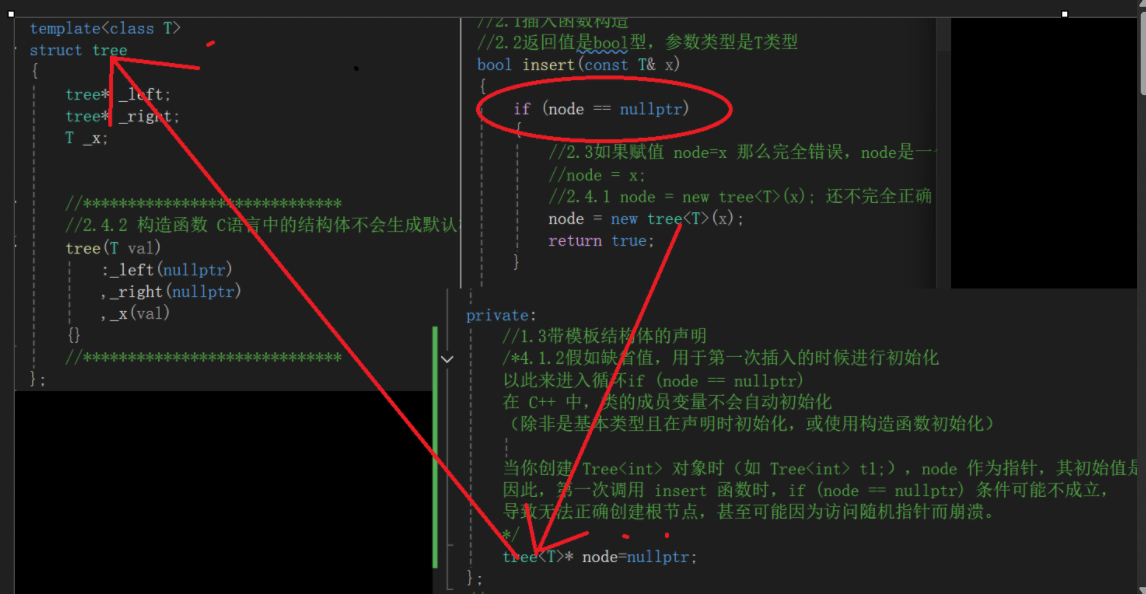
bool insert(const T& x)
{
if (node == nullptr)
{
//2.3如果赋值 node=x 那么完全错误,node是一个结构体指针型,node=x接受的是int型
//node = x;
//2.4.1 node = new tree<T>(x); 还不完全正确 还需要在原结构体进行初始化,
node = new tree<T>(x);
return true;
}
//2.6如果不为空
else
{
//1.3知识点
tree<T>* cur = node;
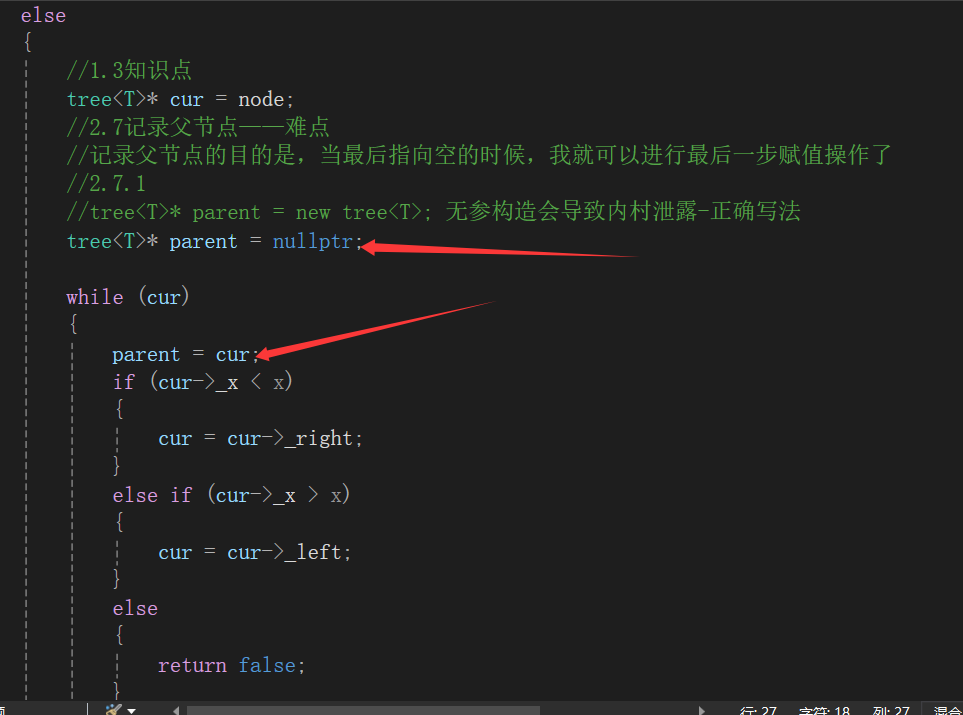
//2.7记录父节点——难点
//记录父节点的目的是,当最后指向空的时候,我就可以进行最后一步赋值操作了
//2.7.1
//tree<T>* parent = new tree<T>; 无参构造会导致内村泄露-正确写法
tree<T>* parent = nullptr;
while (cur)
{
parent = cur;
if (cur->_x < x)
{
cur = cur->_right;
}
else if (cur->_x > x)
{
cur = cur->_left;
}
else
{
return false;
}
}
//2.8进行最后的插入
if (parent->_x < x)
{
//最后的插入 创造新节点 付给大树
parent->_right = new tree<T>(x);
}
else
{
parent->_left = new tree<T>(x);
}
return true;
}
}2.1插入函数返回类型为bool型,若成功则返回true,失败则返回false
2.2node赋值类型
根据Tree类中的私有函数的声明可以确定->node为 tree T* 类型 而且是一个指针
因此只能声明node = new tree int()
2.3.初始化问题,struct里面构造函数的实现
node创建的是结构体 tree类,结构体是C语言语法,当第一次创建node时,里面为随机值——垃圾之。会导致不会进入if循环。
2.4无参构造导致内存泄露
这里已经明确了,tree构建一定要传进去一个参数,否则就会导致无参构造。无参构造那么就会导致内存泄露。
2.5记录父节点和插入的操作
3.print打印
//*****************************
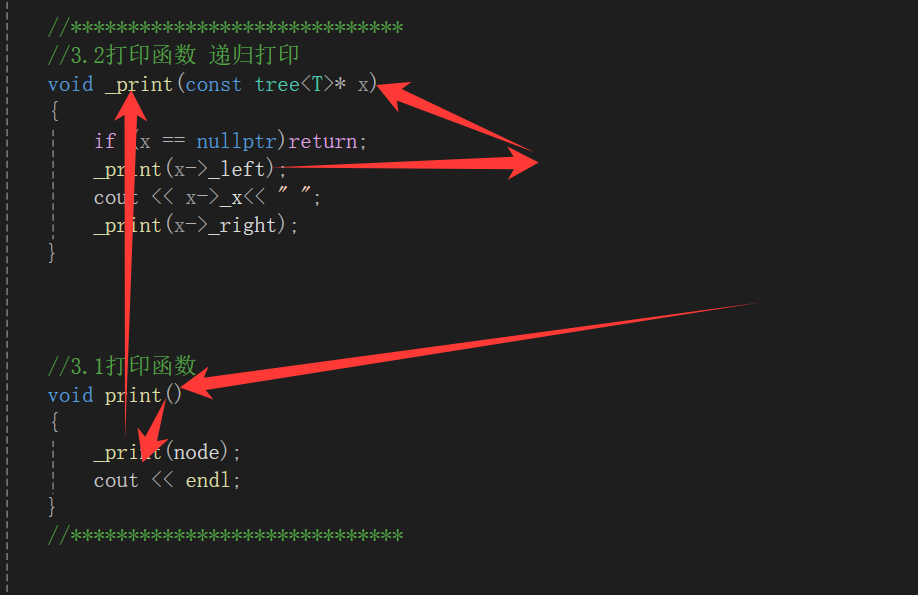
//3.2打印函数 递归打印
void _print(const tree<T>* x)
{
if (x == nullptr)return;
_print(x->_left);
cout << x->_x<< " ";
_print(x->_right);
}
//3.1打印函数
void print()
{
_print(node);
cout << endl;
}核心思维:递归
4.实例化
#include"tree.h"
int main()
{
//4.1实例化插入
int arr[] = { 1,5,9,6,3,2,8,7,4 };
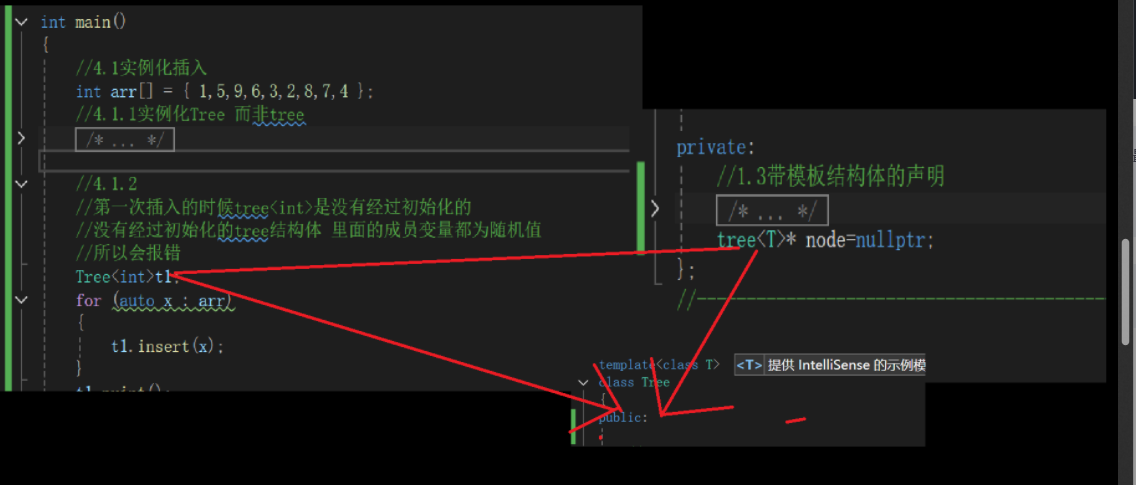
//4.1.1实例化Tree 而非tree
/*
tree<int>
1.这是一个模板结构体它内部包含:
数据成员:_left(左孩子指针)、
_right(右孩子指针)、
_x(节点值)。
构造函数:tree(T val) 用于初始化一个节点。
Tree<int>
2.这是一个模板类它内部包含:
成员变量:node(指向根节点的指针,类型为 tree<T>*)。
成员函数:insert(插入节点)、print(打印树)等,用于操作整棵树。
总结:
tree<T>:二叉树的节点结构,需要带参数构造,仅表示单个节点。
Tree<T>:二叉树的管理类,封装了树的整体操作,实例化后代表一棵完整的树。
tree<int> 报错的原因:缺少默认构造函数,无法无参实例化(但它本就不是用来表示 “树” 的)。
*/
//4.1.2
//第一次插入的时候tree<int>是没有经过初始化的
//没有经过初始化的tree结构体 里面的成员变量都为随机值
//所以会报错
Tree<int>t1;
for (auto x : arr)
{
t1.insert(x);
}
t1.print();
t1.erase(5);
t1.print();
t1.erase(0);
t1.print();
return 0;
}4.1涉及实例化 哪个大就实例化哪个。对于类和struct,类是一个完整功能的封装,二struct仅仅是对最底层的封装。因此类>struct,因此实例化类
涉及节点 哪个小就封装哪个,struct<类 因此创建struct
4.2类初始化问题——缺省参数
在实例化创建类的过程、对于自定义成员需要调用它的默认构造。而node默认构造里面是没有进行初始化值的解决。因此我们要加上缺省参数。否则就会报错。
5.删除
//5.1删除
bool erase(const T& x)
{
//5.1.1这里需要实例化tree<T>而不是node<T>
/*
node 是成员变量,不是类型:node 是 Tree 类中的成员变量(类型为 tree<T>*),
不是一个类型名,因此无法用 node<int> 来实例化指针。
是模板结构体 tree<T> 实例化后的类型(T=int),
表示存储 int 类型的二叉树节点,是一个合法的类型。
例如:tree<int>* node = new tree<int>(10); // 正确:定义一个存储int的节点指针
node 是 Tree 类中的成员变量(类型为 tree<T>*),不是类型名。
因此 node<int> 是语法错误—— 你试图将成员变量当作类型来实例化,这在 C++ 中不被允许。
*/
tree<T>* parent = nullptr;
tree<T>* cur = node;
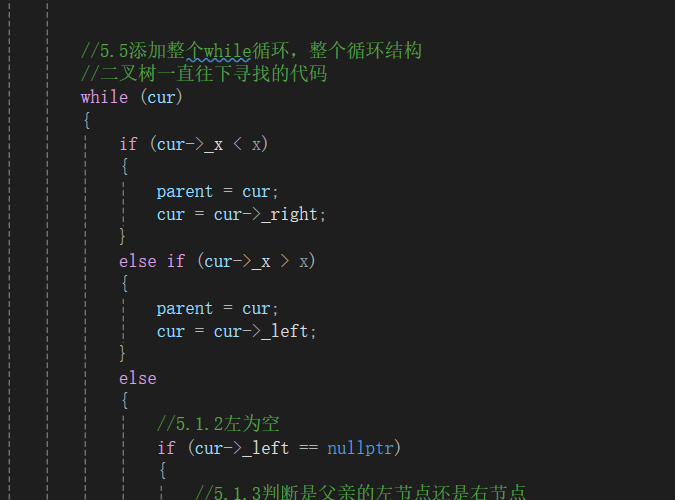
//5.5添加整个while循环,整个循环结构
//二叉树一直往下寻找的代码
while (cur)
{
if (cur->_x < x)
{
parent = cur;
cur = cur->_right;
}
else if (cur->_x > x)
{
parent = cur;
cur = cur->_left;
}
else
{
//5.1.2左为空
if (cur->_left == nullptr)
{
//5.1.3判断是父亲的左节点还是右节点
if (cur == parent->_left)
{
//5.1.4赋值parent
parent->_left = cur->_right;
}
else
{
parent->_right = cur->_right;
}
}
else if (cur->_right == nullptr)
{
if (cur == parent->_left)
{
parent->_left = cur->_left;
}
else
{
parent->_right = cur->_left;
}
}
//5.2左右均不为空
else
{
//5.2.1这里采用找右子树的最小节点
tree<T>* tmp = cur->_right;
//5.3创建被删除的父亲
tree<T>* tmpP = nullptr;
//5.2.2判断左子树是否为空
while (tmp->_left)
{
//5.3重难点理解
//删除之后 我们就破坏了原有的二叉树结构,
//被删除的位置,其父亲,需要重新连接被删除位置它的儿子
tmpP = tmp;
tmp = tmp->_left;
}
//5.2.3被删除的值==整个右子树中的最小值
cur->_x = tmp->_x;
//5.4特殊情况判断,当根节点的第一个右子树就是被删除的
if (tmpP->_left == tmp)
{
tmpP->_left = tmp->_right;
}
else
{
tmpP->_right = tmp->_right;
}
delete tmp;
return true;
}
}
}
return false;
}删除着重讲方法,以及需要注意事项。需要自己手动多敲代码来实现
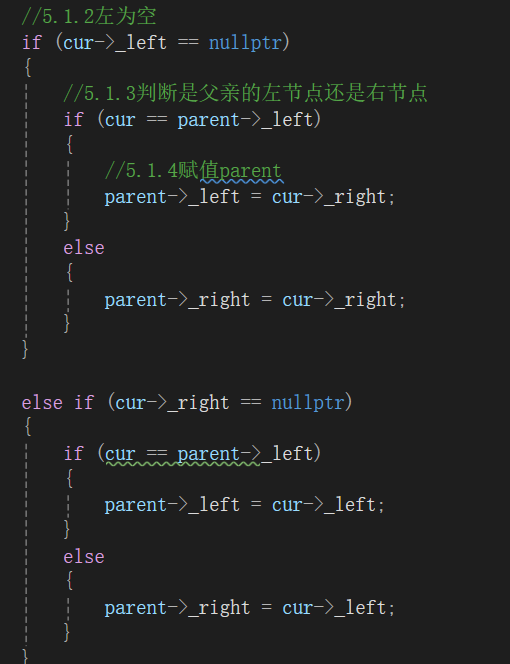
5.1左为空或者右为空
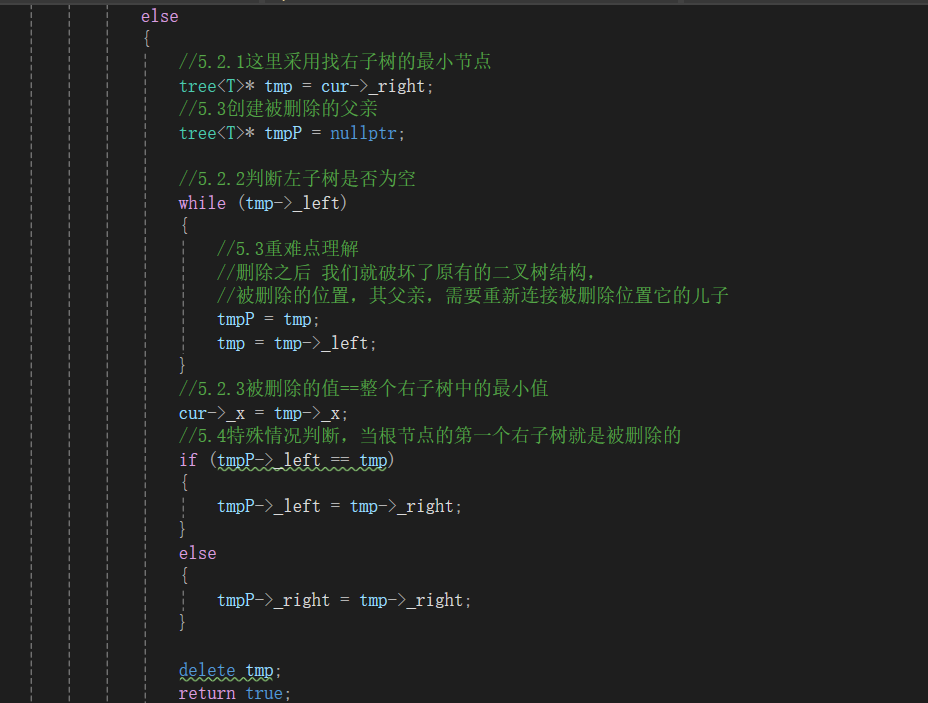
5.2左右均不为空
以下三个图分别为 初阶-> 补充 -> 最终形态
分两步
1.是补充父亲节点即5.3重难点理解
2.是特殊情况的判断即5.4特殊情况的判断
四、key和 key/value关键字
7.1 key搜索场景:
只有key作为关键码,结构中只需要存储key即可,关键码即为需要搜索到的值,搜索场景只需要判断key在不在。key的搜索场景实现的⼆叉树搜索树⽀持增删查,但是不⽀持修改,修改key破坏搜索树结构了。
场景1:⼩区⽆⼈值守⻋库,⼩区⻋库买了⻋位的业主⻋才能进⼩区,那么物业会把买了⻋位的业主的⻋牌号录⼊后台系统,⻋辆进⼊时扫描⻋牌在不在系统中,在则抬杆,不在则提⽰⾮本⼩区⻋辆,⽆法进⼊。
场景2:检查⼀篇英⽂ 章单词拼写是否正确,将词库中所有单词放⼊⼆叉搜索树,读取⽂章中的单词,查找是否在⼆叉搜索树中,不在则波浪线标红提⽰。
key/value搜索场景:
每⼀个关键码key,都有与之对应的值value,value可以任意类型对象。树的结构中(结点)除了需要存
储key还要存储对应的value,增/删/查还是以key为关键字⾛⼆叉搜索树的规则进⾏⽐较,可以快速查找到key对应的value。key/value的搜索场景实现的⼆叉树搜索树⽀持修改,但是不⽀持修改key,修改key破坏搜索树性质了,可以修改value。
场景1:简单中英互译字典,树的结构中(结点)存储key(英⽂)和vlaue(中⽂),搜索时输⼊英⽂,则同时
查找到了英⽂对应的中⽂。
场景2:商场⽆⼈值守⻋库,⼊⼝进场时扫描⻋牌,记录⻋牌和⼊场时间,出⼝离场时,扫描⻋牌,查
找⼊场时间,⽤当前时间-⼊场时间计算出停⻋时⻓,计算出停⻋费⽤,缴费后抬杆,⻋辆离场。
场景3:统计⼀篇⽂章中单词出现的次数,读取⼀个单词,查找单词是否存在,不存在这个说明第⼀次
出现,(单词,1),单词存在,则++单词对应的次数。
代码实现
主要区别和功能
#include<string>
#include<iostream>
using namespace std;
template<class K, class V>
struct BSTNode
{
K _key;
V _value;
BSTNode<K, V>* _left;
BSTNode<K, V>* _right;
BSTNode(const K& key, const V& value)
:_key(key)
, _value(value)
, _left(nullptr)
, _right(nullptr)
{}
};
template<class K, class V>
class BSTree
{
typedef BSTNode<K, V> Node;
public:
BSTree() = default;
BSTree(const BSTree<K, V>& t)
{
_root = Copy(t._root);
}
BSTree<K, V>& operator=(BSTree<K, V> t)
{
swap(_root, t._root);
return *this;
}
~BSTree()
{
Destroy(_root);
_root = nullptr;
}
bool Insert(const K& key, const V& value)
{
if (_root == nullptr)
{
_root = new Node(key, value);
return true;
}
Node* parent = nullptr;
Node* cur = _root;
while (cur)
{
if (cur->_key < key)
{
parent = cur;
cur = cur->_right;
}
else if (cur->_key > key)
{
parent = cur;
cur = cur->_left;
}
else
{
return false;
}
}
cur = new Node(key, value);
if (parent->_key < key)
{
parent->_right = cur;
}
else
{
parent->_left = cur;
}
return true;
}
Node* Find(const K& key)
{
Node* cur = _root;
while (cur)
{
if (cur->_key < key)
{
cur = cur->_right;
}
else if (cur->_key > key)
{
cur = cur->_left;
}
else
{
return cur;
}
}
return nullptr;
}
bool Erase(const K& key)
{
Node* parent = nullptr;
Node* cur = _root;
while (cur)
{
if (cur->_key < key)
{
parent = cur;
cur = cur->_right;
}
else if (cur->_key > key)
{
parent = cur;
cur = cur->_left;
}
else
{
if (cur->_left == nullptr)
{
if (parent == nullptr)
{
_root = cur->_right;
}
else
{
if (parent->_left == cur)
parent->_left = cur->_right;
else
parent->_right = cur->_right;
}
delete cur;
return true;
}
else if (cur->_right == nullptr)
{
if (parent == nullptr)
{
_root = cur->_left;
}
else
{
if (parent->_left == cur)
parent->_left = cur->_left;
else
parent->_right = cur->_left;
}
delete cur;
return true;
}
else
{
Node* rightMinP = cur;
Node* rightMin = cur->_right;
while (rightMin->_left)
{
rightMinP = rightMin;
rightMin = rightMin->_left;
}
cur->_key = rightMin->_key;
if (rightMinP->_left == rightMin)
rightMinP->_left = rightMin->_right;
else
rightMinP->_right = rightMin->_right;
delete rightMin;
return true;
}
}
}
return false;
}
void InOrder()
{
_InOrder(_root);
cout << endl;
}
private:
void _InOrder(Node* root)
{
if (root == nullptr)
{
return;
}
_InOrder(root->_left);
cout << root->_key << ":" << root->_value << endl;
_InOrder(root->_right);
}
void Destroy(Node* root)
{
if (root == nullptr)
return;
Destroy(root->_left);
Destroy(root->_right);
delete root;
}
Node* Copy(Node* root)
{
if (root == nullptr)
return nullptr;
Node* newRoot = new Node(root->_key, root->_value);
newRoot->_left = Copy(root->_left);
newRoot->_right = Copy(root->_right);
return newRoot;
}
private:
Node* _root = nullptr;
};
// 词典功能测试
void TestDict()
{
BSTree<string, string> dict;
dict.Insert("left", "左边");
dict.Insert("right", "右边");
dict.Insert("insert", "插入");
dict.Insert("string", "字符串");
string str;
while (cin >> str)
{
auto ret = dict.Find(str);
if (ret)
{
cout << "->" << ret->_value << endl;
}
else
{
cout << "无此单词,请重新输入" << endl;
}
}
}
// 水果计数功能测试
void TestCount()
{
string arr[] = { "苹果", "西瓜", "苹果", "西瓜", "苹果", "苹果", "西瓜", "苹果", "香蕉", "苹果", "香蕉" };
BSTree<string, int> countTree;
for (const auto& str : arr)
{
auto ret = countTree.Find(str);
if (ret == nullptr)
{
countTree.Insert(str, 1);
}
else
{
ret->_value++;
}
}
countTree.InOrder();
}
int main()
{
// 选择测试功能,取消注释其中一个即可
// TestDict();
TestCount();
return 0;
}








 浙公网安备 33010602011771号
浙公网安备 33010602011771号