【高阶数据结构】红黑树 - 教程
目录
1. 什么是红黑树
红黑树并不是一个完全平衡的二叉树(像AVL树那样),而是一种近似平衡的二叉搜索树。它通过一套简单的规则和调整操作,确保树的高度始终维持在 O(log n) 级别,从而保证了搜索、插入、删除等操作的高效性。
二叉树高度:[log n,n-1]
平衡二叉树 / AVL 树、 红黑树高度:O(log n)
它通过以下5条规则来维持这种平衡:
- 每个节点不是红色就是黑色。
- 根节点是黑色的。
- 如果一个节点是红色的,则它的两个子节点都是黑色的。(即:不能有连续的红色节点)
- 对于每个节点,从该节点到其所有后代叶节点的简单路径上,均包含相同数目的黑色节点。
- 每个叶子节点(NIL节点,空节点)都是黑色的。(此规则在实现中通常作为隐含条件)
规则3和规则4是重中之重,插入操作的所有调整都是为了维护这两条规则。
其实可以看出,这5条规则导致:红黑树最长路径最多是最短路径的两倍。
2. 红黑树的模拟实现
2.1 插入
插入操作的整体思路:
插入新节点时,我们遵循一个核心原则:先按二叉搜索树规则插入,再通过调整来恢复红黑树性质。
为什么新插入的节点默认为红色?
- 如果插入黑色节点,会立即违反规则4,因为它所在路径的黑色节点数会增加1,修复起来非常困难,需要调整整棵树。
- 如果插入红色节点,可能违反规则3(如果父节点也是红色),但不会违反规则4。违反规则3是一个局部问题,更容易通过局部调整来修复。
因此,插入过程可以简化为:解决因插入红色节点而导致的“双红”问题。
这一段其实和AVL树的插入一样。
bool Insert(const pair<K, V>& kv)
{
if (_root == nullptr)
{
_root = new Node(kv);
_root->_col = BLACK;
return true;
}
else
{
Node* parent = nullptr;
Node* cur = _root;
//找到节点所处的位置
while (cur)
{
if (kv.first > cur->_kv.first)
{
parent = cur;
cur = cur->_right;
}
else if (kv.first < cur->_kv.first)
{
parent = cur;
cur = cur->_left;
}
else
{
return false;
}
}
//生成节点
cur = new Node(kv);
cur->_col = RED;
//连接节点
cur->_parent = parent;
if (cur->_kv.first > parent->_kv.first)
{
parent->_right = cur;
}
else
{
parent->_left = cur;
}
//通过调整来恢复红黑树性质
//...
}
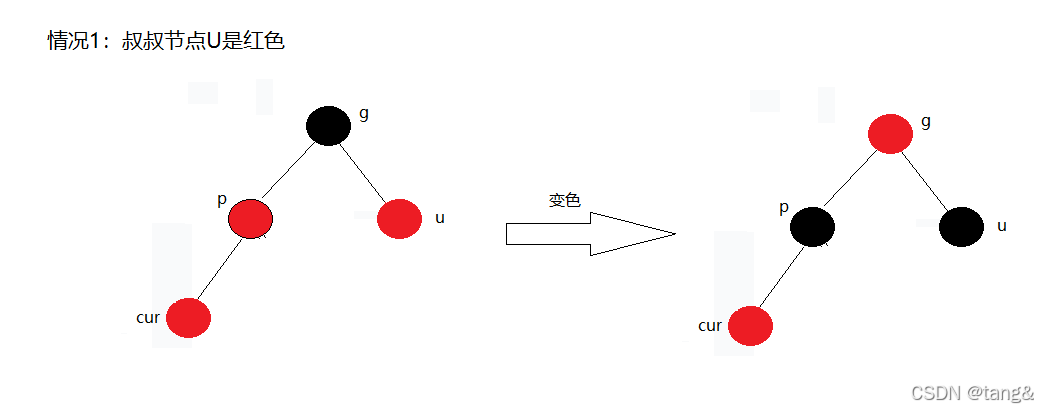
}2.1.1 情况1:叔叔节点U是红色
这是最简单的情况。
处理策略:重新着色
操作步骤:
- 将父节点P和叔叔节点U都变为黑色。
- 将祖父节点G变为红色。
- 把祖父节点G当作新的当前节点C,继续向上检查。
为什么这样做?
- 步骤1解决了P和C之间的“双红”问题。
- 步骤2保证了以G为根的子树黑色高度不变(因为黑色节点只是从P和U转移到了G)。
- 步骤3是因为G现在变成了红色,如果G的父节点也是红色,就会产生新的“双红”问题,需要继续向上处理。如果调整后,最顶部的节点是黑色,则不用向上处理,插入结束(接下来的情况二就是这样)。
特殊情况:如果G是根节点,在最后需要将其重新变为黑色(规则2)。
注意:只有是出现双红的情况,祖父节点G一定是黑色,因为P是红色。
2.1.2 情况2:叔叔节点U是黑色或为空(NIL)
这种情况需要旋转来解决。旋转的目的是为了提升C节点,同时保持二叉搜索树的性质。
情况2又分为两个子情况,取决于当前节点C是父节点P的左孩子还是右孩子。
(1)情况2a:直线型 (LL / RR)
- LL型:P是G的左孩子,C是P的左孩子。
- RR型:P是G的右孩子,C是P的右孩子。
处理策略:一次旋转 + 重新着色
操作步骤(以LL型为例):
- 对祖父节点G进行一次右旋。
- 重新着色:将原来的父节点P变为黑色,原来的祖父节点G变为红色。
- 调整结束,无需继续向上(p为黑色)
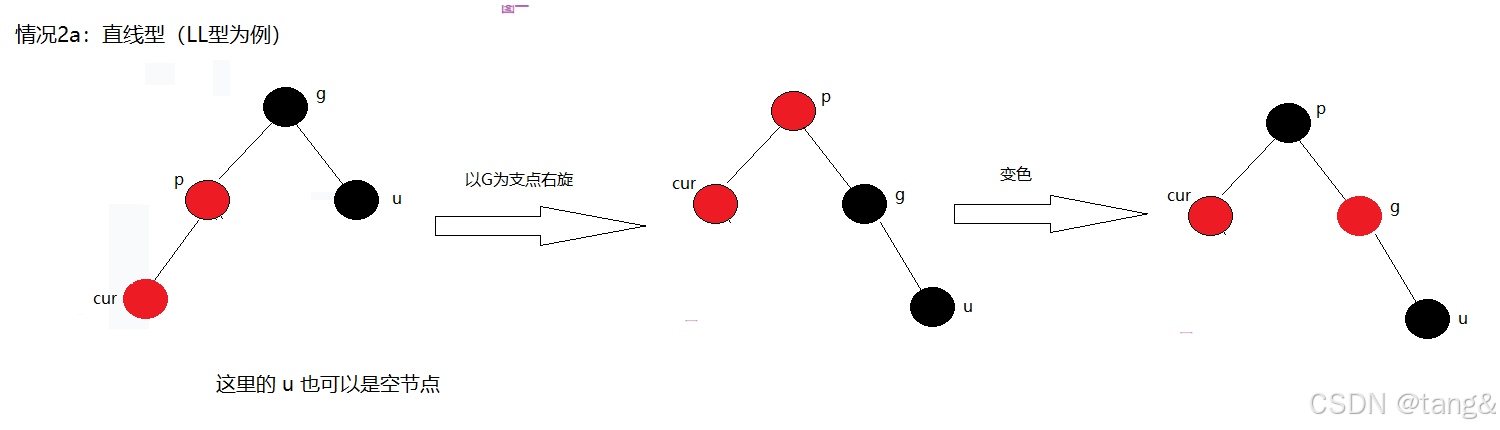
为什么这样做?
- 右旋使得P成为了新的局部根节点。
- 着色后,P(黑色)隔开了C(红色)和G(红色),彻底解决了“双红”问题。
- 旋转和着色后,该子树的黑色高度保持不变。
另附RR型示意图: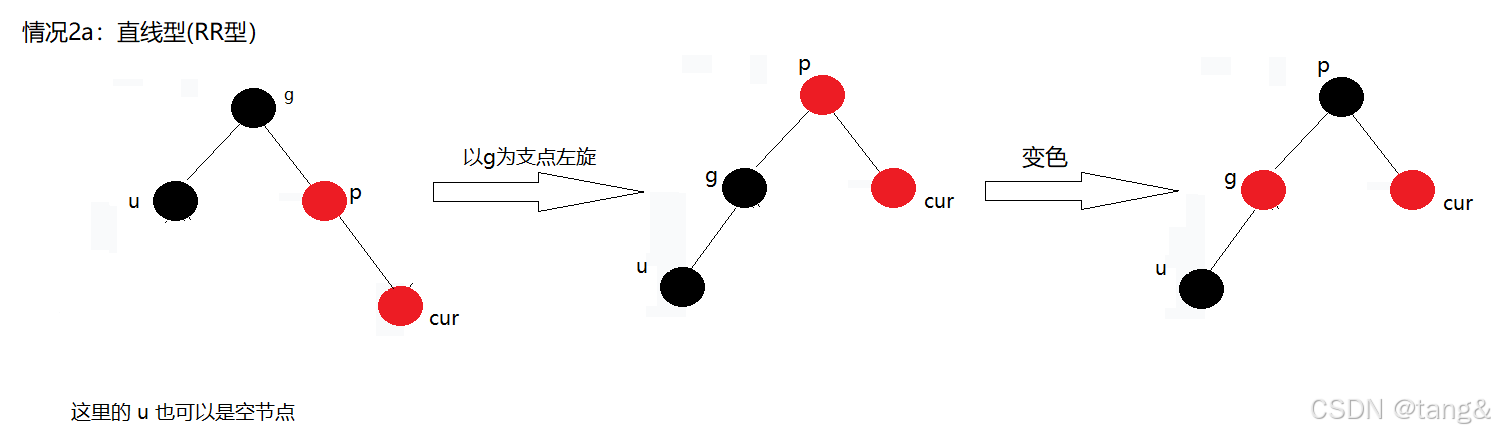
(2)情况2b:折线型 (LR / RL)
- LR型:P是G的左孩子,C是P的右孩子。
- RL型:P是G的右孩子,C是P的左孩子。
处理策略:两次旋转 + 重新着色
操作步骤(以LR型为例):
- 对父节点P进行一次左旋。这一步将LR型转换成了LL型。
- 对祖父节点G进行一次右旋。
- 重新着色:将当前节点C变为黑色,原来的祖父节点G变为红色。
- 调整结束,无需继续向上(cur为黑色)
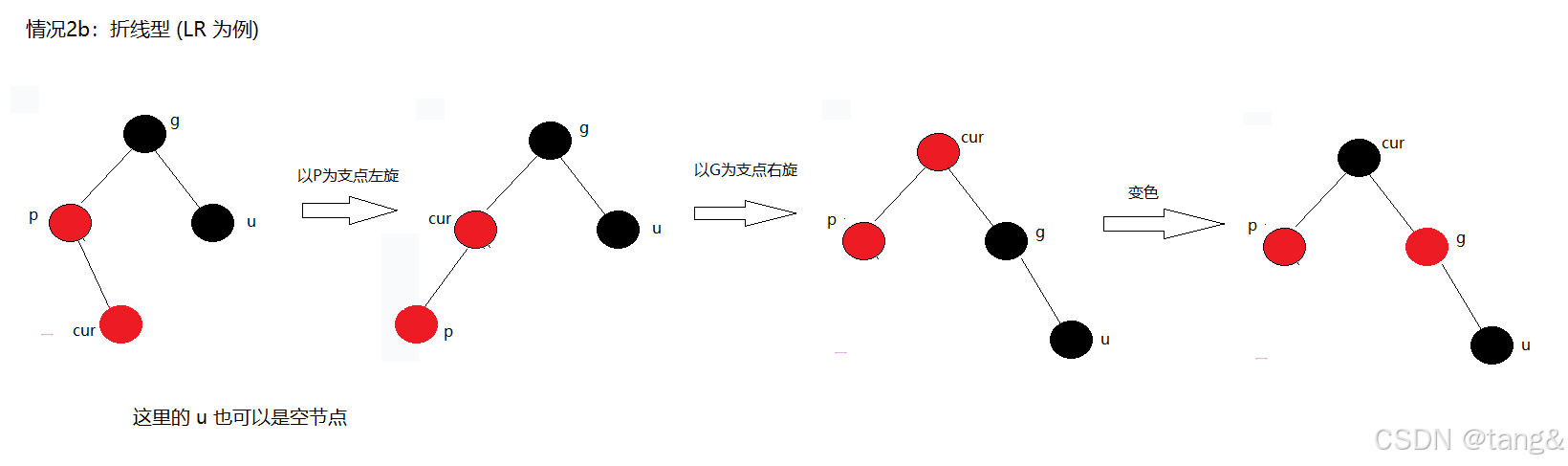
为什么这样做?
- 第一次旋转(左旋)将结构标准化。左旋后,其实已经就是情况2a了。
- 第二次旋转(右旋)将C提升到局部根节点的位置。
- 着色后,C(黑色)成为了新的局部根,隔开了两边的红色节点,彻底解决了问题。
另附RL型示意图: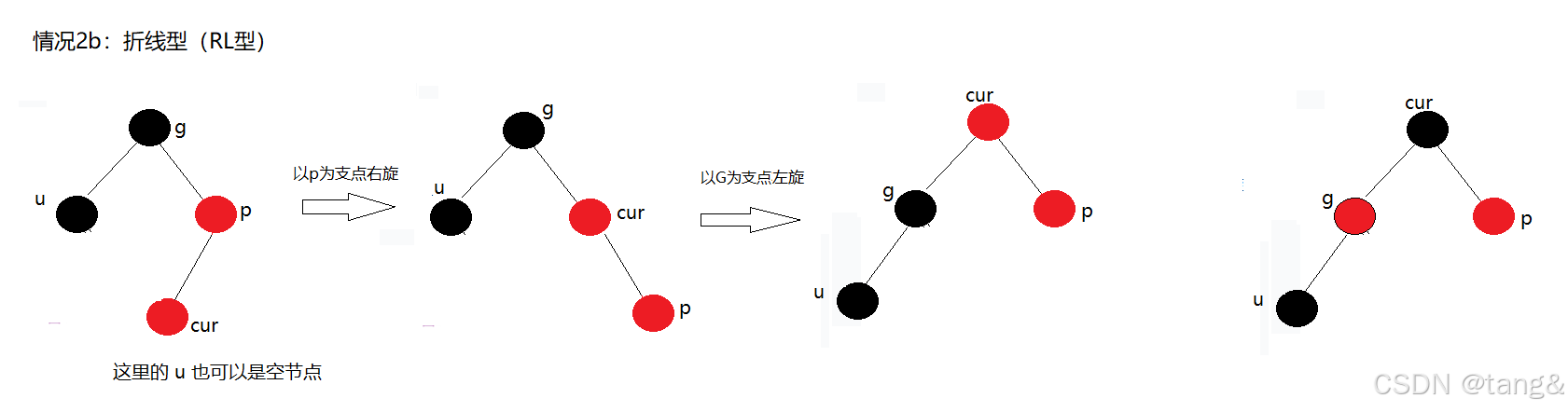
2.1.3 代码实现
左右单旋转的代码如下:
左右单旋转的详细讲解,可以看我的关于AVL树的博客:详细请点击<——
private:
void RotateL(Node* parent)
{
Node* ppnode = parent->_parent;
Node* cur = parent->_right;
Node* curleft = cur->_left;
parent->_right = curleft;
if (curleft)
{
curleft->_parent = parent;
}
cur->_left = parent;
parent->_parent = cur;
if (ppnode == nullptr)
{
_root = cur;
cur->_parent = nullptr;
}
else
{
cur->_parent = ppnode;
if (ppnode->_left == parent)
{
ppnode->_left = cur;
}
else
{
ppnode->_right = cur;
}
}
}
void RotateR(Node* parent)
{
Node* ppnode = parent->_parent;
Node* cur = parent->_left;
Node* curright = cur->_right;
parent->_left = curright;
if (curright)
{
curright->_parent = parent;
}
cur->_right = parent;
parent->_parent = cur;
if (ppnode == nullptr)
{
_root = cur;
cur->_parent = nullptr;
}
else
{
if (ppnode->_left == parent)
{
ppnode->_left = cur;
cur->_parent = ppnode;
}
else
{
ppnode->_right = cur;
cur->_parent = ppnode;
}
}
}红黑树插入的代码实现:
bool Insert(const pair<K, V>& kv)
{
if (_root == nullptr)
{
_root = new Node(kv);
_root->_col = BLACK;
return true;
}
else
{
Node* parent = nullptr;
Node* cur = _root;
while (cur)
{
if (kv.first > cur->_kv.first)
{
parent = cur;
cur = cur->_right;
}
else if (kv.first < cur->_kv.first)
{
parent = cur;
cur = cur->_left;
}
else
{
return false;
}
}
cur = new Node(kv);
cur->_col = RED;
cur->_parent = parent;
if (cur->_kv.first > parent->_kv.first)
{
parent->_right = cur;
}
else
{
parent->_left = cur;
}
while (parent && parent->_col == RED)//满足条件就不断向上调整
{
Node* grandfather = parent->_parent;
if (parent == grandfather->_left)//parent在grandfather的左边的情况
{
Node* uncle = grandfather->_right;//uncle叔叔节点对应在grandfather右边
if (uncle && uncle->_col == RED)//处理uncle存在且颜色为红色的情况
{
parent->_col = uncle->_col = BLACK;
grandfather->_col = RED;
cur = grandfather;
parent = cur->_parent;
_root->_col = BLACK;//保证红黑树的根节点始终为黑色
}
else//处理uncle不存在,或者uncle存在且颜色为黑色的情况
{
if (cur == parent->_left)
{
RotateR(grandfather);
parent->_col = BLACK;
grandfather->_col = RED;
}
else //cur = parent->_right
{
RotateL(parent);
RotateR(grandfather);
cur->_col = BLACK;
grandfather->_col = RED;
}
break;
}
}
else //parent == grandfather->_right//parent在grandfather的右边的情况
{
Node* uncle = grandfather->_left;//uncle叔叔节点对应在grandfather左边
if (uncle && uncle->_col == RED)//处理uncle存在且颜色为红色的情况
{
parent->_col = uncle->_col = BLACK;
grandfather->_col = RED;
cur = grandfather;
parent = cur->_parent;
_root->_col = BLACK;//保证红黑树的根节点始终为黑色
}
else//处理uncle不存在,或者uncle存在且颜色为黑色的情况
{
if (cur == parent->_right)
{
RotateL(grandfather);
parent->_col = BLACK;
grandfather->_col = RED;
}
else //cur = parent->_left
{
RotateR(parent);
RotateL(grandfather);
cur->_col = BLACK;
grandfather->_col = RED;
}
break;
}
}
}
return true;
}
}2.2 IsBalance
bool CheckColour(Node* root, int blacksum, int leftpathblack)
{
// 基准情况:到达叶子节点
if (root == nullptr) {
// 检查性质5:所有路径黑色节点数相同
if (blacksum != leftpathblack) {
cout << "每条路径上的黑色节点的数目不同" << endl;
return false;
}
return true;
}
Node* parent = root->_parent;
// 检查性质4:没有连续的红节点
if (parent && parent->_col == RED && root->_col == RED) {
cout << root->_kv.first << ':' << "出现两个连续的红节点" << endl;
return false;
}
// 统计当前路径的黑色节点数
if (root->_col == BLACK)
blacksum++;
// 递归检查左右子树
return CheckColour(root->_left, blacksum, leftpathblack) &&
CheckColour(root->_right, blacksum, leftpathblack);
}
bool IsBalance(Node* root)
{
if (root == nullptr) return true;
// 检查性质2:根节点必须是黑色
if (root->_col != BLACK) {
cout << "根节点颜色错误不为黑色" << endl;
return false;
}
// 计算最左路径的黑色节点数量作为基准
int leftpathblack = 0;
Node* cur = root;
while (cur) {
if (cur->_col == BLACK)
leftpathblack++;
cur = cur->_left;
}
return CheckColour(root, 0, leftpathblack);
}
bool IsBalance()
{
return IsBalance(_root);
}这段代码是用于检查红黑树是否平衡的函数实现。我来详细解释每个部分的功能:
整体结构
IsBalance(): 公开接口,调用内部实现。IsBalance(Node* root): 检查根节点和计算左路径黑色节点数。checkColour(): 递归检查红黑树性质。
函数详解
IsBalance(Node* root)
功能:
- 检查根节点是否为黑色(红黑树性质2)。
- 计算从根节点到最左叶子节点的黑色节点数量,作为基准值。
- 调用
checkColour进行递归检查。
CheckColour(Node* root, int blacksum, int leftpathblack)
功能:
- 性质4检查:确保没有连续的红节点。
- 性质5检查:确保所有路径的黑色节点数相同。
- 递归遍历整棵树。
检查的红黑树性质
- 性质2:根节点是黑色(在
IsBalance中检查)。 - 性质4:红色节点的子节点必须是黑色(在
CheckColour中检查)。 - 性质5:从任一节点到其每个叶子的所有路径都包含相同数目的黑色节点(在
CheckColour中检查)。
2.3 Height
int Height()
{
return Height(_root);
}
int Height(Node* root)
{
if (root == nullptr)
{
return 0;
}
int heightL = Height(root->_left);
int heightR = Height(root->_right);
return heightL > heightR ? heightL + 1 : heightR + 1;
}3. 红黑树与AVL树的对比
选择AVL树的场景:
- 查找频率远高于插入删除
- 数据相对有序或接近有序
- 涉及磁盘I/O等慢速存储
- I/O成本极高,减少查找次数是首要目标 → 选高度更低的AVL树
选择红黑树的场景:
- 频繁插入删除操作
- 数据随机分布
- 纯内存操作
- I/O成本可忽略,减少数据移动和缓存失效更重要 → 选旋转更少的红黑树
现实世界的例子:
适合AVL树的场景:
- 维基百科全文索引(构建一次,查询海量)
- 编译器符号表(构建相对少,查找频繁)
- 只读配置数据库
适合红黑树的场景:
- Linux进程调度(频繁插入删除进程)
- 数据库事务管理(频繁更新)
- 实时游戏状态管理
为啥有序的数的插入更适合AVL树?
根本原因:
- 调整策略不同
// AVL树:局部调整
if (平衡因子 > 1) {
旋转调整(); // 只影响局部子树
}
// 红黑树:可能传播调整
while (父节点是红色 && 违反规则) {
颜色变换();
if (仍然违反规则) {
旋转调整(); // 可能向上传播
}
}- 有序数据的特殊性
有序数据插入会形成"链式"结构,这正是:
- AVL树擅长处理的:通过单次旋转就能恢复平衡
- 红黑树不擅长的:需要复杂的颜色变换和可能的多次调整
4. 源代码
RBTree.h:
#pragma once
#include <iostream>
using namespace std;
enum Colour
{
RED,
BLACK
};
template<typename K, typename V>
struct RBTreeNode
{
pair<K, V> _kv;
RBTreeNode<K, V>* _left;
RBTreeNode<K, V>* _right;
RBTreeNode<K, V>* _parent;
Colour _col;
RBTreeNode(const pair<K, V> kv)
:_kv(kv)
,_left(nullptr)
,_right(nullptr)
,_parent(nullptr)
,_col(RED)
{}
};
template<typename K, typename V>
class RBTree
{
typedef RBTreeNode<K, V> Node;
public:
RBTree()
:_root(nullptr)
{}
bool Insert(const pair<K, V>& kv)
{
if (_root == nullptr)
{
_root = new Node(kv);
_root->_col = BLACK;
return true;
}
else
{
Node* parent = nullptr;
Node* cur = _root;
while (cur)
{
if (kv.first > cur->_kv.first)
{
parent = cur;
cur = cur->_right;
}
else if (kv.first < cur->_kv.first)
{
parent = cur;
cur = cur->_left;
}
else
{
return false;
}
}
cur = new Node(kv);
cur->_col = RED;
cur->_parent = parent;
if (cur->_kv.first > parent->_kv.first)
{
parent->_right = cur;
}
else
{
parent->_left = cur;
}
while (parent && parent->_col == RED)
{
Node* grandfather = parent->_parent;
if (parent == grandfather->_left)
{
Node* uncle = grandfather->_right;
if (uncle && uncle->_col == RED)
{
parent->_col = uncle->_col = BLACK;
grandfather->_col = RED;
cur = grandfather;
parent = cur->_parent;
_root->_col = BLACK;
}
else
{
if (cur == parent->_left)
{
RotateR(grandfather);
parent->_col = BLACK;
grandfather->_col = RED;
}
else //cur = parent->_right
{
RotateL(parent);
RotateR(grandfather);
cur->_col = BLACK;
grandfather->_col = RED;
}
break;
}
}
else //parent == grandfather->_right
{
Node* uncle = grandfather->_left;
if (uncle && uncle->_col == RED)
{
parent->_col = uncle->_col = BLACK;
grandfather->_col = RED;
cur = grandfather;
parent = cur->_parent;
_root->_col = BLACK;
}
else
{
if (cur == parent->_right)
{
RotateL(grandfather);
parent->_col = BLACK;
grandfather->_col = RED;
}
else //cur = parent->_left
{
RotateR(parent);
RotateL(grandfather);
cur->_col = BLACK;
grandfather->_col = RED;
}
break;
}
}
}
return true;
}
}
bool CheckColour(Node* root, int blacksum, int leftpathblack)
{
if (root == nullptr)
{
if (blacksum != leftpathblack)
{
cout << "每条路径上的黑色节点的数目不同" << endl;
return false;
}
return true;
}
Node* parent = root->_parent;
if (parent && parent->_col == RED && root->_col == RED)
{
cout << root->_kv.first << ':' << "出现两个连续的红节点" << endl;
return false;
}
if (root->_col == BLACK)
blacksum++;
return CheckColour(root->_left, blacksum, leftpathblack) &&
CheckColour(root->_right, blacksum, leftpathblack);
}
bool IsBalance()
{
return IsBalance(_root);
}
bool IsBalance(Node* root)
{
if (root == nullptr)
return true;
if (root->_col != BLACK)
{
cout << "根节点颜色错误不为黑色" << endl;
return false;
}
int leftpathbalck = 0;
Node* cur = root;
while (cur)
{
if (cur->_col == BLACK)
leftpathbalck++;
cur = cur->_left;
}
return CheckColour(root, 0, leftpathbalck);
}
int Height()
{
return Height(_root);
}
int Height(Node* root)
{
if (root == nullptr)
{
return 0;
}
int heightL = Height(root->_left);
int heightR = Height(root->_right);
return heightL > heightR ? heightL + 1 : heightR + 1;
}
private:
void RotateL(Node* parent)
{
_rotatesum++;
Node* ppnode = parent->_parent;
Node* cur = parent->_right;
Node* curleft = cur->_left;
parent->_right = curleft;
if (curleft)
{
curleft->_parent = parent;
}
cur->_left = parent;
parent->_parent = cur;
if (ppnode == nullptr)
{
_root = cur;
cur->_parent = nullptr;
}
else
{
cur->_parent = ppnode;
if (ppnode->_left == parent)
{
ppnode->_left = cur;
}
else
{
ppnode->_right = cur;
}
}
}
void RotateR(Node* parent)
{
_rotatesum++;
Node* ppnode = parent->_parent;
Node* cur = parent->_left;
Node* curright = cur->_right;
parent->_left = curright;
if (curright)
{
curright->_parent = parent;
}
cur->_right = parent;
parent->_parent = cur;
if (ppnode == nullptr)
{
_root = cur;
cur->_parent = nullptr;
}
else
{
if (ppnode->_left == parent)
{
ppnode->_left = cur;
cur->_parent = ppnode;
}
else
{
ppnode->_right = cur;
cur->_parent = ppnode;
}
}
}
private:
Node* _root;
public:
int _rotatesum = 0;
};



 浙公网安备 33010602011771号
浙公网安备 33010602011771号