ffmpeg 二叉树代码测试及分析 - 详解
author: hjjdebug
date : 2025年 11月 20日 星期四 08:57:46 CST
description: ffmpeg 二叉树代码测试及分析
文章目录
1 二叉树的概念.
二叉树每一个结点有2个孩子结点, 直到叶子结点.
叶子结点有2个指针为空的孩子结点.
左支的孩子结点,其key值小于父结点,右值的孩子结点,其key值大于父结点.
2 平衡的二叉树.
对所有结点,左右子树高度差不超过1 的二叉树叫平衡的二叉树.
3 考察3个结点的二叉树
考察3个结点构成的二叉树. 是的,树的结点数可以很多, 但3个结点是它的基本结构,
搞清楚了3个结点, 就基本搞清楚了树.
3.1 平衡的二叉树
3个结点, 平衡的2叉树结构只有一种. 它们每个结点高度差为0,如图示: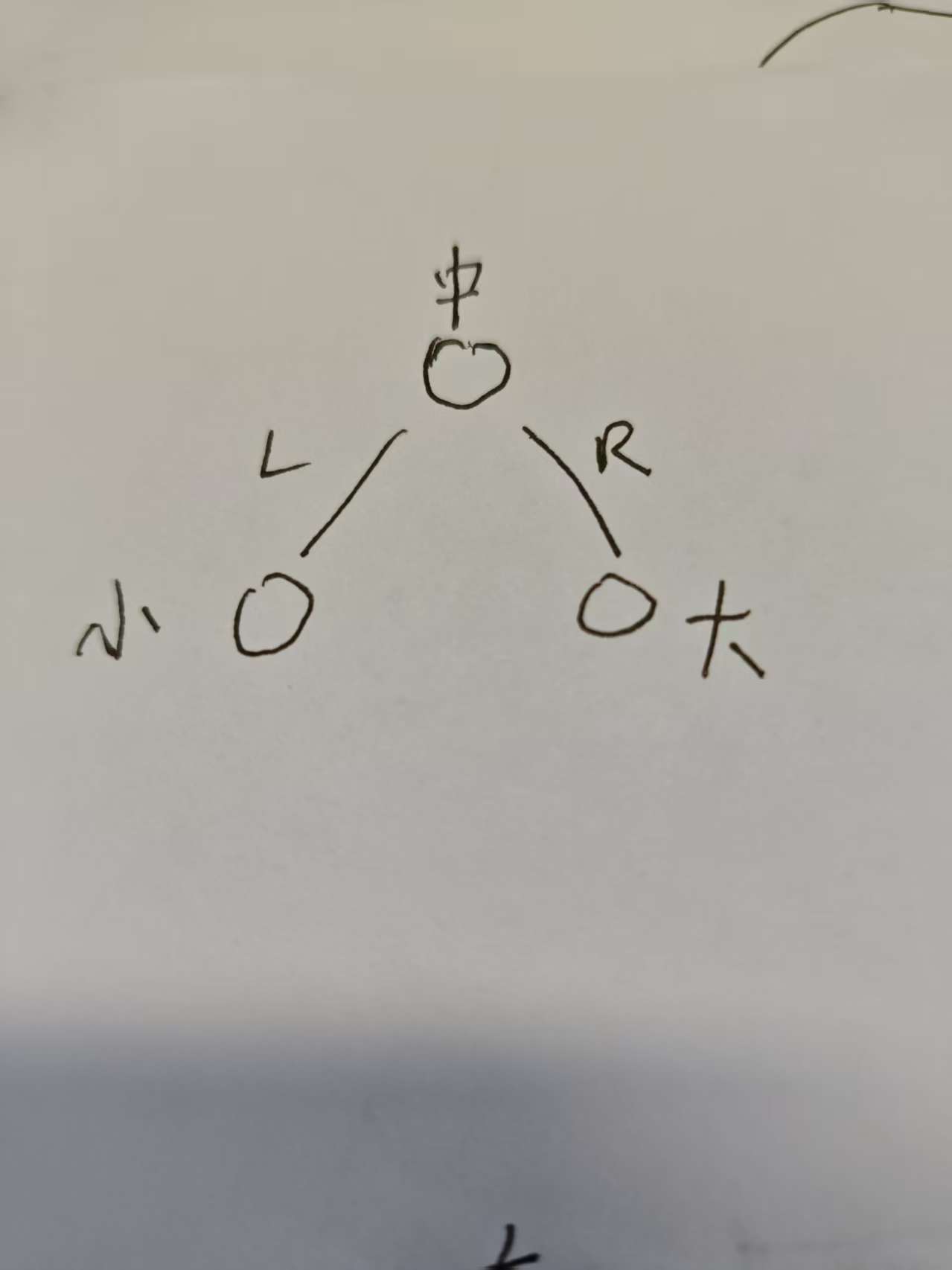
3.2 不平衡的二叉树
不平衡的2叉数有4种, 如图示. 它们高度差为2,所以是不平衡的.
根据路径,可称之为LL,LR,RL,RR, 其中LL与RR 对称, LR 与 RL 对称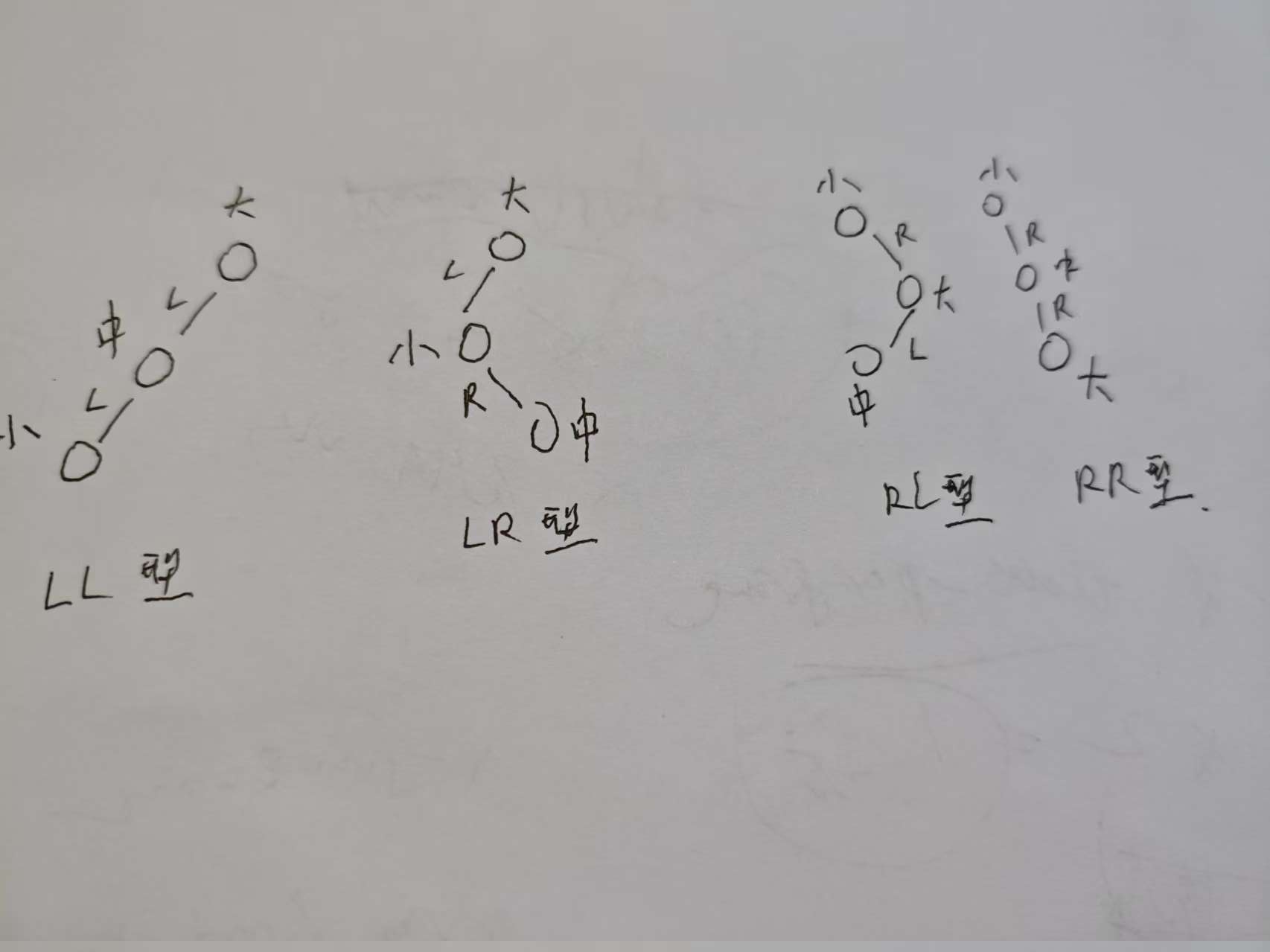
它们的共同特点是, 首个结点不是中结点,二是大结点或者小结点,不符合平衡树第一个结点是中结点的特点.
3.3 不平衡2叉数的调整
由于LL与RR 对称, LR 与 RL 对称, 所以4种只要搞懂了2种就够了.
LL 型的调整. 只要把中结点向上提一级,让大结点做它的右孩子就可以了, 看起来就像把顶部的大结点向右旋转了一下.
LR 型的调整. 此时的中结点是新加入的结点,它需要提高2级到第1结点位置,然后把小节点作为左支,把大节点作为右支.
看起来已不是简单的旋转了, 不过也仍然只是简单的调整.
4 ffmpeg 二叉树测试实例
ffmpeg 中实现了一种平衡的2叉树(AVL树), 我们看看它的使用方法
它的调用参数有点奇特,是为了减少接口所特意设计的.
测试用例如下. 测试代码把av_tree_insert()函数挪到了本地方便注释,调试
$ cat main.c
#include "libavutil/mem.h"
#include "libavutil/tree.h"
#include <stdint.h>
#include <stdio.h>
//技巧高能够使代码简洁, 可是阅读起来就比较吃力了, 写代码还是应该以易读为主要原则!!
//不过技巧好的也应该阅读
typedef struct AVTreeNode
{
struct AVTreeNode* child[2]; //child[2] 是二叉树节点的标准形式
void* elem; // 这里的elem 指针保留的是传入的 data,10,20,30之类的数据
int state; // state 保存的是右子树减左子树的差值,层高差值
} AVTreeNode;
static void print(AVTreeNode* t, int depth)
{
int i;
// depth 负责打印缩进,可以分清父节点和子节点
for (i = 0; i < depth * 4; i++)
printf(" ");
if (t)
{
printf("Node %p %2d %ld\n", t, t->state, (long int)t->elem);
print(t->child[0], depth + 1);
print(t->child[1], depth + 1);
}
else //节点指针为空时,打印NULL
printf("NULL\n");
}
// 这里的指针a, 指针b, 就是传入的数据. b是待插入的节点即key 值
static int cmp(const void* a, const void* b)
{
return (const uint8_t*)a - (const uint8_t*)b;
}
void* av_tree_insert(AVTreeNode** tp, void* key,
int (*cmp)(const void* key, const void* b), AVTreeNode** next)
{
// *tp, t 是顶部节点指针
AVTreeNode* t = *tp;
if (t) // top节点不为空的情况,要继续查找位置
{ // 例如考虑v 比较为负值,向右child插入的情景
unsigned int v = cmp(t->elem, key);
void* ret;
if (!v) //比较结果为相等
{
if (*next) // 如果*next 有值,就不用插入了,直接返回t->elem值
return t->elem;
else if (t->child[0] || t->child[1])
{ //如果该节点下有子结点,
int i = !t->child[0];//child[0]不为空,则i=0,从左支查找,否则,i=1从右支查找
void* next_elem[2];
av_tree_find(t->child[i], key, cmp, next_elem);
//这里修改了key 和 t->elem,把自己伪装成下一个元素, 后续执行insert从而把该节点删除,并调整了树平衡
key = t->elem = next_elem[i];
v = -i;
}
else
{ // *next 为空,是要删除包含key的节点,那就把节点返回去
*next = t;
*tp = NULL; //把节点指针变成NULL,这是节点没有左右子节点的情况
return NULL;
}
}
// v>>31 v=正数,v>>31=0, v=负数, v>>31=1, v是比较的返回值
// 先考察v为负值,向右边找的情景,递归会找到空子节点
ret = av_tree_insert(&t->child[v >> 31], key, cmp, next); // 这里递归调用
// 下面代码时递归返回的代码
if (!ret)
{ // 返回NULL 是新节点已插入
int i = (v >> 31) ^ !!*next; // 比较为负值且next为空,右子树在增高i=1
AVTreeNode** child = &t->child[i]; // child 是我们关注的那个child
t->state += 2 * i - 1; // 更新top节点高度差,可能加1或者减1
// 判定top 节点是否需要调整
if (!(t->state & 1)) // 当t->state 为偶数时
{
if (t->state)// 当t->state为真时, 例如t->state==2, 就需要调整节点了
{
//调整节点,我宁愿分四种情况写, 可是它按2种情况混合着写,代码短了点,但很难读
//因为首先要确定这个i
//问题2: (*child)->state是什么时候改变的?也是在71行t->state处改变的
// child 也会在递归中做顶部节点,递归函数好难调试,算法混在一块也不清晰,只是为了简洁
if ((*child)->state * 2 == -t->state) //例如RL类型, t->state==2,(*child)->state==-1
{ //2叉树是对指针操作的考验!
*tp = (*child)->child[i ^ 1]; //child 的左支做顶层,提升2级
(*child)->child[i ^ 1] = (*tp)->child[i];
(*tp)->child[i] = *child; //把child 做顶层右支
*child = (*tp)->child[i ^ 1]; //顶层左支送child
(*tp)->child[i ^ 1] = t; //旧顶层做新顶层左支
//调整新顶层及其2个child 的层高差. 写法有点难读!
(*tp)->child[0]->state = -((*tp)->state > 0);
(*tp)->child[1]->state = (*tp)->state < 0;
(*tp)->state = 0;
}
else
{ // 例如单调递增代码,i为1, RR调整
// 例如10,20,30中,10为t,20为child,30为child[1], *tp为新top,指向20
*tp = *child; // child 提高1层, 送新top
*child = (*child)->child[i ^ 1]; // child 左支送child
(*tp)->child[i ^ 1] = t; // 原来的top送新top(*tp) 的左支
//更新state
if ((*tp)->state) // 根据新tp, 调整原始top的state
t->state = 0;
else
t->state >>= 1;
(*tp)->state = -t->state; // 设置新top的state
}
}
}
//比较的是(*tp)->state 布尔值与 *next 布尔值相同返回1,例如state==0,*next==0
if (!(*tp)->state ^ !!*next)
return key; // 从这里返回,代表什么? 代表不用调整节点
}
return ret; // 这个ret 是递归 av_tree_insert 的 ret; 如果为空需要计算层差并判断是否需要调整平衡
}
else // 递归后总能找到空子节点 *tp==0
{
*tp = *next; // 新节点接到它的空节点处
*next = NULL; //*next 指针赋空表示已使用,并返回NULL
if (*tp)
{
(*tp)->elem = key; // 并把key值赋值给top节点, 如果不是一招2用,本来上层应该直接赋值的.
return NULL;
}
else
return key; // 返回是树中节点保留的数值
}
}
// 传入整数数据, 把数据挂到树上, 保持树的平衡.
void testTree(int* data, int length)
{
AVTreeNode *root = NULL, *node = NULL;
int i;
for (i = 0; i < length; i++)
{
printf("inserting %4d\n", data[i]);
// 分配一个结点
if (!node)
node = av_tree_node_alloc();
if (!node)
{
printf("Memory allocation failure.\n");
return;
}
// 把数据插入到结点上
// 这个接口有点怪! 它没有直接把data[i] 赋值给node->element, 而是分开传.反人类.
// 为什么这样呢? 因为这个insert 也是delete接口, 当node=NULL时, 要delete 数值是data[i]的节点
av_tree_insert(&root, (void*)(long)data[i], cmp, &node);
// 第一次root为空, 插完第一个节点, root 指针改变为第一个节点地址
print(root, 0); // 打印整个树
}
av_free(node);
av_tree_destroy(root);
}
void testRemove()
{
AVTreeNode *root = NULL;
AVTreeNode *node = av_tree_node_alloc();
int i=50;
av_tree_insert(&root, (void*)(long)i, cmp, &node);
if(node==NULL)
node=av_tree_node_alloc();
int j=100;
printf("adding %4d\n", j);
av_tree_insert(&root, (void *)(long)(j), cmp, &node);
printf("removing %4d\n", i);
AVTreeNode *node2 = NULL;
av_tree_insert(&root, (void *)(long)(i), cmp, &node2);
void * k = av_tree_find(root, (void *)(long)i, cmp, NULL);
if (k)
printf("removal failure %d\n", j);
av_free(node2);
}
int RR_data[] = { 10, 20, 30, 40, 50 }; // 数据是精心准备的,这是单调递增,必需要调整树,左旋使平衡
int RR_data_size = sizeof(RR_data) / sizeof(RR_data[0]);
int RL_data[] = { 10, 100, 20, 150, 110 }; // 数据是精心准备的,这是波浪递增,必需要调整树使平衡
int RL_data_size = sizeof(RL_data) / sizeof(RL_data[0]);
int main()
{
testTree(RR_data, RR_data_size); // 测试单调递增
// testTree(RL_data, RL_data_size); //测试波浪递增
// testRemove();
return 0;
}4.1 执行结果:
单调递增测试:
$ ./t2
inserting 10
Node 0x5da73a56e040 0 10
NULL
NULL
inserting 20
Node 0x5da73a56e040 1 10
NULL
Node 0x5da73a56e0c0 0 20
NULL
NULL
inserting 30
Node 0x5da73a56e0c0 0 20
Node 0x5da73a56e040 0 10
NULL
NULL
Node 0x5da73a56e140 0 30
NULL
NULL
inserting 40
Node 0x5da73a56e0c0 1 20
Node 0x5da73a56e040 0 10
NULL
NULL
Node 0x5da73a56e140 1 30
NULL
Node 0x5da73a56e1c0 0 40
NULL
NULL
inserting 50
Node 0x5da73a56e0c0 1 20
Node 0x5da73a56e040 0 10
NULL
NULL
Node 0x5da73a56e1c0 0 40
Node 0x5da73a56e140 0 30
NULL
NULL
Node 0x5da73a56e240 0 50
NULL
NULL波浪递增测试:
./t2
inserting 10
Node 0x57ec61470040 0 10
NULL
NULL
inserting 100
Node 0x57ec61470040 1 10
NULL
Node 0x57ec614700c0 0 100
NULL
NULL
inserting 20
Node 0x57ec61470140 0 20
Node 0x57ec61470040 0 10
NULL
NULL
Node 0x57ec614700c0 0 100
NULL
NULL
inserting 150
Node 0x57ec61470140 1 20
Node 0x57ec61470040 0 10
NULL
NULL
Node 0x57ec614700c0 1 100
NULL
Node 0x57ec614701c0 0 150
NULL
NULL
inserting 110
Node 0x57ec61470140 1 20
Node 0x57ec61470040 0 10
NULL
NULL
Node 0x57ec61470240 0 110
Node 0x57ec614700c0 0 100
NULL
NULL
Node 0x57ec614701c0 0 150
NULL
NULL5 ffmpeg 二叉树算法代码.
ffmpeg 中的代码简洁干练,所以我特别标注了它的insert算法. 其它函数比较简单
把av_tree_insert() 挪到了用户的代码空间, 方便调试和注释.
5.1 av_tree_insert() 函数调用参数
void* av_tree_insert(AVTreeNode** tp, void* key,
int (cmp)(const void key, const void* b), AVTreeNode** next)
第一参数: top顶层node指针的地址, 意味着执行完插入,这个地址可能会改变.
第二参数: 插入的数据,
第三参数: 用户自定义的比较算法,传参a,是内部节点的数据, 传参b,就是用户待插入的数据key了.
第四参数: 这是个容易误解的东西. 如果next 为真, 是把key 插入到树,
如果next为NULL,是把包含key值的节点从树中删除.
5.2 程序技巧
- 删除节点时, 如果该节点有子节点, 它把自己的值先改成叶子结点的值,把key值也改成叶子节点的值,
继续执行av_tree_insert, 引起比较返回0值,从而删除该节点并调整了树平衡. - 维持树平衡代码它把4种情况按2种情况来写,用变量i来区分左右,代码简洁但逻辑有点难读.
除了看代码注释还是要调试才能理解代码. 标注信息都写在测试代码中了,就不再这里赘述了.




 浙公网安备 33010602011771号
浙公网安备 33010602011771号