实用指南：《算法通关指南：算法基础篇 --- 一维前缀和（1）—1. 【模板】前缀和，2.最大子段和》

《算法通关指南：算法基础篇 ---- 一维前缀和— 1. 【模板】前缀和，2.最大子段和》

---

小龙报：个人主页
作者简介：C++研发，嵌入式，机器人方向学习者
❄️个人专栏：《C语言》《算法》KelpBar海带Linux智慧屏项目
《coze智能体开发平台》
✨永远相信美好的事情即将发生

文章目录

• 《算法通关指南：算法基础篇 ---- 一维前缀和— 1. 【模板】前缀和，2.最大子段和》
• 前言
• 一、前缀和
• 二、一维前缀和
• • 2.1 核心问题
  • • 2.1.1 构建一维前缀和
    • 2.2.2 利用前缀和数组求解区间【l，r】内元素的和
  • 三、一维前缀和经典算法题
  • 3.1【模板】前缀和
  • • 3.1.1题目
    • 3.1.2 算法原理
    • 3.1.3代码
  • 3.2 最大子段和
  • • 3.2.1 题目
    • 3.2.2 算法原理
    • 3.2.3 代码
• 总结与每日励志

---

前言

本系列讲解算法竞赛的数据结构在算法竞赛中，我们主要关心的其实是时间开销，空间上是基本够用的，因此我们是使用庞大的数组实现的话不多说冲！

---

一、前缀和

前缀和与差分的核心思想是预处理，可以在暴力枚举的过程中，快速给出查询的结果，从而优化时间复杂度。是经典的用空间替换时间的做法

二、一维前缀和

2.1 核心问题

2.1.1 构建一维前缀和

核心公式：f[i] = f[i − 1] + a[i]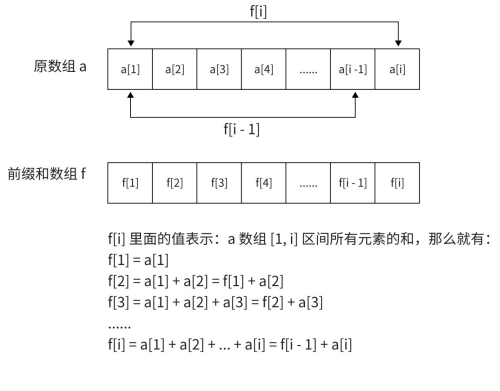

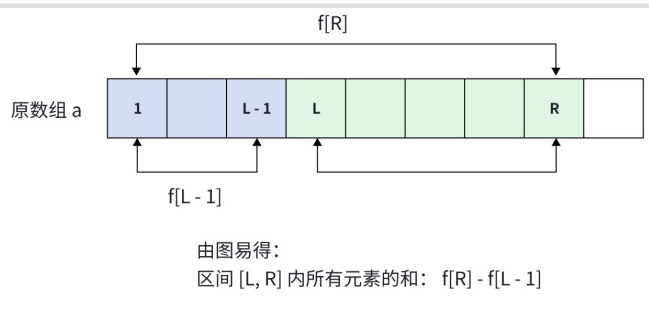
2.2.2 利用前缀和数组求解区间【l，r】内元素的和

核心公式：f[r] − f[l − 1]

三、一维前缀和经典算法题

3.1【模板】前缀和

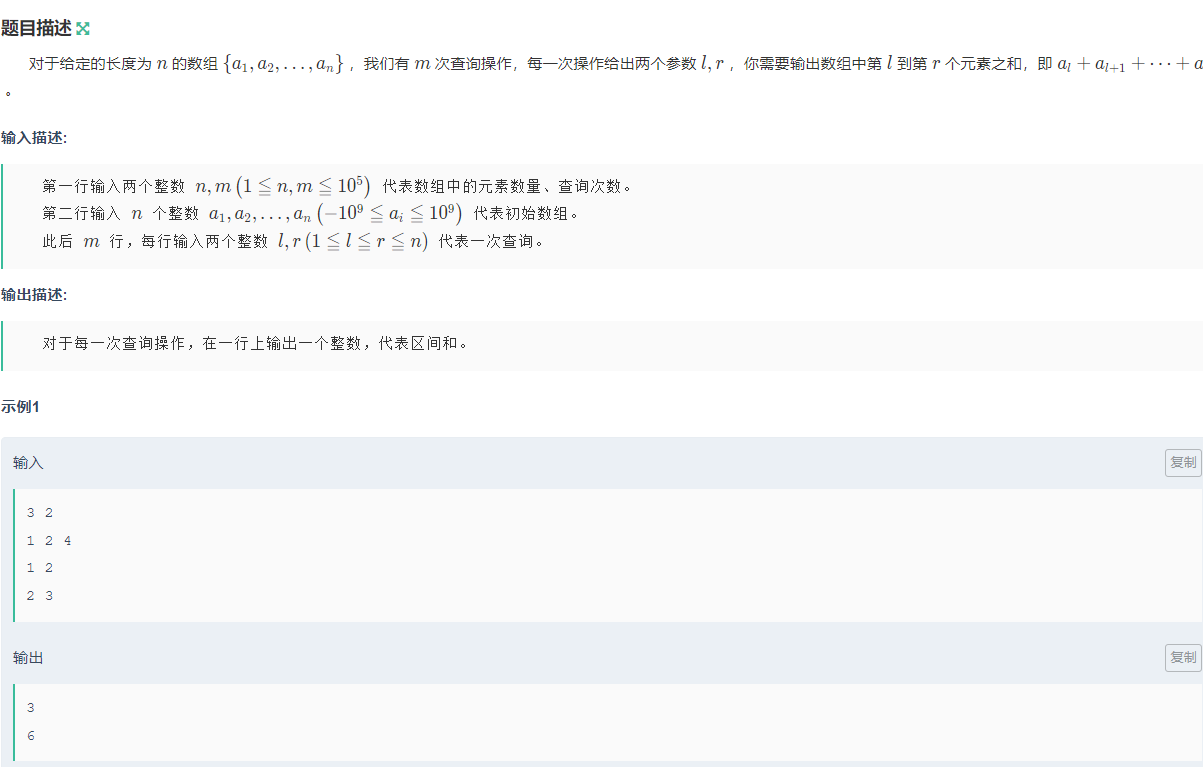
3.1.1题目

链接：【模板】前缀和

3.1.2 算法原理

依照刚才讲解前缀和原理模拟即可

3.1.3代码

#include <iostream>
  using namespace std;
  const int N = 1e5 + 10;
  typedef long long LL;  //数组大小最大1e9相加会超过int，故用long long
  LL a[N];
  LL f[N]; //前缀和数组
  int main()
  {
  int n,m;
  cin >> n >> m;
  for (int i = 1; i <= n; i++)
  cin >> a[i];
  //从1开始，f[i - 1] = f[0] = 0，可以有效避免i - 1 = -1 使得数组越界 
  for (int i = 1; i <= n; i++)
  f[i] = f[i - 1] + a[i];
  while (m--)
  {
  int l, r;
  cin >> l >> r;
  //[l,r]区间
  cout << f[r] - f[l - 1] << endl;
  }
  return 0;
  }

3.2 最大子段和

3.2.1 题目

链接：最大子段和

3.2.2 算法原理

考虑以i 位置的元素a[i] 「为结尾」的最大子段和：
• 如果想要最大子段和，也就是最大区间和，那么用f[i] 减掉⼀个前驱最小值即可。
因此，我们可以创建前缀和数组，然后在遍历前缀和数组的过程中，⼀边更新前驱最小值，⼀边更新当前位置为结尾的最大子段和。

3.2.3 代码

#include <iostream>
  using namespace std;
  const int N = 2e5 + 10;
  typedef long long LL;
  LL f[N]; //构建前缀和数组
  int main()
  {
  int n;
  cin >> n;
  for (int i = 1; i <= n; i++)
  {
  int x;
  cin >> x;
  f[i] = f[i - 1] + x;
  }
  LL ret = -1e20;  //前缀和可能为负数
  LL pre = 0;  //以1为结尾的前缀和前驱最小为0
  for (int i = 1; i <= n; i++)
  {
  ret = max(ret, f[i] - pre);
  pre = min(pre, f[i]); //寻找【1，i】区间的最小值
  }
  cout << ret << endl;
  return 0;
  }

总结与每日励志

✨本文讲解了算法竞赛中的一维前缀和算法，通过预处理数组实现快速区间查询，有效优化时间复杂度。文章详细介绍了前缀和的核心公式（f[i] = f[i-1] + a[i]）和区间求和公式（f[r]-f[l-1]），并通过两个典型例题《前缀和模板》和《最大子段和》进行实战演示，展示了如何用前缀和思想解决实际问题。最后以"永远相信美好的事情即将发生"作为励志结语，鼓励读者坚持算法学习。全文简洁清晰，兼顾理论讲解与代码实现，适合算法初学者参考学习。