第十四章聚类方法理论及Python完成

文章目录

• 1.基本概念
• • 1.1 距离or相似度
  • 1.2 类或簇
  • 1.3 类与类之间的距离
• 2. 层次聚类算法基本理论
• • 2.1 Python代码实现层次分析法例题
• 3. K均值聚类方法
• • 3.1 K均值算法特性
  • 3.2 Python实现K均值

聚类是针对给定的样本，依据它们特征的相似度或距离，将其归并到若干个“类”或“簇”的数据分析问题。属于无监督学习，核心思路是让同一簇内样本相似度高、不同簇间相似度低。聚类的算法包括很多，常见的可以总结为下表：

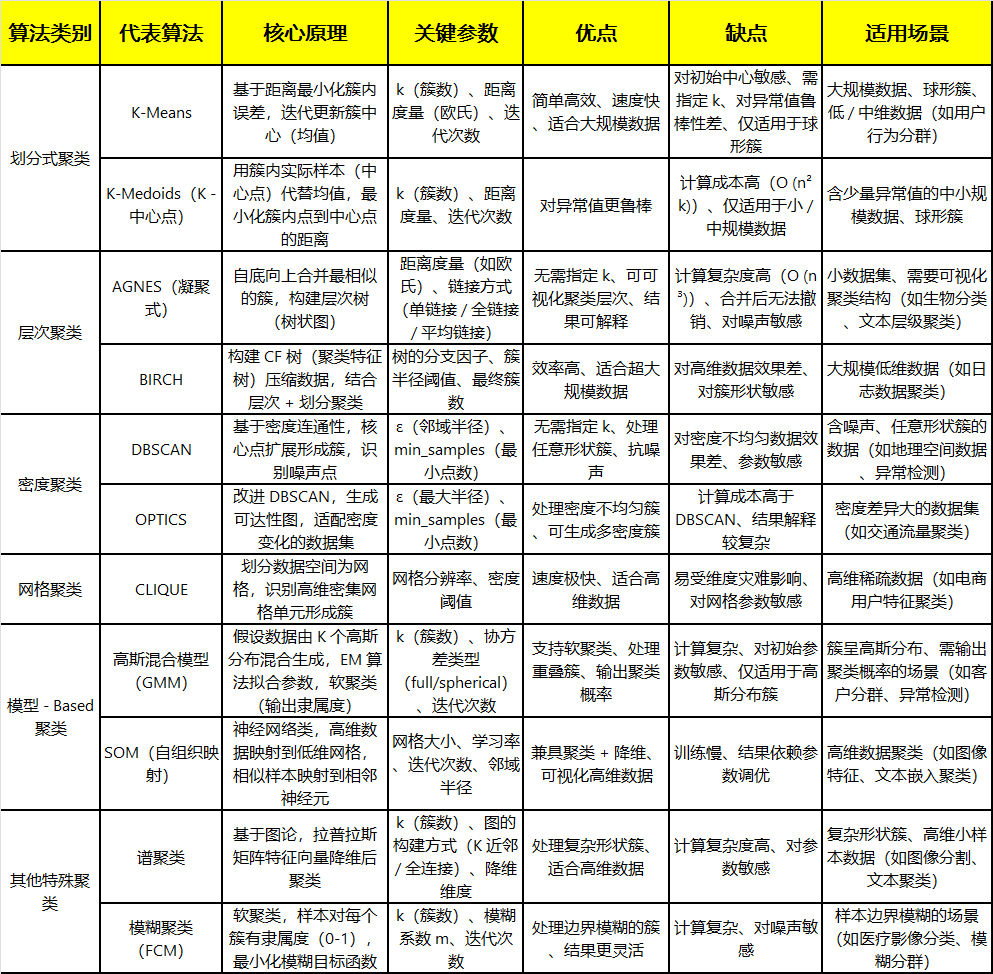
归其根本是聚类的核心概念是距离或相似度，有多种相似度或距离的定义，相似度直接影响聚类的结果，所以其选择是聚类的根本问题。下面对“相似度或距离”进行介绍：

1.基本概念

1.1 距离or相似度

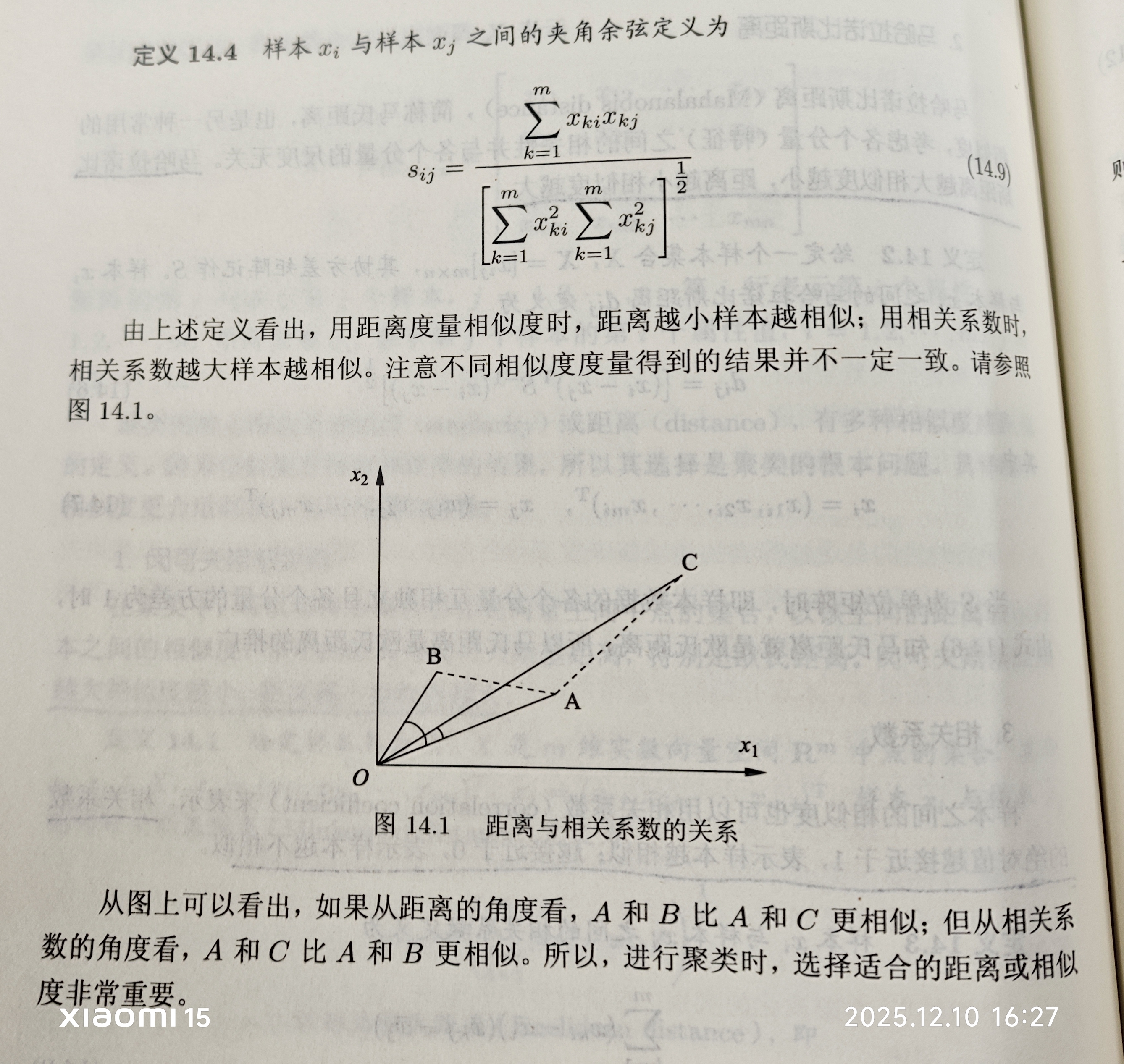
1.2 类或簇

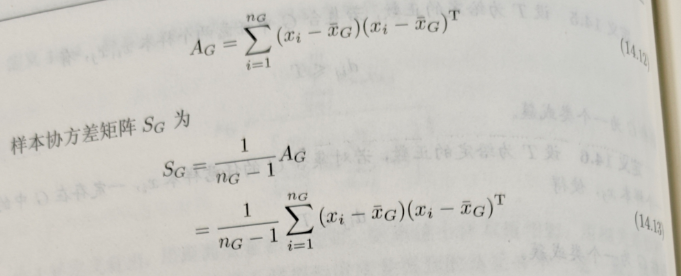
1.3 类与类之间的距离

2. 层次聚类算法基本理论

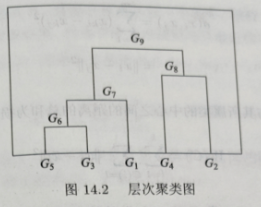
2.1 Python代码实现层次分析法例题

import numpy as np
import matplotlib.pyplot as plt
from scipy.cluster.hierarchy import linkage, dendrogram, fcluster
# 1. 定义距离矩阵
# 输入的5×5距离矩阵（样本0-4）
distance_matrix = np.array([
[0, 7, 2, 9, 3],
[7, 0, 5, 4, 6],
[2, 5, 0, 8, 1],
[9, 4, 8, 0, 5],
[3, 6, 1, 5, 0]
])
# 2. 生成层次聚类的"链接矩阵"（凝聚式，基于距离矩阵）
from scipy.spatial.distance import squareform
condensed_dist = squareform(distance_matrix)
# 执行凝聚式层次聚类（方法：平均链接，也可选single/complete等）
linkage_matrix = linkage(condensed_dist, method='average')  # method可选：single/complete/average
plt.figure(figsize=(8, 5))
dendrogram(
linkage_matrix,
labels=[f"样本{i}" for i in range(5)],  # 样本标签
leaf_rotation=0,  # 标签旋转角度
leaf_font_size=12,
color_threshold=3,  # 聚类颜色阈值（可调整）
above_threshold_color='gray'
)
plt.title('层次聚类树状图（平均链接）')
plt.xlabel('样本')
plt.ylabel('距离')
plt.tight_layout()
plt.show()
# 4. 从层次聚类中提取指定簇数的聚类结果
n_clusters = 2  # 目标簇数
clusters = fcluster(linkage_matrix, t=n_clusters, criterion='maxclust')
print(f"各样本的聚类结果（簇数={n_clusters}）：")
for i in range(5):
print(f"样本{i} → 簇{clusters[i]}")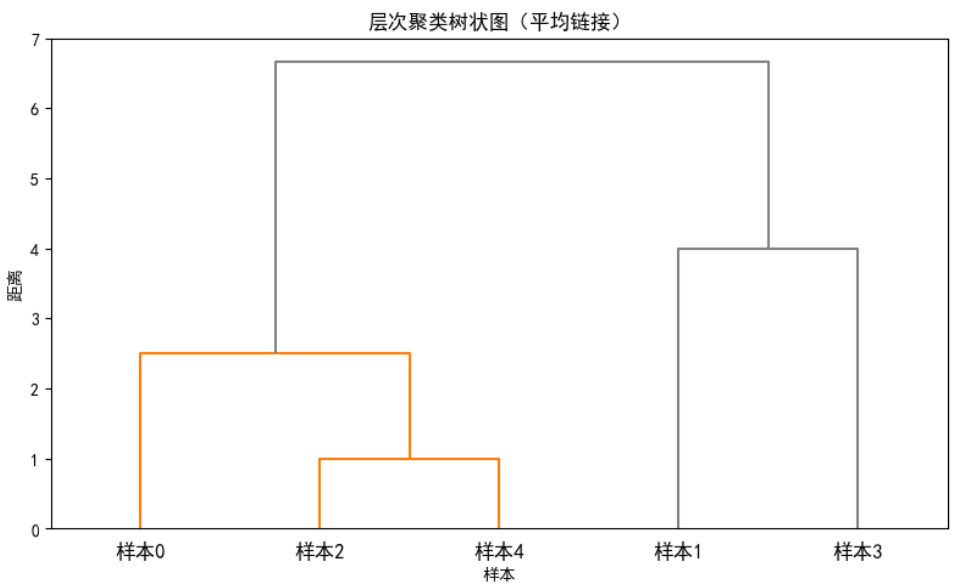

3. K均值聚类方法

3.1 K均值算法特性

总的来说，K均值的和核心优点：

1. 简单高效：算法逻辑直观（迭代分配样本 +更新中心），时间复杂度低（通常为(O(nkt))，n是样本数、k是簇数、t是迭代次数）；
2. 适合大规模数据。易实现与调参仅需指定簇数k和距离度量（常用欧氏距离），参数少、工程落地成本低；
3. 结果易解释:簇中心（均值）可直接作为簇的“代表”，便于理解每个簇的特征（如用户分群中，簇中心对应典型用户的行为特征）。

缺点有：

1. 对初始中心敏感：随机选择的初始簇中心可能导致不同的聚类结果（易陷入局部最优），需通过 “K-Means++”（优化初始中心选择）缓解。
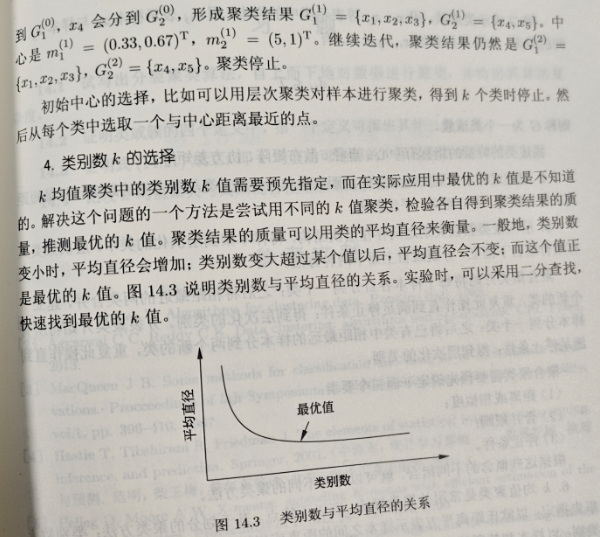
2. 需预先指定簇数k：k的选择依赖经验（可通过肘部法则、轮廓系数辅助，但无绝对标准），选不好会直接影响聚类效果。
3. 对数据分布有局限：仅适用于球形、密度均匀的簇，对非球形（如环形）、密度差异大的簇效果差。
4. 抗噪声异常值能力弱：簇中心是均值，异常值会显著 “拉偏” 中心，导致聚类结果失真。

3.2 Python实现K均值

import numpy as np
from sklearn.cluster import KMeans
import matplotlib.pyplot as plt
X = np.array([
[0, 2],   # 样本0（作为第一个初始簇中心）
[0, 0],   # 样本1（作为第二个初始簇中心）
[1, 0],   # 样本2
[5, 0],   # 样本3
[5, 2]    # 样本4
])
sample_labels = [f"样本{i}" for i in range(5)]  # 样本标签
# 2. 手动指定初始簇中心：前两个样本（样本0和样本1）
init_centers = X[:2]  # 取前两个样本作为初始中心
print("=== 手动指定的初始簇中心 ===")
print(f"初始中心1（样本1）：{init_centers[0]}")
print(f"初始中心2（样本2）：{init_centers[1]}")
# 3. 初始化并训练K-Means模型（指定初始中心）
kmeans = KMeans(
n_clusters=2,        # 簇数固定为2（匹配初始中心数量）
init=init_centers,   # 手动指定初始簇中心（核心修改点）
n_init=1,            # 仅运行1次（因为手动指定了初始中心，无需多次初始化）
random_state=42      # 固定随机种子，结果可复现
)
y_pred = kmeans.fit_predict(X)  # 拟合数据并预测簇标签
# 4. 输出核心结果
print("\n=== K均值聚类最终结果 ===")
print(f"最终簇中心：\n{kmeans.cluster_centers_}")
print(f"簇内平方和（SSE）：{kmeans.inertia_:.2f}")  # 评估簇内紧凑度
print("\n各样本的簇分配：")
for sample, label in zip(sample_labels, y_pred):
print(f"{sample} → 簇{label}")
# 5. 可视化聚类过程与结果（含初始中心+最终中心）
plt.figure(figsize=(10, 7))
# 绘制所有样本点
scatter = plt.scatter(
X[:, 0], X[:, 1],
c=y_pred, s=120, cmap='viridis', alpha=0.8, edgecolors='black'
)
# 绘制初始簇中心（蓝色三角形，区分最终中心）
plt.scatter(
init_centers[:, 0],
init_centers[:, 1],
c='blue', s=300, marker='^', label='初始中心（样本0/1）', edgecolors='black'
)
# 绘制最终簇中心（红色星号）
plt.scatter(
kmeans.cluster_centers_[:, 0],
kmeans.cluster_centers_[:, 1],
c='red', s=300, marker='*', label='最终簇中心', edgecolors='black'
)
# 标注每个样本的编号
for i, sample in enumerate(sample_labels):
plt.text(X[i,0]+0.1, X[i,1]+0.1, sample, fontsize=12, fontweight='bold')
# 图表美化
plt.xlabel('特征1', fontsize=12)
plt.ylabel('特征2', fontsize=12)
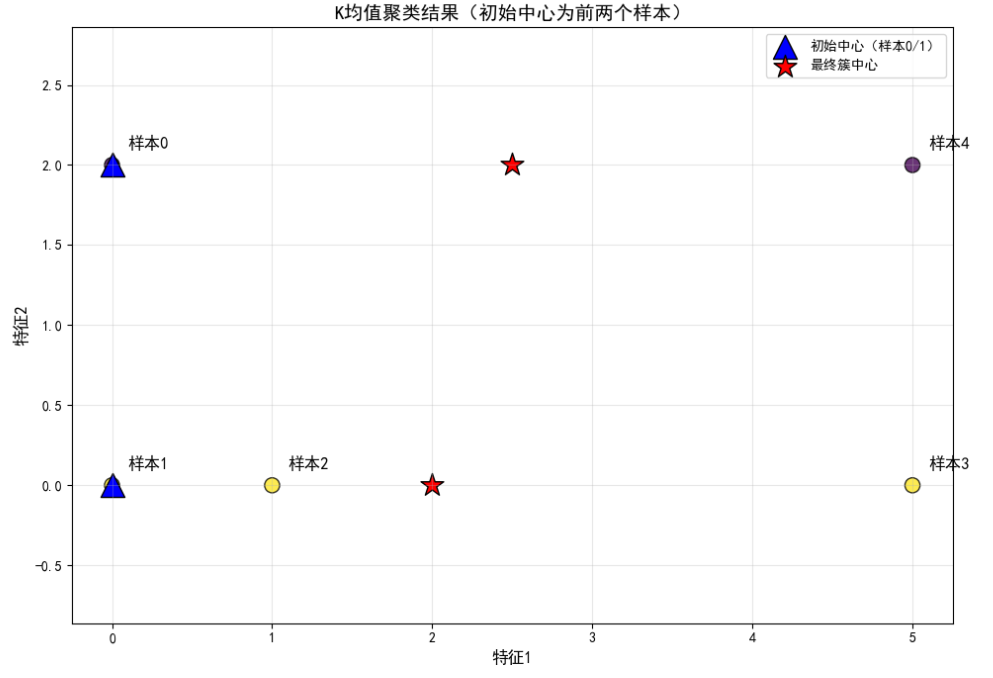
plt.title('K均值聚类结果（初始中心为前两个样本）', fontsize=14)
plt.grid(alpha=0.3)  # 网格线增强可读性
plt.legend(loc='upper right')
plt.axis('equal')    # 等比例坐标轴，避免视觉变形
plt.tight_layout()
plt.show()在这里插入代码片

这里的样本0和样本4对应书中的样本1和样本5