ABC437F

ABC437 讲解

F - Manhattan Christmas Tree 2

题目概要：

给定n个点(xi,yi)

Q组询问，两个操作

操作1：修改第i个点的坐标

操作2：查询区间内所有点到给定点的曼哈顿距离最大值

首先看到这个题目，单点修，区间查，加上2e5的数据范围，很难让人不想到线段树

但是线段树没法直接维护两点之间的曼哈顿距离

这是考虑一个经典的思路：求哈夫曼距离时，将图旋转45度

具体的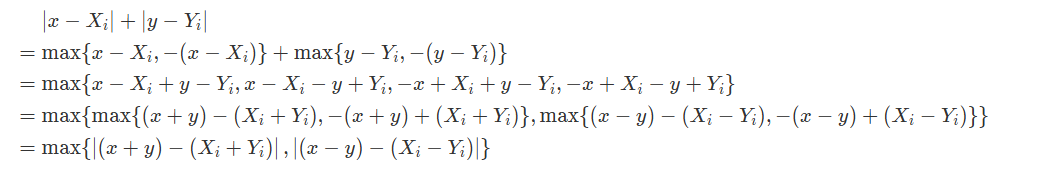

这个时候我们再看查询操作就很好办了

每次询问区间哈夫曼距离最大值，其实就是求

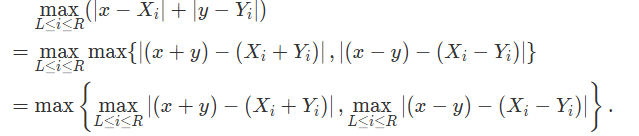
这个时候查询就很好看了

将每个点（包括给定点）的二元组转化成（x+y,x-y）的形式加入线段树

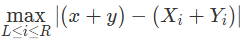
这个东西最大一定是(Xi+Yi)最大或最小，因为x+y是定值（别忘了绝对值）

后面同理

于是开两个线段树分别记录x+y的最大值和最小值，x-y的最大值和最小值

单点修改，区间查询最大最小值即可

时间复杂度O(qlogn)

Code（我的线段树直接粘的模版，因为本人不太会线段树，所以代码会有些冗余，大概理解思路就行）

#include<iostream>
#include<cstdio>
#include<cstdlib>
#include<cstring>
#include<cmath>
#include<algorithm>
#include<iomanip>
#include<bits/stdc++.h>
#define int long long
#define lson x<<1
#define rson x<<1|1
using namespace std;
inline int read()
{
	int x=0,f=1;char ch=getchar();
	while (ch<'0'||ch>'9'){if (ch=='-') f=-1;ch=getchar();}
	while (ch>='0'&&ch<='9'){x=x*10+ch-48;ch=getchar();}
	return x*f;
}
struct node{
	int maxx,minn;
	int add;
	node(){
		add=0;
		minn=1e18;
		maxx=-1e18;
	}
	void chu(int v){
		minn=maxx=v;
	}
}tr1[800005],tr2[800005];
int a[200005],b[200005],n,q;
node operator+(const node &l,const node &r){
	node ans;
	ans.maxx=max(l.maxx,r.maxx);
	ans.minn=min(l.minn,r.minn);
	return ans;
}
void color1(int l,int r,int x,int v){
	tr1[x].add+=v;
	tr1[x].maxx+=v;
	tr1[x].minn+=v;
}
void pushdown1(int l,int r,int x){
	int mid=(l+r)>>1;
	color1(l,mid,lson,tr1[x].add);
	color1(mid+1,r,rson,tr1[x].add);
	tr1[x].add=0;
}
void color2(int l,int r,int x,int v){
	tr2[x].add+=v;
	tr2[x].maxx+=v;
	tr2[x].minn+=v;
}
void pushdown2(int l,int r,int x){
	int mid=(l+r)>>1;
	color2(l,mid,lson,tr1[x].add);
	color2(mid+1,r,rson,tr1[x].add);
	tr2[x].add=0;
}
void build(int l,int r,int x){
	if(l==r){
		tr1[x].chu(a[l]);
		tr2[x].chu(b[l]);
		return ;
	}
	int mid=(l+r)>>1;
	build(l,mid,lson);
	build(mid+1,r,rson);
	tr1[x]=tr1[lson]+tr1[rson];
	tr2[x]=tr2[lson]+tr2[rson];
}
node query1(int l,int r,int x,int nl,int nr){
	if(nl<=l&&r<=nr) return tr1[x];
	pushdown1(l,r,x);
	int mid=(l+r)>>1;
	if(nl<=mid){
		if(mid<nr) return query1(l,mid,lson,nl,nr)+query1(mid+1,r,rson,nl,nr);
		else return query1(l,mid,lson,nl,nr);
	}
	else return query1(mid+1,r,rson,nl,nr);
}
node query2(int l,int r,int x,int nl,int nr){
	if(nl<=l&&r<=nr) return tr2[x];
	pushdown2(l,r,x);
	int mid=(l+r)>>1;
	if(nl<=mid){
		if(mid<nr) return query2(l,mid,lson,nl,nr)+query2(mid+1,r,rson,nl,nr);
		else return query2(l,mid,lson,nl,nr);
	}
	else return query2(mid+1,r,rson,nl,nr);
}
void modify1(int l,int r,int x,int nl,int nr,int v){
	if(nl<=l&&r<=nr){
		color1(l,r,x,v);
		return ;
	}
	pushdown1(l,r,x);
	int mid=(l+r)>>1;
	if(nl<=mid) modify1(l,mid,lson,nl,nr,v);
	if(mid<nr) modify1(mid+1,r,rson,nl,nr,v);
	tr1[x]=tr1[lson]+tr1[rson];
}
void modify2(int l,int r,int x,int nl,int nr,int v){
	if(nl<=l&&r<=nr){
		color2(l,r,x,v);
		return ;
	}
	pushdown2(l,r,x);
	int mid=(l+r)>>1;
	if(nl<=mid) modify2(l,mid,lson,nl,nr,v);
	if(mid<nr) modify2(mid+1,r,rson,nl,nr,v);
	tr2[x]=tr2[lson]+tr2[rson];
}
signed main()
{
	//freopen("filename.in", "r", stdin);
	//freopen("filename.out", "w", stdout);
	n=read(),q=read();
	for(int i=1;i<=n;i++){
		int x=read(),y=read();
		a[i]=x+y;
		b[i]=x-y;
	} 
	build(1,n,1);
	while(q--){
		int opt,x,y;
		opt=read();
		if(opt==1){
			int i=read();
			x=read(),y=read();
			modify1(1,n,1,i,i,x+y-a[i]);
			modify2(1,n,1,i,i,x-y-b[i]);
			a[i]=x+y;
			b[i]=x-y;
		}
		else{
			int l=read(),r=read();
			x=read(),y=read();
			node an1=query1(1,n,1,l,r);
			node an2=query2(1,n,1,l,r);
			int ann1=max(abs(x+y-an1.minn),abs(an1.maxx-(x+y)));
			int ann2=max(abs(x-y-an2.minn),abs(an2.maxx-(x-y)));
			cout<<max(ann1,ann2)<<'\n';
		}
	}
	return 0;
}