pyyzDay10

数据结构选讲

T1 [HAOI2007] 修筑绿化带

考虑对每个外层矩阵B选最小的C

单调队列套一个单调队列

T2 「EZEC-14」众数 II

发现[l,r]的众数只可能是1/l

若l后面每一段结尾有任意一个<l，则答案一定是1

否则是l

考虑计算答案

倒序枚举值域l

每次维护极长的区间的区间和，S

合并时计算差值即可

T3 三步必杀

差分套差分

#include<iostream>
#include<cstdio>
#include<cstdlib>
#include<cstring>
#include<cmath>
#include<algorithm>
#include<iomanip>
#include<bits/stdc++.h>
#define jiaa(a,b) {a+=b;if(a>=MOD) a-=MOD;}
#define jian(a,b) {a-=b;if(a<0) a+=MOD;}
using namespace std;
int ksm(int a,int b,int p){
	if(b==0) return 1;
	if(b==1) return a%p;
	int c=ksm(a,b/2,p);
	c=c*c%p;
	if(b%2==1) c=c*a%p;
	return c%p;	
}
inline int read()
{
	int x=0,f=1;char ch=getchar();
	while (ch<'0'||ch>'9'){if (ch=='-') f=-1;ch=getchar();}
	while (ch>='0'&&ch<='9'){x=x*10+ch-48;ch=getchar();}
	return x*f;
}
int ch[10000005],cha[10000005];
signed main()
{
	//freopen("filename.in", "r", stdin);
	//freopen("filename.out", "w", stdout);
	int n=read(),m=read();
	while(m--){
		int l=read(),r=read(),s=read(),e=read();
		ch[l]+=s;
		ch[r+1]-=e;
		if(e==s) continue;
		int gc=(e-s)/(r-l);
		cha[l+1]+=gc;
		cha[r+1]-=gc;
	}
	for(int i=1;i<=n;i++){
		cha[i]+=cha[i-1];
		ch[i]+=ch[i-1]+cha[i];
	}
	int maxx=0,an=0;
	for(int i=1;i<=n;i++){
		maxx=max(maxx,ch[i]);
		an^=ch[i];
	}
	cout<<an<<' '<<maxx<<'\n';
	return 0;
}

加强版：Curious Array
注意组合数的性质

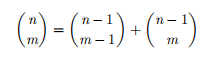
变形一下

发现正好符合差分的形式

每次差分都会有2个单点修改，区间加组合数，且k会减一

k阶差分最后变成对k个差分数组前缀和计算答案

T4 楼房重建

反复递归

T5 [JSOI2009] 计数问题

树状数组秒了

考虑k<=1e9的情况

考虑维护n行的前缀和

单点修改最多影响两个权值前缀和，暴力修改

查询 O(1)前缀和计算答案

需要离散化

#include<iostream>
#include<cstdio>
#include<cstdlib>
#include<cstring>
#include<cmath>
#include<algorithm>
#include<iomanip>
#include<bits/stdc++.h>
#define int long long
#define jiaa(a,b) {a+=b;if(a>=MOD) a-=MOD;}
#define jian(a,b) {a-=b;if(a<0) a+=MOD;}
using namespace std;
int ksm(int a,int b,int p){
	if(b==0) return 1;
	if(b==1) return a%p;
	int c=ksm(a,b/2,p);
	c=c*c%p;
	if(b%2==1) c=c*a%p;
	return c%p;	
}
inline int read()
{
	int x=0,f=1;char ch=getchar();
	while (ch<'0'||ch>'9'){if (ch=='-') f=-1;ch=getchar();}
	while (ch>='0'&&ch<='9'){x=x*10+ch-48;ch=getchar();}
	return x*f;
}
#define lowbit(x) x&(-x)
const int MAXN=305;
int a[305][305],sum[305][305][105];
void modd(int x,int y,int k,int val){
	for(int i=x;i<=MAXN;i+=lowbit(i)){
		for(int j=y;j<=MAXN;j+=lowbit(j)){
			sum[i][j][k]+=val;
		}	
	}
}
int query(int x,int y,int k){
	int ans=0;
	for(int i=x;i;i-=lowbit(i)){
		for(int j=y;j;j-=lowbit(j)){
			ans+=sum[i][j][k];
		}	
	}
	return ans;
}
signed main()
{
	//freopen("filename.in", "r", stdin);
	//freopen("filename.out", "w", stdout);
	int n=read(),m=read();
	for(int i=1;i<=n;i++){
		for(int j=1;j<=m;j++){
			a[i][j]=read();
			modd(i,j,a[i][j],1);
		}
	}
	int q=read();
	while(q--){
		int opt=read();
		if(opt==1){
			int x=read(),y=read(),c=read();
			modd(x,y,a[x][y],-1);
			modd(x,y,c,1);
			a[x][y]=c;
		}
		else{
			int x=read(),xx=read(),y=read(),yy=read();
			int c=read();
			int an=query(xx,yy,c)-query(xx,y-1,c)-query(x-1,yy,c)+query(x-1,y-1,c);
			cout<<an<<'\n';
		}
	}
	return 0;
}

T6 [SHOI2014] 三叉神经树

考虑会让父亲节点权值改变的情况

最后发现改变的是一条链

树链剖分

线段树维护儿子节点和

二分查找一段合法后缀

T7 [十二省联考 2019] 异或粽子

预处理前缀异或和

01trie维护前缀数组与每个元素异或的第j大值

每次取最大放入堆中即可

加强: Friends

二分k大异或值

计算贡献

T8 GSS2 - Can you answer these queries II

先考虑m=1

扫描线

线段树维护区间max,区间和

再考虑多次询问

将问题转化成历史信息最值

转化成矩阵广义乘法

T9 [NOIP2022] 比赛

还是考虑m=1

依旧扫描线

维护线段树，单调栈

多次询问

考虑线段树

同样历史询问信息

转成矩阵乘法

T10 [Code+#1] Yazid 的新生舞会

设S(m,i)表示i之前m有多少个数

题目限制变成：S(r)-S(l-1)>(r-l+1)-S(r)+S(l-1)

移项变成2S(r)-r>2S(l-1)-(l-1)

发现形式一致

设F(r)=2S(r)-r

计算贡献

发现对于区间x,y，贡献每次是x,x+1,x+2,……,y

相当于区间加等差数列

对于>y的部分相当于区间加

查询每次对应区间答案即可