pyyzDay8
大炮2
T1 Centroids
先对一个点进行考虑
若一个点不是树的重心
最多有一个子树>=n/2
所以要在这个子树内删一个<=n/2的siz最大的子树
dp转移即可
问题是现在不定根
如何换根
另记一个子树外<=n/2的siz最大的子树
进行换根
T2 Road Improvement
换根DP时记录0的个数
或者维护前缀和后缀
T3 Adam and Tree
考虑dp记录答案
每次询问时暴力向上修改链的答案
但这是O(N^2)的
考虑优化
若跳到某个点,值没有更新,则就结束更新
这样就是对的
为什么?
考虑树剖,fi的和<=nlogn
我们的答案一定<=树剖的答案
即时间复杂度一定<=O(nlogn)
#include<iostream>
#include<cstdio>
#include<cstdlib>
#include<cstring>
#include<cmath>
#include<algorithm>
#include<iomanip>
#include<bits/stdc++.h>
#define int long long
#define jiaa(a,b) {a+=b;if(a>=MOD) a-=MOD;}
#define jian(a,b) {a-=b;if(a<0) a+=MOD;}
using namespace std;
int ksm(int a,int b,int p){
if(b==0) return 1;
if(b==1) return a%p;
int c=ksm(a,b/2,p);
c=c*c%p;
if(b%2==1) c=c*a%p;
return c%p;
}
inline int read()
{
int x=0,f=1;char ch=getchar();
while (ch<'0'||ch>'9'){if (ch=='-') f=-1;ch=getchar();}
while (ch>='0'&&ch<='9'){x=x*10+ch-48;ch=getchar();}
return x*f;
}
int fa[1000005],maxx[1000005],sec[1000005],dp[1000005];
bool dfs(int x){
int ff=fa[x];
if(dp[x]>maxx[ff]){
sec[ff]=maxx[ff];
maxx[ff]=dp[x];
}
else if(dp[x]>sec[ff]){
sec[ff]=dp[x];
}
int ans=max(maxx[ff],sec[ff]+1);
if(ans==dp[ff]) return 0;
dp[ff]=ans;
return 1;
}
signed main()
{
//freopen("filename.in", "r", stdin);
//freopen("filename.out", "w", stdout);
int n=read();
fa[1]=0;
dp[1]=1;
for(int i=1;i<=n;i++){
fa[i+1]=read();
int j=i+1;
dp[j]=1;
while(fa[j]){
if(!dfs(j)) break;
j=fa[j];
}
cout<<maxx[1]<<'\n';
}
return 0;
}
T4 [USACO23FEB] Watching Cowflix P
考虑暴力DP
设 fi,0/1 表示 i 为根的子树,i 现在不在/在连通块内的最小代价
其中关键点必须在连通块里
转移时考虑节点u是否选
发现若两个联通块之间的点的个数<=k,则合并不劣
于是发现联通快个数m<=n/k
若k<=sqrt(n),直接暴力
否则,块个数<=sqrt(n)
设dpi,j,0/1表示 i 为根的子树,分成 j 个连通块,其中 i 不在/在连通块里的最小代价
转移是树上背包
T5 [IOI 2014] friend 朋友
分情况
设fi,0/1表示i等效于选or不选
case1:没有上司的舞会
case2:发现这种情况i点和fa_i的影响是一样的
故 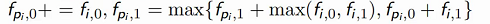
case3:发现这只是将1~2情况合并
#include<bits/stdc++.h>
using namespace std;
int dp[100005][2];
int findSample(int n, int confidence[], int host[], int protocol[]){
for(int i=0;i<n;i++) dp[i][1]=confidence[i];
for(int i=n-1;i;i--){
if(!protocol[i]){
dp[host[i]][0]+=max(dp[i][0],dp[i][1]);
dp[host[i]][1]+=dp[i][0];
}
else if(protocol[i]==1){
dp[host[i]][1]=max(dp[host[i]][1]+max(dp[i][0],dp[i][1]),dp[host[i]][0]+max(dp[i][0],dp[i][1]));
dp[host[i]][0]+=dp[i][0];
}
else{
dp[host[i]][1]=max(dp[host[i]][1]+dp[i][0],dp[host[i]][0]+max(dp[i][0],dp[i][1]));
dp[host[i]][0]+=dp[i][0];
}
}
return max(dp[0][0],dp[0][1]);
}
T6 [ARC171D] Rolling Hash
考虑hash的本质
枚举子集 O(n^3)
#include<iostream>
#include<cstdio>
#include<cstdlib>
#include<cstring>
#include<cmath>
#include<algorithm>
#include<iomanip>
#include<bits/stdc++.h>
#define int long long
#define jiaa(a,b) {a+=b;if(a>=MOD) a-=MOD;}
#define jian(a,b) {a-=b;if(a<0) a+=MOD;}
using namespace std;
int ksm(int a,int b,int p){
if(b==0) return 1;
if(b==1) return a%p;
int c=ksm(a,b/2,p);
c=c*c%p;
if(b%2==1) c=c*a%p;
return c%p;
}
inline int read()
{
int x=0,f=1;char ch=getchar();
while (ch<'0'||ch>'9'){if (ch=='-') f=-1;ch=getchar();}
while (ch>='0'&&ch<='9'){x=x*10+ch-48;ch=getchar();}
return x*f;
}
int tu[20][20],f[1000005],dp[1000005];
signed main()
{
//freopen("filename.in", "r", stdin);
//freopen("filename.out", "w", stdout);
int P=read(),b=read(),n=read(),m=read();
for(int i=1;i<=m;i++){
int l=read(),r=read();
tu[l-1][r]=tu[r][l-1]=1;
}
if(P>=n){
cout<<"Yes"<<'\n';
return 0;
}
for(int i=0;i<(1<<(n+1));i++){
f[i]=1;
for(int u=0;u<=n;u++){
if(i>>u&1){
for(int v=u+1;v<=n;v++){
if((i>>v&1)&&tu[u][v]){
f[i]=0;
break;
}
}
if(!f[i]) break;
}
}
}
memset(dp,0x3f,sizeof(dp));
dp[0]=0;
for(int i=1;i<(1<<(n+1));i++){
for(int t=i;t;t=(t-1)&i){
if(f[t]) dp[i]=min(dp[i],dp[t^i]+1);
}
}
if(dp[(1<<(n+1))-1]<=P) cout<<"Yes"<<'\n';
else cout<<"No"<<'\n';
return 0;
}
T7 [省选联考 2021 A/B 卷] 滚榜
考虑暴力状压
设 fS,i,j,k 表示前 |S| 个位置放了集合 S,上一个放的 i,上一个 b 为 j,之前 b 总和为 k 的方案数
但复杂度爆炸
考虑将b筛掉
发现原来限制是:
bi+1>=bi
b_i+1 + a_i+1>=bi + ai
将其移项
变成 b_i+1 - bi >=0
b_i+1 - bi + a_i+1>=ai
发现记录差分数组即可删掉b这一维
于是设 fS,i,j 表示集合 S 已经放入,上一个放的 i,前面的 b 和这些 b 对后面的影响一共占用了 j 的方案数
转移即可
T8 [NOI2015] 寿司晚宴
因为一个数大于根号的质因子最多只有一个
故对质因子进行状压
若k<sqrt(n)直接DP给二人或都不给
否则将大质数的倍数全部只能给某一个人
复杂度 O(3^k*n),其中 k 是取的小质数数量,这里为 8
T9 [NOIP 2017 提高组] 宝藏
树形DP/按层DP + 状压DP
#include<bits/stdc++.h>
using namespace std;
#define int long long
const int maxn=5005;
int f[maxn][20][20];
int tu[20][20];
int n,m;
signed main(){
ios::sync_with_stdio(0);
cin.tie(0), cout.tie(0);
cin>>n>>m;
for(int i=0;i<n;i++){
for(int j=0;j<n;j++){
tu[i][j]=1000000000;
}
}
for(int S=0;S<maxn;S++){
for(int i=0;i<n;i++){
for(int j=1;j<=n+1;j++){
f[S][i][j]=1000000000;
}
}
}
for(int i=1;i<=m;i++){
int u,v,w;
cin>>u>>v>>w;
tu[u-1][v-1]=tu[v-1][u-1]=min(tu[u-1][v-1],w);
}
for(int i=0;i<n;i++){
for(int j=1;j<=n;j++){
f[1<<i][i][j]=0;
}
}
for(int S=0;S<(1<<n);S++){
for(int i=0;i<n;i++){
if(!((S>>i)&1)) continue;
for(int j=1;j<=n;j++){
for(int k=0;k<n;k++){
for(int T=S;T;T=(T-1)&S){
if(!((T>>k&1))) continue;
f[S][i][j]=min(f[S][i][j],f[S^T][i][j]+f[T][k][j+1]+tu[i][k]*j);
}
}
}
}
}
int ans=1000000000;
for(int i=0;i<n;i++){
for(int j=1;j<=n;j++){
ans=min(ans,f[(1<<n)-1][i][j]);
}
}
cout<<ans<<'\n';
return 0;
}
T10 [JLOI2015] 管道连接
最小斯坦纳树
考虑对最小斯坦纳树再进行状压



 浙公网安备 33010602011771号
浙公网安备 33010602011771号