刷题技巧

二分

1.求第k大（配合双指针）

2.求中位数（赋值01）

3.01分数规划

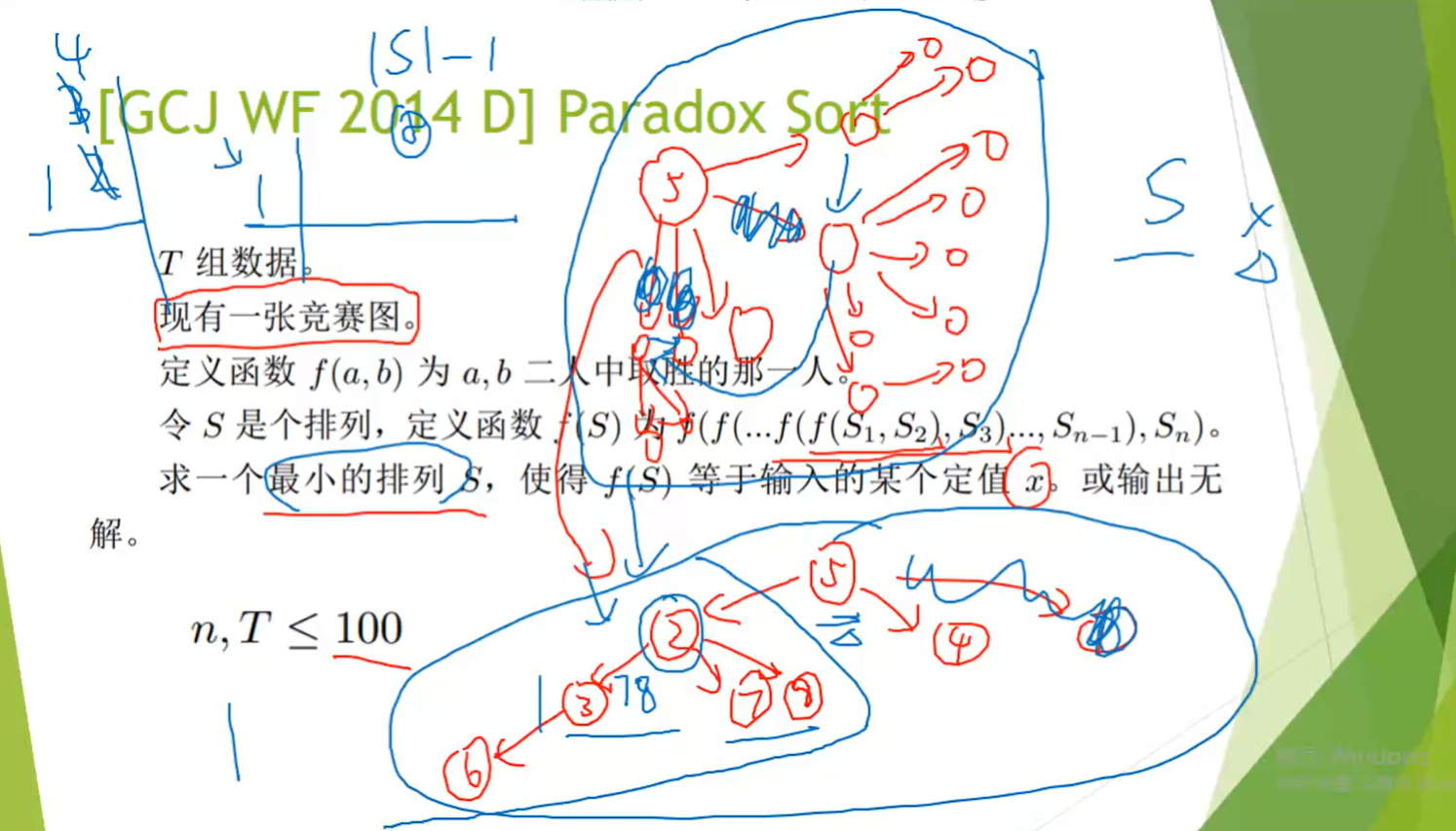
例：在一个有向图上求一个环使得平均边权最大

二分答案y，将每个边权-y

问题变成是否存在正环

SPFA判负环即可

哈希

尽量写双模哈希

例题：小C找朋友

发现对于任意两个小C i，j，当且仅当其对应每个点的连边关系相同，两人才符合要求

首先考虑O(n^2)做法

将图的关系建成链接矩阵

对于任意两个小C i，j，若其对应的那一行链接矩阵相同，则符合要求

考虑优化

进行邻接表存图

每个点都有一个连边关系的字符串

进行hash找重复的数量即可

例2：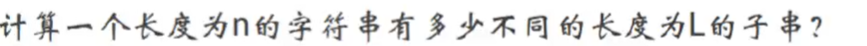

首先考虑O(n^2)

对于每一个子串进行考虑，双模哈希，判断是否符合条件（别忘了长度的限制）

优化：

考虑由于长度一定，用类似滑动窗口的做法

用进制hash可以快速在一个子串插入、删除

如： abbbca,L=3,base=114

当枚举到bbc时，其hash值为b114^2+b114+c

当右移至bca时，其hash值为b114^2+c114+a

发现只需先将首项去掉变成b*114+c

然后乘base114变成b114^2+c114

最后加a

这样O(n)枚举了所有长度为L的子串

双模hash即可

例3：

数学

注意求和区间不变

对于给定的i，修改不影响答案的数的位置

最后的容斥可以进行小爆搜（质因数本来就很少，爆搜复杂度顶多40）

不过学过莫反的人容易发现系数其实就是莫比乌斯系数

直接判断正负即可

双指针

构造

例1：

(题目是CF306D Polygon)

考虑无需环

故选择任意一棵生成树

将每个节点与其父亲的运输水量关系记录（记录谁向谁输多少水，可以树形DP）

然后从叶子结点开始运输

发现每条边最多运输2次，最多n个叶子，故最多2n^2次运输

也可根据每条边的水量进行贪心，从大往小运输（缺点是不好证明运输次数）

例2：

注：要求完全图

可以自己试着构造一下，发现有且只有n=4不行

于是分奇偶讨论

发现当n个点成立时，新增n+1,n+2

将n+2->n+1;

n+1->1,2,3……n;

1,2,3……n->n+2;

即可解决所有的情况

（新增点的另法：
）

于是构造出n=3/n=6即可

n=3构成环即可

n=6时构造如下：（不全）

例3:

CF333C Lucky Tickets

如果在 8 个数字间加入一些运算符和括号，使这个表达式的值为 k，则称这样 8 个数字为 k-幸运数字串。给出 k,m，请构造 m 个 k-幸运数字串。

例4：

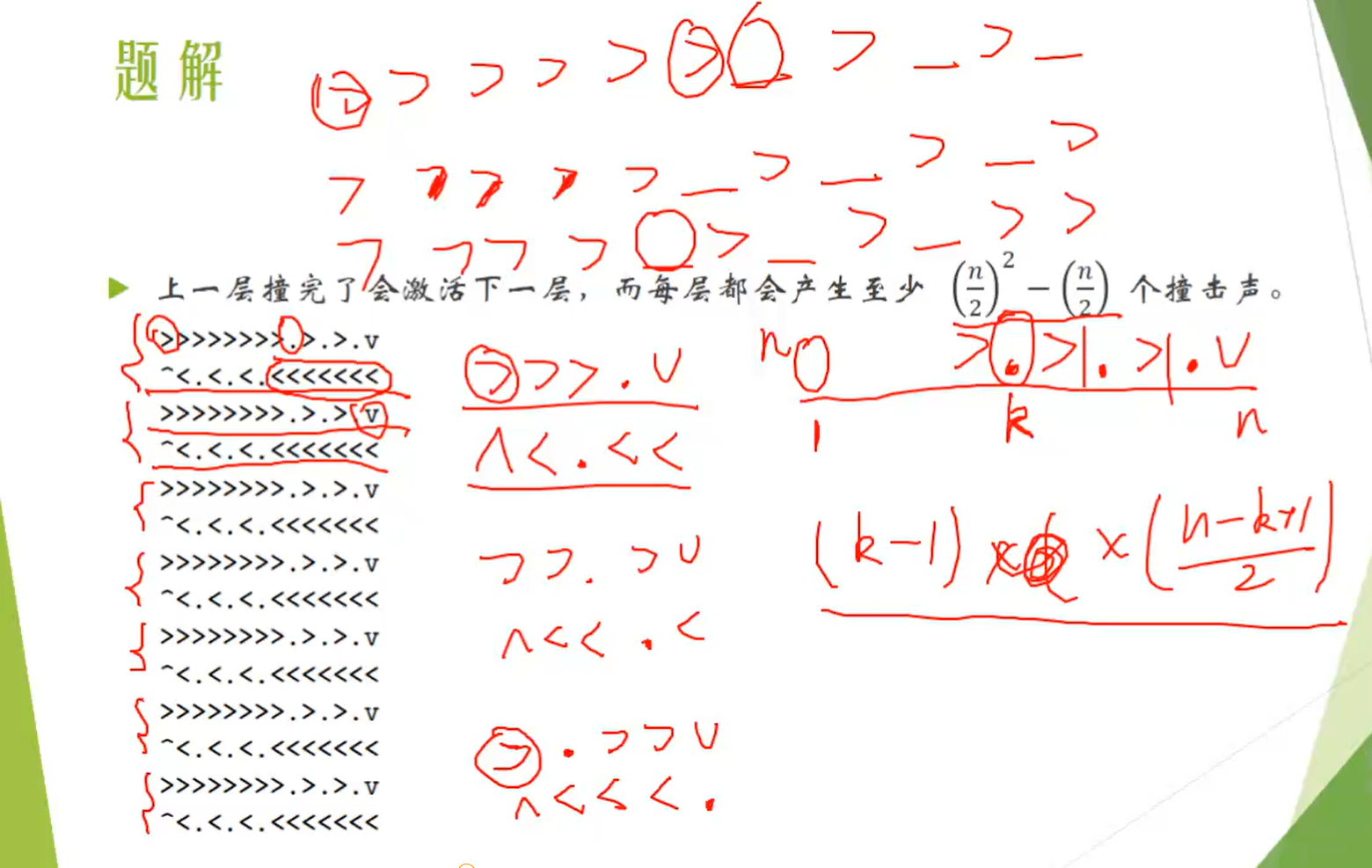
最后解得k大约是n/2-1

例5：

Paradox sort

构造小技巧：倒着考虑

有趣的T

1.

值域分块！

对每个值域块内，可以再开数组记录每个数出现次数

2.

sub1:单调栈

sub2:

3.

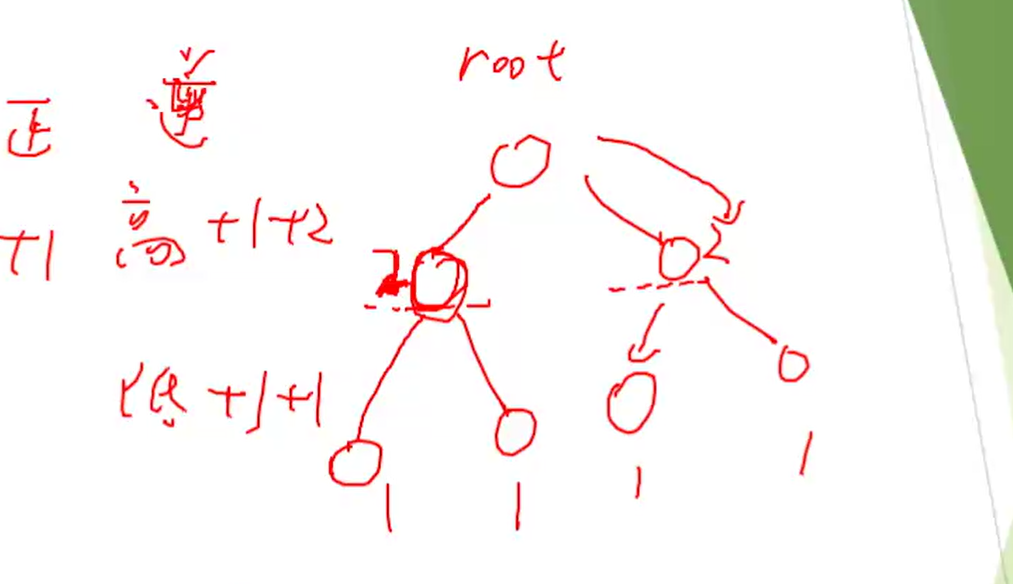
二进制下从高位往低位贪心

若第i位顺序对个数<逆序对个数，则第i位为1

如何统计逆序对个数？

01trie维护不同层数的点的个数

然后快速判断每一层逆序对个数

如：3 1 2 0

4.

发现P无关

可对调的数一定是序列的某个前缀和某个后缀

且他们的和相同

统计即可

O(nlogn):找合法方案时记录一个map/set，反复进行查找，把复杂度降至O(nlogn)

对调时，双指针，记录一个map，查询前缀与后缀相等的个数

5.

6.

7.

一棵DFS树是可以将根节点的儿子变成只有一个（因为没有横叉边）

所以可以将一棵DFS树变成一条链（因为强联通，所以有环）

哈密顿回路指的是在一个图中经过每个顶点恰好一次并最终回到起点的闭合路径

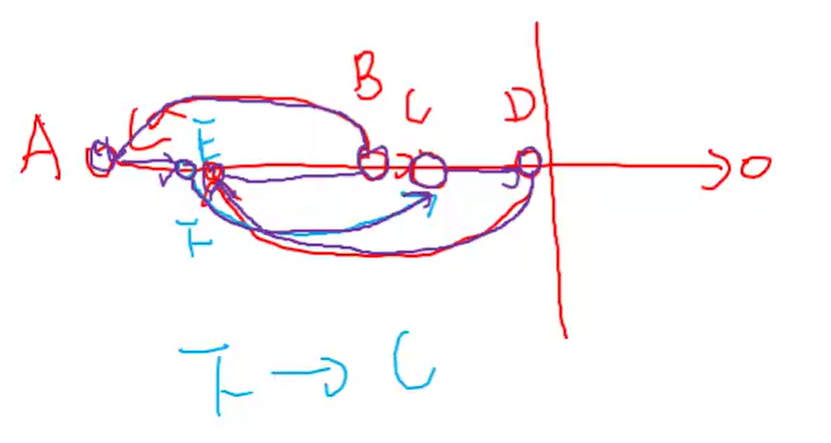
如图，AB是已知简单环，C是B+1，D是从C往后第一个能连向AB之间的点

E是D连向AB之间的点，F是E-1

因为D是第一个能连向AB之间的点，所以一定是F->C

所以存在一条合法简单环：F->C->D->E->B->A->F

8.

考虑到允许重边

故横着匹配的方案数为边数的乘积，斜着匹配的方案数始终为1

因为3^20>1e9

所以每个点的横着连边3条，对K进行三进制拆分

故如下构造：

9.