图论-最短路

图论基本概念

迹：不经过重复边

回路：不经过重复边且起点与终点相同

路径：不经过重复点

环：不经过重复点且起点与终点相同

易发现路径一定是迹，环一定是回路

最短路

只考虑路径，且无负环

Bellman-Ford

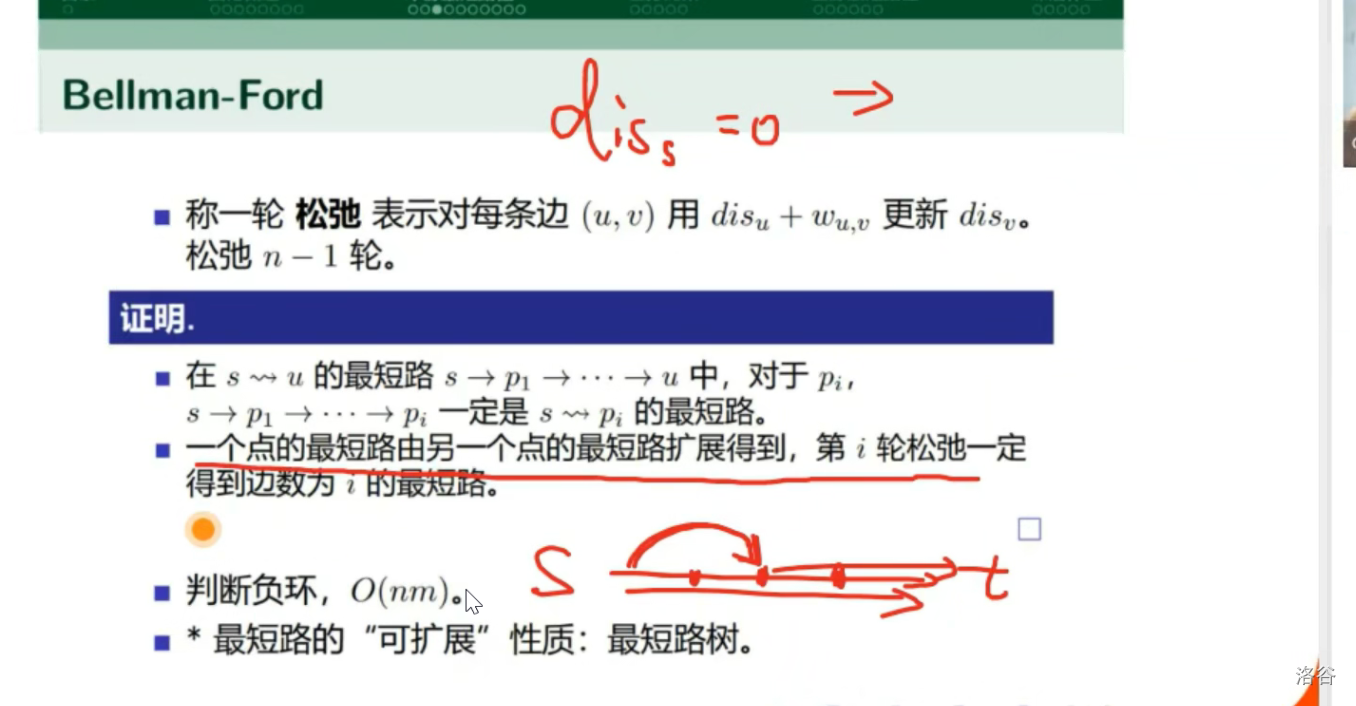
可扩展性质：最短路树

SPFA

注意：使用SPFA时求点对点的最短路径（费用流），队头为目标节点时不能结束算法

Dijkstra

求第k小即为前k个更新的

值域小：开桶

例题：

通往奥格瑞玛的道路

二分+dij

[GXOI/GZOI2019] 旅行者

查分约束

例题：
赛车游戏

固定起点是1，设从1到n的最短路为Du

将边权限制转化为路径限制

已知Dv-Du=Wu,v

而且1<=Wu,v<=9

那么1<=Dv-Du<=9

查分约束

注意特判从1到不了n的情况和有环的情况

AT_agc056_c [AGC056C] 01 Balanced

很巧妙的题

将0看成1,1看成-1

S前缀和满足

Sr=S(l-1)

abs(Si-S(i-1))=1

但是abs(Si-S(i-1))=1我们没法做

所以感性理解一下，发现如果要求abs(Si-S(i-1))<=1,跑查分约束也是最优解

所以就可以将Sr=S(l-1) ，abs(Si-S(i-1))<=1跑差分约束即可

Floyd

注意k的枚举顺序不重要

例题：

心跳最短路

n次扣掉一个点求全源最短路

缺一分治思想

每次递归分治，将另一半全部加入

由于Floyd中转点可以任意枚举，所以这个做法正确

传递闭包

快速求两点之间是否可达

Johnson

n遍SPFA变成n遍Dij（强制将边权变为正数）

例题：

AT_abc232_g [ABC232G] Modulo Shortest Path

对模数进行操作

先建立一个长为m的环

对于一个i，将Bi->i连边,i->-Ai连边

对多余的环上的点进行缩点

跑最短路即可