八皇后问题

八皇后问题

众所周知，八皇后问题，就是给你一个8*8的棋盘，你有8个皇后棋子，如何摆放棋子，使得他们不互相攻击，也就是说，如何摆放，使得任意两个棋子不在同一行，不在同一列，也不在同一个对角线。已经知道，有92种摆法。

思路解析

这是一道经典的回溯问题，很容易想到，我们可以搜索每一个位置，如果这个位置合适了，就把棋子放上去，那么如何确定合适位置？可以一行一行看。

首先看第一行，这时我们要摆放第一个棋子，这个棋子是没有限制的，它可以放在第一行的任意一列，那我们就可以一个一个试，假设放在了第一列。当我们在第二行放第二个棋子的时候，我们就要考虑了，因为此时棋盘上已经有了一个棋子了，如果我们也放在第一列，显然不合适（此时两个棋子在同一列，不符合要求），

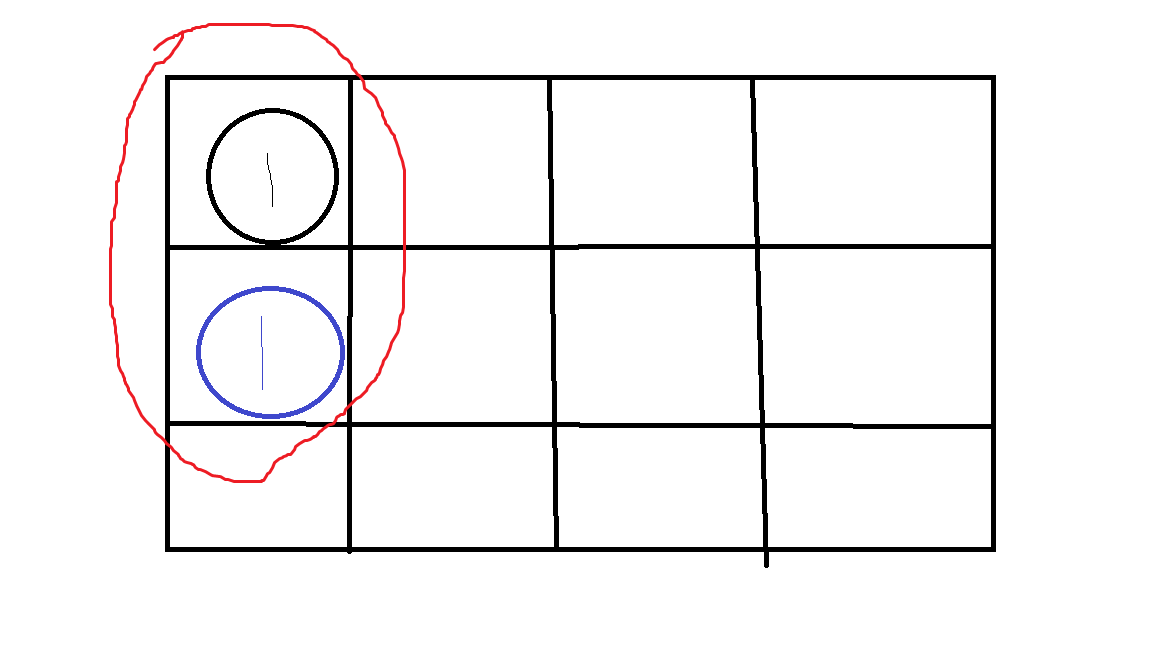
如果放在第二列，也不可以（两个棋子在同一对角线，也不符合要求），

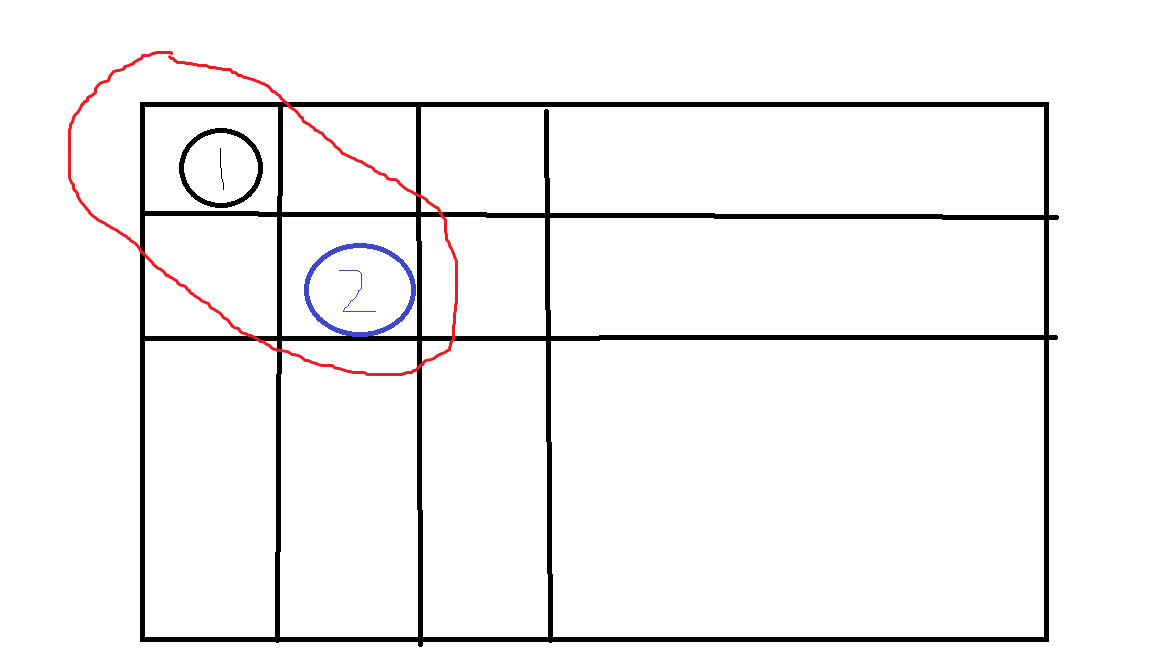
如果放在第三列，这个时候，就没有问题了，这是个合适的位置。

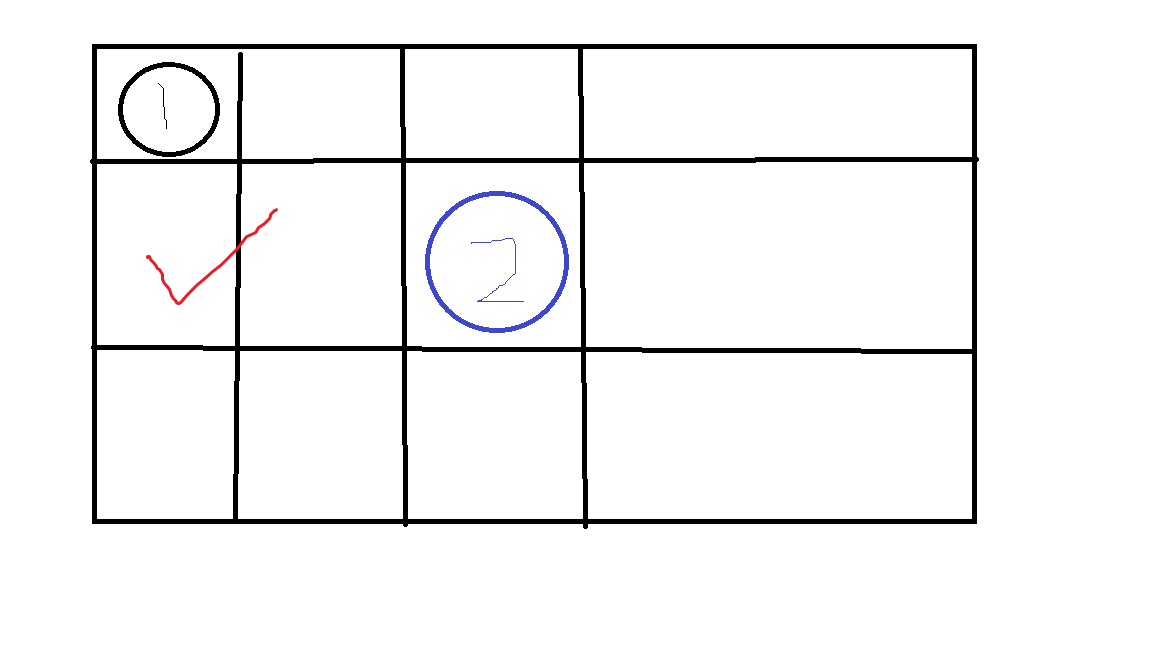
以此类推，我们每放一个棋子，只要符合上面三个要求，这个位置就可以放（不需要考虑行了，因为我们本来就是一行放一个）。那么我们可以建几个数组col[]，left[]，right[]，分别表示列，左对角，右对角，初始值为0，如果这列，或者这个左（右）对角已经有皇后了，就标为1，每准备放一个棋子，就在这几个数组里判断一下。

难点分析

其实col数组很好表示，棋子在i列放置，那就是col[I] = 1即可，对于left right可能要麻烦一点，通过找规律可以发现：

 

 

 

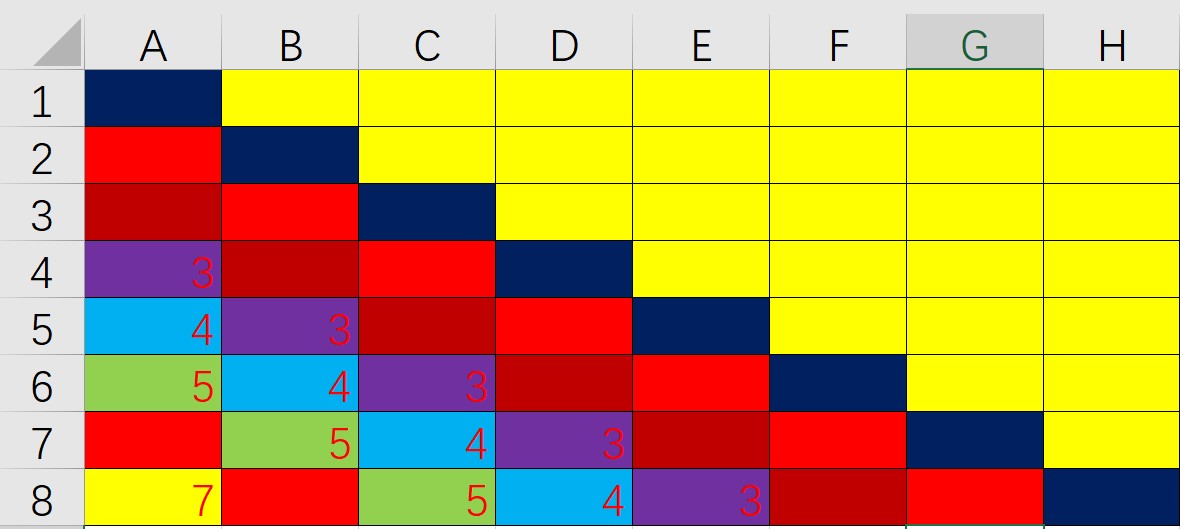
（这是一个8*8的表格，模拟棋盘，图中不同颜色代表不同的左对角线，共有15条左对角线）可以发现，每一个处在同一个左对角线的单元格的行坐标-列坐标的差值是固定的，图中数字表明了一些对角线的差值，有些差值为负数，为了符合c++数组下标的规范，我们把每个差值都加上7（最小差值为-7，这也是加上7的理由），这样就可以用下标来表示每一个左对角线。右对角线也有规律，同一个右对角线的单元格的行列坐标和相同，同样我们把每个和-2，为了满足数组下标。这样，我们就可以用这些数组来表示，列，对角线了。

完整代码

 

#include <stdio.h>
#include <iostream>
#include <cstring>
using namespace std;
int cnt = 0; //方便输出用的计数器
int a[9];   // 用一维数组来记录每一行的皇后排列情况，节省空间 （虽然我感觉也没节省多少）
int Left[15]; // 左对角线，记录某条对角线上是否有皇后
int Right[15]; // 右对角线 同上
int col[9];  // 列数组，记录某列是否有皇后
void eight(int line)
{
    if(line == 9)  // 注意，此处应该是9，不能是8，因为第8行也要有皇后
    {
        // 此处是打印结果，可以跳过
        printf("----Case %d----\n",++cnt);
        for(int i = 1; i <= 8; i++)
        {
            for(int j = 1; j <= 8; j++)
            {
                if(j == a[i]) printf("  @");
                else printf("  #");
            }
            cout << endl;
        }
        cout << endl;
        return;
    }
    if(line == 1)  // 如果是第一行，皇后可以随便放，循环遍历每个位置
    {
        for(int i = 1; i <= 8; i++)
        {
            a[1] = i;     // 为列数组，左数组，右数组做标记
            col[i] = 1;
            Left[8-i] = 1;
            Right[i-1] = 1;
            // 进行递归搜索
            eight(line+1);
            // 注意，回溯回来，一定要标记清零，数组归位
            Left[8-i] = 0;
            Right[i-1] = 0;
            col[i] = 0;
        }
    } else {  // 如果不是第一行，则遍历每一行，寻找合适位置
        for(int i = 1; i <= 8; i++)
        {   // 如果该列，左对角线，右对角线，都没有皇后，则该位置可以放置皇后
            if(col[i] == 0 && Left[line-i+7] == 0 && Right[line+i-2] == 0)
            {
                // 操作同上，依然注意，回溯回来，数组归位
                a[line] = i;
                col[i] = 1;
                Left[line-i+7] = 1;
                Right[line+i-2] = 1;
                eight(line+1);
                col[i] = 0;
                Left[line-i+7] = 0;
                Right[line+i-2] = 0;
            }
        }
    }
}
int main()
{
    // 四个memset可能是多此一举，有备无患吧
    memset(a,0,sizeof(a));
    memset(col,0,sizeof(col));
    memset(Right,0,sizeof(Right));
    memset(Left,0,sizeof(Left));
    eight(1); // 从第一行开始搜索
    return 0;
}