剑指offer 学习笔记 二叉搜索树与双向链表

面试题36：二叉搜索树与双向链表。输入一棵二叉搜索树，将该二叉树转换成一个排序的双向链表。要求不能创建任何新节点，只能调整树中节点指针的指向。

二叉树中，每个节点都有两个指向子节点的指针，双向链表中，每个节点也有两个指针，分别指向前一个节点和后一个节点。在二叉搜索树中，所有左子节点的值总是小于父节点的值，所有右子节点的值总是大于父节点的值，且左右子树都是一棵二叉搜索树，因此，我们在将二叉搜索树转换成排序双向链表时，原先指向左（右）节点的指针调整为链表中指向前（后）一个节点的指针。

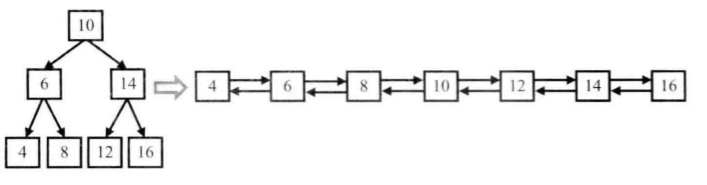
由于要求转换后的链表是排好序的，我们可以中序遍历树中每个节点，中序遍历算法可以按节点元素值从小到大的顺序遍历二叉搜索树。当遍历到根节点时，根节点应该和左子树的最大节点相连，并且和右子树的最小节点相连。当我们遍历到根节点时，它的左子树已经转换为一个排序的链表了，并且处在左子树的排序链表的最后一个节点是左子树中值最大的节点，右子树同理，右子树最小节点是排序链表的首节点，以下代码中以下图树为例：

#include <iostream>
using namespace std;

struct BinaryTreeNode{
    int m_nValue;
    BinaryTreeNode* m_pLeft;
    BinaryTreeNode* m_pRight;
};

void PrintFromSmallToBig(BinaryTreeNode* pStart) {
    while (pStart) {
        cout << pStart->m_nValue << endl;
        pStart = pStart->m_pRight;
    }
}

void PrintFromBigToSmall(BinaryTreeNode* pStart) {
    while (pStart) {
        cout << pStart->m_nValue << endl;
        pStart = pStart->m_pLeft;
    }
}

BinaryTreeNode* ConstructCore(int* startPreorder, int* endPreorder, int* startInorder, int* endInorder) {    // 创建树
    BinaryTreeNode* root = new BinaryTreeNode();
    root->m_nValue = *startPreorder;
    root->m_pLeft = root->m_pRight = nullptr;

    if (startPreorder == endPreorder) {    // 当递归到前序遍历只含一个元素时
        if (startInorder == endInorder && *startPreorder == *startInorder) {    // 此时若中序遍历也只含一个元素并且这个元素值与前序遍历的元素值相同时，递归到底成功返回
            return root;
        } else {    // 否则当前序和中序遍历的个数不相等（前序遍历只含一个元素但中序遍历有多个元素）或值不相等（前序遍历和中序遍历元素数都为1但这两个值不等）时
            throw exception("Invalid input.");    // 说明输入的前序和中序遍历不匹配
        }
    }

    int* rootInorder = startInorder;
    while (rootInorder < endInorder && *rootInorder != *startPreorder) {    // 遍历中序序列找到根节点
        ++rootInorder;
    }

    if (rootInorder == endInorder && *rootInorder != *startPreorder) {    // 若以上循环结束仍未找到根节点，说明输入有误
        throw exception("Invalid input");
    }

    int leftLength = rootInorder - startInorder;    // 左子树长度
    int* leftPreorderEnd = startPreorder + leftLength;    // 左子树尾边界
    if (leftLength > 0) {    // 当左子树仍存在时
        root->m_pLeft = ConstructCore(startPreorder + 1, leftPreorderEnd, startInorder, rootInorder - 1);    // 继续递归左子树
    }
    if (leftLength < endPreorder - startPreorder) {    // 左子树长度小于当前遍历的树节点数-1（去掉根节点）时，说明存在右子树
        root->m_pRight = ConstructCore(startPreorder + leftLength + 1, endPreorder, rootInorder + 1, endInorder);    // 继续递归右子树
    }

    return root;
}

BinaryTreeNode* Construct(int* preorder, int* inorder, int length) {    // 创建树
    if (preorder == nullptr || inorder == nullptr || length <= 0) {
        return nullptr;
    }

    return ConstructCore(preorder, preorder + length - 1, inorder, inorder + length - 1);
}

void ConvertNode(BinaryTreeNode* pNode, BinaryTreeNode** pLastNodeInList) {
    if (pNode == nullptr) {
        return;
    }

    if (pNode->m_pLeft != nullptr) {    // 中序遍历，先找最左子节点
        ConvertNode(pNode->m_pLeft, pLastNodeInList);
    }

    pNode->m_pLeft = *pLastNodeInList;    // 将中序遍历中当前节点与上一节点相连
    if (*pLastNodeInList != nullptr) {    // 上一节点可能为空，若非空时再访问它
        (*pLastNodeInList)->m_pRight = pNode;
    }

    *pLastNodeInList = pNode;    // 更新中序遍历到的节点

    if (pNode->m_pRight != nullptr) {    // 中序遍历，最后找右节点
        ConvertNode(pNode->m_pRight, pLastNodeInList);
    }
}

BinaryTreeNode* Convert(BinaryTreeNode* pRoot) {
    BinaryTreeNode* pLastNodeInList = nullptr;    // 指向当前已经建立的链表的最大元素
    ConvertNode(pRoot, &pLastNodeInList);

    return pLastNodeInList;
}

int main() {
    int preorder[] = { 10,6,4,8,12,14,16 };
    int inorder[] = { 4,6,8,10,12,14,16 };
    BinaryTreeNode *pRoot = Construct(preorder, inorder, 7);
    BinaryTreeNode *pLastNodeInList = Convert(pRoot);
    PrintFromBigToSmall(pLastNodeInList);

    while (pLastNodeInList->m_pLeft != nullptr) {
        pLastNodeInList = pLastNodeInList->m_pLeft;
    }

    cout << "另一个方向打印双向链表：" << endl;
    PrintFromSmallToBig(pLastNodeInList);
}