Floyd算法

Floyd算法适用于APSP(AllPairsShortestPaths)，是一种动态规划算法，稠密图效果最佳，边权可正可负。此算法简单有效，由于三重循环结构紧凑，对于稠密图，效率要高于执行|V|次Dijkstra算法。

优点：容易理解，可以算出任意两个节点之间的最短距离，代码编写简单

缺点：时间复杂度比较高，不适合计算大量数据。

时间复杂度:O(n^3)；空间复杂度:O(n^2)；

任意节点i到j的最短路径两种可能：

1. 直接从i到j；
2. 从i经过若干个节点k到j。

map（i，j）表示节点i到j最短路径的距离，对于每一个节点k，检查map（i，k）+map（k，j）小于map(i，j),如果成立，map（i，j） = map（i，k）+map（k，j）；遍历每个k，每次更新的是除第k行和第k列的数

 

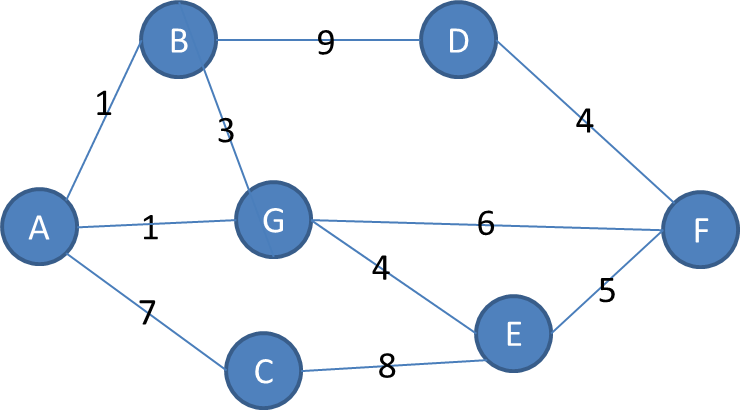
public class FloydTest {

    static char[] vertex = {'A', 'B', 'C', 'D', 'E', 'F', 'G'};
    static int[][] matrix = new int[vertex.length][vertex.length];
    static final int N = 65535;
    static int[][] path = new int[vertex.length][vertex.length];

    public static void main(String[] args) {
        matrix[0] = new int[]{0,1,7,N,N,N,1};
        matrix[1] = new int[]{1,0,N,9,N,N,3};
        matrix[2] = new int[]{7,N,0,N,8,N,N};
        matrix[3] = new int[]{N,9,N,0,N,4,N};
        matrix[4] = new int[]{N,N,8,N,0,5,4};
        matrix[5] = new int[]{N,N,N,4,5,0,6};
        matrix[6] = new int[]{1,3,N,N,4,6,0};
        calculate();
        int start = 0,end = 5;
        System.out.println(vertex[start]+ " - " + vertex[end] + "最短距离："+matrix[start][end]);
        System.out.print("路径："+vertex[start]+",");
        print(0,5);
        System.out.println(vertex[end]);
    }

    public static void calculate(){

        for (int i = 0; i < vertex.length; i++) {
            for (int j = 0; j < vertex.length; j++) {
                path[i][j] = -1;
            }
        }
        for (int i = 0; i < vertex.length; i++) {
            for (int j = 0; j < vertex.length; j++) {
                for (int k = 0; k < vertex.length; k++) {
                    if(matrix[j][i]!=N && matrix[i][k]!=N && j!=k && matrix[j][i]+matrix[i][k]<matrix[j][k]){
                        matrix[j][k] = matrix[j][i]+matrix[i][k];
                        path[j][k] = i;
                    }
                }
            }
        }

    }

    public static void print(int i,int j){
        int k = path[i][j];
        if(k==-1){
            return ;
        }
        print(i,k);
        System.out.print(vertex[k]+",");
        print(k,j);
    }

}