OO第一单元总结

OO第一单元作业小结

一、写在前面：

就算我是一名没接触过java编程的菜鸡，也对oo课程有所耳闻。学长学姐们对于oo课程的描述使我瑟瑟发抖（尤其是评分靠互测）。不过，本次oo课程的改革让我看到了新的希望，引入公测是oo课程的一大进步，圣杯战争也让这门课的互测有娱乐性（甚至有点好玩？反正同质bug可以改）。PS：在此声明我是个好人不是狼（确信）。

说回正题，通过三周以来的学习，能感受到写oo作业给我带来的进步（摧残）的。靠着一本入门的headfirst java，虽然第一次作业是披着面向对象编程的面向输入处理编程，第二次、第三次作业还是很快的掌握了面向对象的使用。（谢谢第二次同屋大佬的代码，让我学会使用了继承和借口hh）尤其是第三次作业，如果使用面向过程编程怕是递归到原地自闭orz。

三周来，感觉自己变秃了，也变强了（并不）

二、基于度量分析程序结构。

第一次作业

第一次作业的流程图如下：

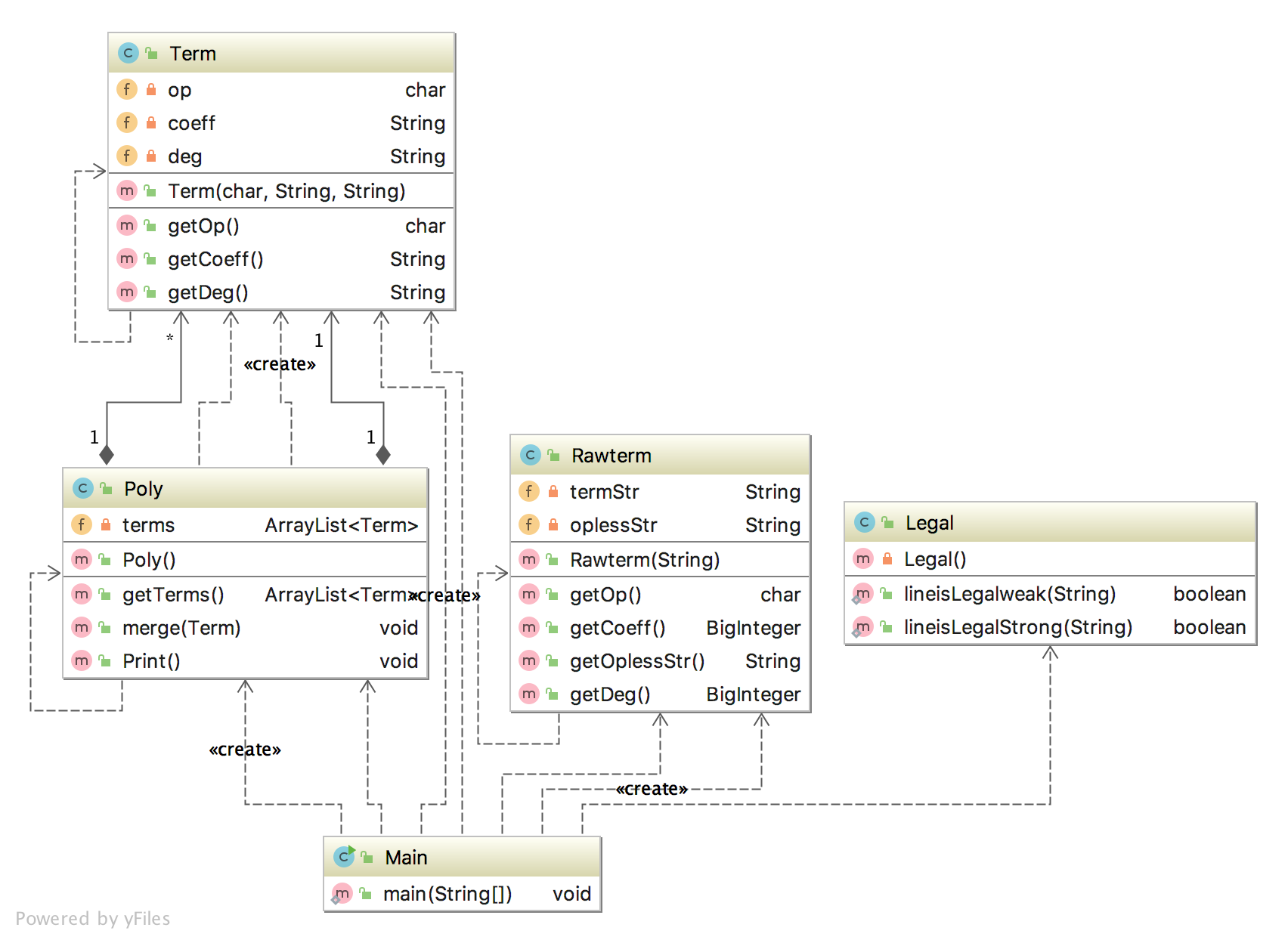
本次作业其实是将Main当作了InputHandler，然后RawTerm和Legal是两个处理函数，Term和Poly是两个简单的类。

第一次作业不甚复杂，随便水水就过了hhh

第二次作业

第二次作业流程图如下：

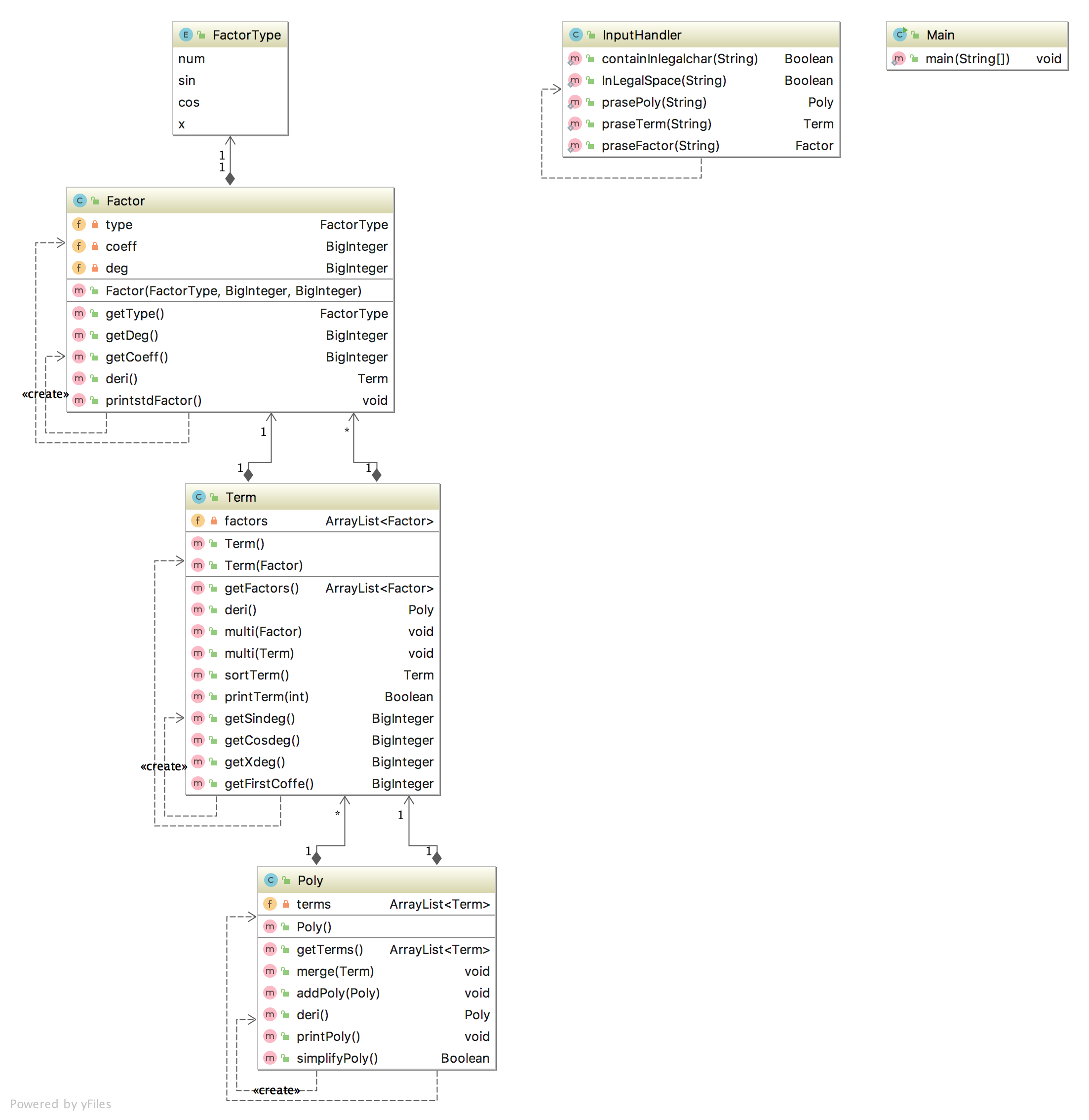
第二次作业有点东西了，考虑到为第三次作业的拓展，一串表达式构造了三个类，Poly、Term、Factor。不过非常可惜的是，由于当时并未熟练掌握继承抽象方法，Factor并没有分出三个子类，而是靠枚举一个FactorType加上if语句（switch语句）来完成不同因子的表示。

printPoly其实就是toString，不过在转化为String的过程中转化一个项就打出来一个。优化由于个人水平有限，没有使用复杂的算法，只是将可以提出sin^2+cos2类别的项进行了一个简单的合并。如果写了toString方法的话，可以通过length来进行判断优化方向的判断，但我当时没想那么多QAQ

感觉写程序之前确实应该多想想，多想十分钟，少改一小时。

第三次作业

第三次作业流程图如下：

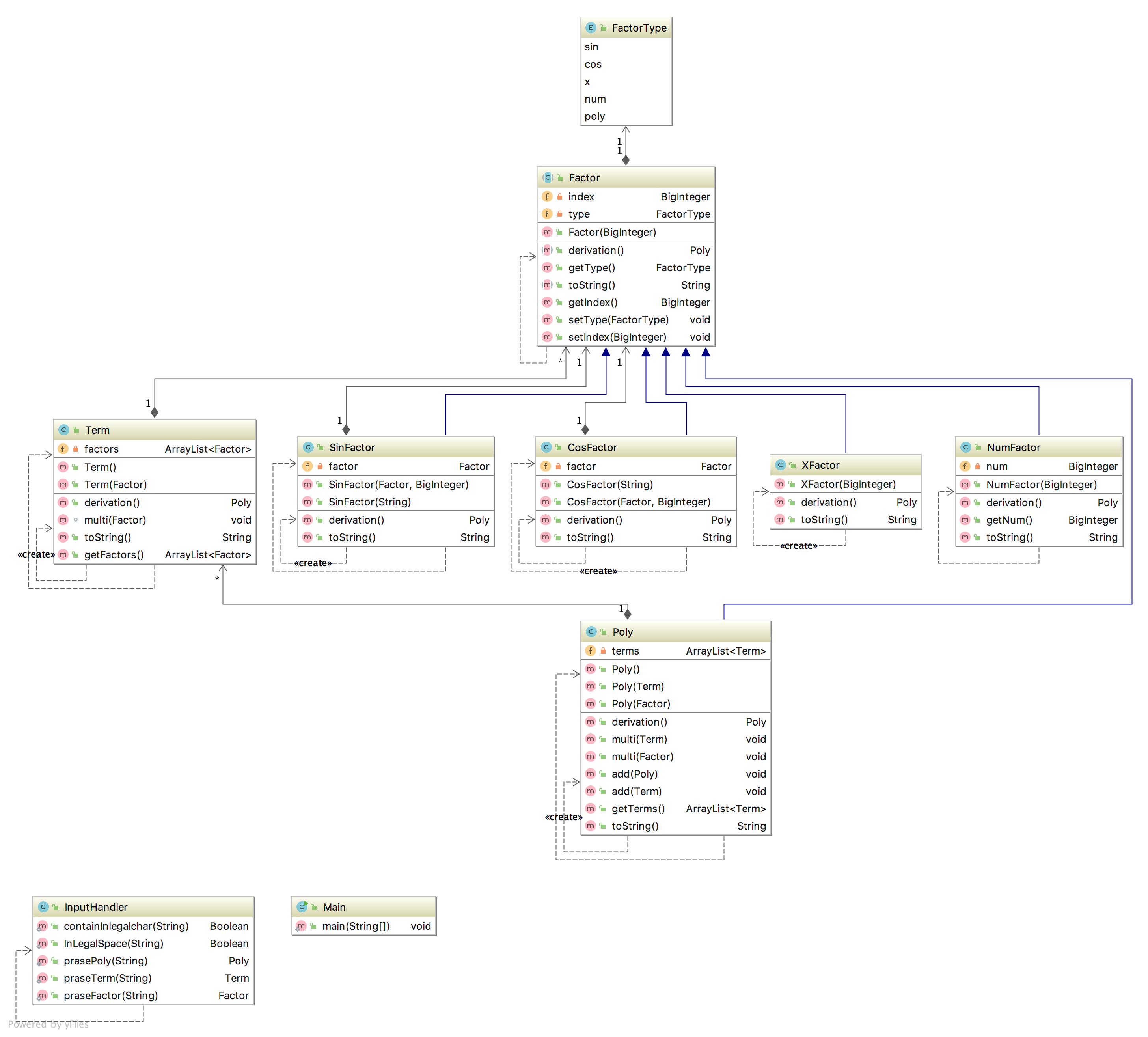
第二次作业其实已经基本把第三次作业的框架写出来了，但是第二次由于没写Factor的子类继承，化简函数写的实在太烦人，不想改了新建了个Project，干脆重构算了。

事实证明重构是对的，重新组织Factor类让我对面向对象有了更深的理解（抽象方法子类继承是真的好用QWQ）。而且第三次作业有第二次的底子，除了写输入函数有一点阻力外，刨去思考时间，写程序花费的时间出奇的少（因为没考虑性能）

至于优化：我得分95.8824,你懂的 ><

度量分析：

由于第一次第二次作业较为简单，在此仅分析第三次作业度量

首先是行数度量

Line number

Source file	Total Line	Source Code Line	Source Code Line %	Comment Line	Comment Line %	Blank Line	Blank Line %
CosFactor.java	68	62	0.9117647058823529	0	0.0	6	0.08823529411764706
Factor.java	30	22	0.7333333333333333	0	0.0	8	0.26666666666666666
FactorType.java	3	3	1.0	0	0.0	0	0.0
InputHandler.java	165	150	0.9090909090909091	6	0.03636363636363636	9	0.05454545454545454
Main.java	29	24	0.8275862068965517	3	0.10344827586206896	2	0.06896551724137931
NumFactor.java	24	18	0.75	0	0.0	6	0.25
Poly.java	87	56	0.6436781609195402	18	0.20689655172413793	13	0.14942528735632185
SinFactor.java	66	61	0.9242424242424242	0	0.0	5	0.07575757575757576
Term.java	80	64	0.8	9	0.1125	7	0.0875
XFactor.java	31	27	0.8709677419354839	0	0.0	4	0.12903225806451613

CosFactor	2.5	10.0
Factor	1.0	5.0
FactorType		0.0
InputHandler	6.4	32.0
Main	3.0	3.0
NumFactor	1.0	4.0
Poly	1.6	16.0
SinFactor	2.5	10.0
Term	2.5	15.0
XFactor	1.6666666666666667	5.0
Total		100.0
Average	2.380952380952381	10.0

Complexity

注：

ev(G)为Essentail Complexity，表示一个方法的结构化程度

iv(G)为Design Complexity，表示一个方法和他所调用的其他方法的紧密程度

v(G)为循环复杂度

OCavg为平均循环复杂度

WMC为总循环复杂度

method	ev(G)	iv(G)	v(G)
InputHandler.praseFactor(String)	9.0	10.0	10.0
Term.multi(Factor)	4.0	4.0	4.0
Term.toString()	3.0	4.0	4.0
InputHandler.praseTerm(String)	3.0	11.0	15.0
InputHandler.containInlegalchar(String)	2.0	1.0	2.0
SinFactor.derivation()	2.0	2.0	2.0
InputHandler.InLegalSpace(String)	2.0	1.0	2.0
CosFactor.derivation()	2.0	2.0	2.0
XFactor.derivation()	2.0	2.0	2.0
Poly.toString()	2.0	2.0	3.0
Term.Term(Factor)	1.0	1.0	1.0
Term.derivation()	1.0	4.0	4.0
Factor.getIndex()	1.0	1.0	1.0
NumFactor.toString()	1.0	1.0	1.0
Poly.getTerms()	1.0	1.0	1.0
Poly.multi(Factor)	1.0	2.0	2.0
Factor.getType()	1.0	1.0	1.0
Poly.multi(Term)	1.0	2.0	2.0
SinFactor.SinFactor(Factor,BigInteger)	1.0	1.0	1.0
Factor.setIndex(BigInteger)	1.0	1.0	1.0
Main.main(String[])	1.0	4.0	4.0
SinFactor.SinFactor(String)	1.0	5.0	5.0
XFactor.XFactor(BigInteger)	1.0	1.0	1.0
NumFactor.NumFactor(BigInteger)	1.0	1.0	1.0
Poly.Poly()	1.0	1.0	1.0
CosFactor.toString()	1.0	2.0	2.0
Poly.derivation()	1.0	2.0	2.0
InputHandler.prasePoly(String)	1.0	5.0	8.0
Poly.add(Term)	1.0	1.0	1.0
CosFactor.CosFactor(Factor,BigInteger)	1.0	1.0	1.0
Poly.Poly(Term)	1.0	1.0	1.0
XFactor.toString()	1.0	2.0	2.0
Factor.Factor(BigInteger)	1.0	1.0	1.0
NumFactor.derivation()	1.0	1.0	1.0
CosFactor.CosFactor(String)	1.0	5.0	5.0
Term.Term()	1.0	1.0	1.0
Term.getFactors()	1.0	1.0	1.0
Poly.Poly(Factor)	1.0	1.0	1.0
NumFactor.getNum()	1.0	1.0	1.0
SinFactor.toString()	1.0	2.0	2.0
Poly.add(Poly)	1.0	2.0	2.0
Factor.setType(FactorType)	1.0	1.0	1.0
Total	63.0	96.0	106.0
Average	1.5	2.2857142857142856	2.5238095238095237

Class	OCavg	WMC
CosFactor	2.5	10.0
Factor	1.0	5.0
FactorType		0.0
InputHandler	6.4	32.0
Main	3.0	3.0
NumFactor	1.0	4.0
Poly	1.6	16.0
SinFactor	2.5	10.0
Term	2.5	15.0
XFactor	1.6666666666666667	5.0
Total		100.0
Average	2.380952380952381	10.0

从本次作业的度量中可以看出，复杂度最高的类和方法都与InputHandler有关（实际上这三次作业最大的难点就是Wrong Format！和输入数据）。因为第三次作业无限嵌套的形式，对于输入的读入只能采用递归配合正则表达式进行读入，再加上一个Factor有5个不同种类，导致InputHandler的复杂度过高QAQ

三、程序BUG分析

三次作业强侧正确性都没有问题。

第一次作业互测中存在对空格位置判断的Bug，少判断了一种带符号整数内的Bug。没有找出其他Bug

互测中第二三次均没有在互测中被测试出Bug，但实际上在后来对自己的测试中测出了某种特定情况的空格判断Bug。

综上，所有Bug都是输入过程中空格导致的Wrong format！果然简单优化/不优化连被找Bug的资格都没有QAQ

四、如何找别人BUG

在第一次作业中，我采用把别人程序下载下来，然后构造各种结构，手动进行Bug测试。

第二次作业中，我使用了自动生成的对拍器，但是同组人过于神仙，一个都没找到。

第三次作业我结合对拍器进行测试，通过观察异样输出找到了3个Bug。

结合三次作业找Bug历程，第一次和第二次的作业因为计算较为简单，Bug均集中在Wrong Format上，第三次作业不让直接使用Wrong Format，因此主要错误集中在输出格式是Wrong Format上hhhh（面向Wrong Format编程实锤了2333）

另外由于我的对拍器只能生成合法数据，根据同组人输出计算结果。。。可是同组人程序算出来的数值都没错orz，要有错也只会是格式错误（比如化简后输出空串）。

五、Applying Creational Pattern

在第三次作业中，为了进行嵌套，我使用了Factor抽象类。枚举了FactorType使之包含三角函数因子、x幂因子、常数因子以及表达式因子。

public enum FactorType {
    sin,cos,x,num,poly;
}

import java.math.BigInteger;

public abstract class Factor {
    private BigInteger index;
    private FactorType type;

    public abstract Poly derivation();

    public FactorType getType() {
        return type;
    }

    public Factor(BigInteger tmp) {
        this.index = tmp;
    }

    public abstract String toString();

    public BigInteger getIndex() {
        return index;
    }

    public void setType(FactorType type) {
        this.type = type;
    }

    public void setIndex(BigInteger index) {
        this.index = index;
    }
}

六、心得体会

好好学习天天向上，每次作业早点开始，早点结束，才能更舒服的摸鱼。

try所有catch Wrong Format确实好用。

多构思十分钟，少删改一小时。干巴爹。