python[4] 函数
函数是什么?
函数一词来源于数学,但编程中的「函数」概念,与数学中的函数是有很大不同的,具体区别,我们后面会讲,编程中的函数在英文中也有很多不同的叫法。在BASIC中叫做subroutine(子过程或子程序),在Pascal中叫做procedure(过程)和function,在C中只有function,在Java里面叫做method。
定义: 函数是指将一组语句的集合通过一个名字(函数名)封装起来,要想执行这个函数,只需调用其函数名即可
特性:
- 减少重复代码
- 使程序变的可扩展
- 使程序变得易维护
语法定义
def sayhi():#函数名 '函数解释' print("Hello, I'm nobody!") sayhi() #调用函数
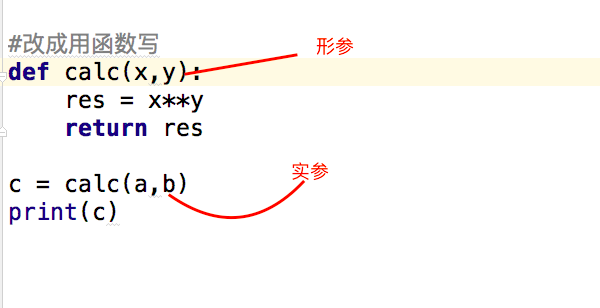
1 #下面这段代码 2 a,b = 5,8 3 c = a**b 4 print(c) 5 6 7 #改成用函数写 8 def calc(x,y): 9 res = x**y 10 return res #返回函数执行结果 11 12 c = calc(a,b) #结果赋值给c变量 13 print(c)
函数参数与局部变量
形参变量只有在被调用时才分配内存单元,在调用结束时,即刻释放所分配的内存单元。因此,形参只在函数内部有效。函数调用结束返回主调用函数后则不能再使用该形参变量
实参可以是常量、变量、表达式、函数等,无论实参是何种类型的量,在进行函数调用时,它们都必须有确定的值,以便把这些值传送给形参。因此应预先用赋值,输入等办法使参数获得确定值
关键参数
正常情况下,给函数传参数要按顺序,不想按顺序就可以用关键参数,只需指定参数名即可,但记住一个要求就是,关键参数必须放在位置参数之后。
非固定参数
若你的函数在定义时不确定用户想传入多少个参数,就可以使用非固定参数
还可以有一个**kwargs
1 def test1(): 2 return 0 3 4 def test2(): 5 return 1,'hello',['name','alex'],{'sex','female'} 6 7 t2 = test2() 8 9 print(t2[2]) 10 11 12 def test3(x,y): 13 print(x) 14 print(y) 15 return x,y 16 17 #两种调用方式 如果混用 关键词参数不能写在位置参数前面 18 test3(1,3) 19 test3(y=1,x=2) 20 test3(1,y=4) 21 22 # 默认参数 23 def test4(x,y=2): 24 print(x) 25 print(y) 26 return 0 27 test4(4) 28 29 # 参数组 args 接收位置参数 参数不固定 会放入元祖中 30 def test5(*x): 31 print(x) 32 return x 33 #传参方式 34 test5(1,2,3,4,5,6) 35 test5(*[1,3,4,5,6]) 36 37 def test6(x,*y): 38 print(x) 39 print(y) 40 return 0 41 42 # **kwargs 接收关键字参数 传入成字典 43 def test7(**kwargs): 44 print(kwargs) 45 return 46 #传参方式 47 test7(name='aaa',sex='f',age=10) 48 test7(**{'name':'bb','age':6})
局部变量
name = "Alex Li" def change_name(name): print("before change:",name) name = "金角大王,一个有Tesla的男人" print("after change", name) change_name(name) print("在外面看看name改了么?",name)
全局与局部变量
返回值
要想获取函数的执行结果,就可以用return语句把结果返回
注意:
- 函数在执行过程中只要遇到return语句,就会停止执行并返回结果,so 也可以理解为 return 语句代表着函数的结束
- 如果未在函数中指定return,那这个函数的返回值为None
嵌套函数
name = "Alex" def change_name(): name = "Alex2" def change_name2(): name = "Alex3" print("第3层打印",name) change_name2() #调用内层函数 print("第2层打印",name) change_name() print("最外层打印",name)
递归
1 def calc(n): 2 print(n) 3 if int(n/2) ==0: 4 return n 5 return calc(int(n/2)) 6 7 calc(10) 8 9 输出: 10 10 11 5 12 2 13 1 14
递归特性:
1. 必须有一个明确的结束条件
2. 每次进入更深一层递归时,问题规模相比上次递归都应有所减少
3. 递归效率不高,递归层次过多会导致栈溢出(在计算机中,函数调用是通过栈(stack)这种数据结构实现的,每当进入一个函数调用,栈就会加一层栈帧,每当函数返回,栈就会减一层栈帧。由于栈的大小不是无限的,所以,递归调用的次数过多,会导致栈溢出)
堆栈扫盲http://www.cnblogs.com/lln7777/archive/2012/03/14/2396164.html
递归函数实际应用案例,二分查找
1 data = [1, 3, 6, 7, 9, 12, 14, 16, 17, 18, 20, 21, 22, 23, 30, 32, 33, 35] 2 3 4 def binary_search(dataset,find_num): 5 print(dataset) 6 7 if len(dataset) >1: 8 mid = int(len(dataset)/2) 9 if dataset[mid] == find_num: #find it 10 print("找到数字",dataset[mid]) 11 elif dataset[mid] > find_num :# 找的数在mid左面 12 print("\033[31;1m找的数在mid[%s]左面\033[0m" % dataset[mid]) 13 return binary_search(dataset[0:mid], find_num) 14 else:# 找的数在mid右面 15 print("\033[32;1m找的数在mid[%s]右面\033[0m" % dataset[mid]) 16 return binary_search(dataset[mid+1:],find_num) 17 else: 18 if dataset[0] == find_num: #find it 19 print("找到数字啦",dataset[0]) 20 else: 21 print("没的分了,要找的数字[%s]不在列表里" % find_num) 22 23 24 binary_search(data,66)
匿名函数
匿名函数就是不需要显式的指定函数
1 #这段代码 2 def calc(n): 3 return n**n 4 print(calc(10)) 5 6 #换成匿名函数 7 calc = lambda n:n**n 8 print(calc(10))
你也许会说,用上这个东西没感觉方便,匿名函数主要是和其它函数搭配使用的呢,如下
1 res = map(lambda x:x**2,[1,5,7,4,8]) 2 for i in res: 3 print(i)
函数式编程介绍
函数是Python内建支持的一种封装,我们通过把大段代码拆成函数,通过一层一层的函数调用,就可以把复杂任务分解成简单的任务,这种分解可以称之为面向过程的程序设计。函数就是面向过程的程序设计的基本单元。
函数式编程中的函数这个术语不是指计算机中的函数(实际上是Subroutine),而是指数学中的函数,即自变量的映射。也就是说一个函数的值仅决定于函数参数的值,不依赖其他状态。比如sqrt(x)函数计算x的平方根,只要x不变,不论什么时候调用,调用几次,值都是不变的。
Python对函数式编程提供部分支持。由于Python允许使用变量,因此,Python不是纯函数式编程语言。
一、定义
简单说,"函数式编程"是一种"编程范式"(programming paradigm),也就是如何编写程序的方法论。
主要思想是把运算过程尽量写成一系列嵌套的函数调用。举例来说,现在有这样一个数学表达式:
(1 + 2) * 3 - 4
传统的过程式编程,可能这样写:
var a = 1 + 2;
var b = a * 3;
var c = b - 4;
函数式编程要求使用函数,我们可以把运算过程定义为不同的函数,然后写成下面这样:
var result = subtract(multiply(add(1,2), 3), 4);
这段代码再演进以下,可以变成这样
add(1,2).multiply(3).subtract(4)
这基本就是自然语言的表达了。再看下面的代码,大家应该一眼就能明白它的意思吧:
merge([1,2],[3,4]).sort().search("2")
因此,函数式编程的代码更容易理解。
高阶函数
变量可以指向函数,函数的参数能接收变量,那么一个函数就可以接收另一个函数作为参数,这种函数就称之为高阶函数。
1 def add(x,y,f): 2 return f(x) + f(y) 3 4 5 res = add(3,-6,abs) 6 print(res)
内置参数

内置参数详解 https://docs.python.org/3/library/functions.html?highlight=built#ascii
#compile f = open("函数递归.py") data =compile(f.read(),'','exec') exec(data) #print msg = "又回到最初的起点" f = open("tofile","w") print(msg,"记忆中你青涩的脸",sep="|",end="",file=f) # #slice # a = range(20) # pattern = slice(3,8,2) # for i in a[pattern]: #等于a[3:8:2] # print(i) # # #memoryview #usage: #>>> memoryview(b'abcd') #<memory at 0x104069648> #在进行切片并赋值数据时,不需要重新copy原列表数据,可以直接映射原数据内存, import time for n in (100000, 200000, 300000, 400000): data = b'x'*n start = time.time() b = data while b: b = b[1:] print('bytes', n, time.time()-start) for n in (100000, 200000, 300000, 400000): data = b'x'*n start = time.time() b = memoryview(data) while b: b = b[1:] print('memoryview', n, time.time()-start) 几个内置方法用法提醒



 浙公网安备 33010602011771号
浙公网安备 33010602011771号