闵可夫斯基距离(LP距离)、曼哈顿距离、欧式距离、切比雪夫距离、马哈拉诺比斯距离、相关系数、夹角余弦
标题闵可夫斯基距离(LP距离)、曼哈顿距离、欧式距离、切比雪夫距离、马哈拉诺比斯距离、相关系数、夹角余弦
在聚类中,可以将样本集合看作是向量空间中的点的集合,以该空间的距离表示样本之间相似度。常用的距离有闵可夫斯基距离,闵可夫斯基距离距离越大相似度越小,距离越小相似度越大。
定义:
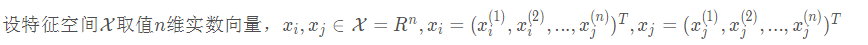
1.闵可夫斯基距离
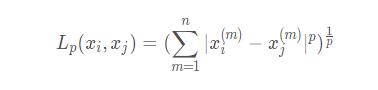
p>=1,p>=1,当p=1时是曼哈顿距离,p=2时是欧式距离,p=∞时是切比雪夫距离
2.曼哈顿距离
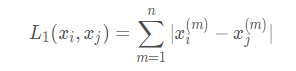
3.欧式距离
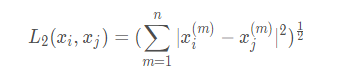
4.切比雪夫距离
切比雪夫距离是两个点之间距离最大的坐标系之间的距离。
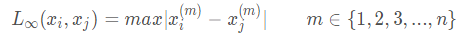
5.马哈拉诺比斯距离
马哈拉诺比斯距离,简称马氏距离,也是另一种常用距离,考虑各个分量之间的相关性与各个分量的尺度无关。马哈拉诺比斯距离越大相似度越小,距离越小相似度越大。

6. 相关系数
样本之间的相似度也可以用相关系数来表示。相关系数的绝对值接近于1样本岳相似;越接近于0,样本越不相似。
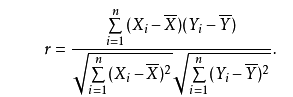
7. 夹角余弦
夹角余弦越接近于1样本越相似,越接近于0,样本越不相似。
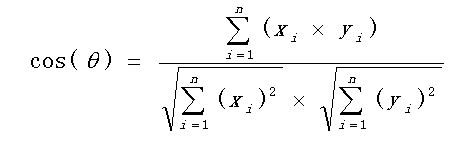




 浙公网安备 33010602011771号
浙公网安备 33010602011771号