L1&LL2正则化
L1与L2正则化的区别与联系
L1正则化和L2正则化的说明如下:
L1正则化:\(\min _{w} \frac{1}{2 n_{\text {samples}}}\|X w-y\|_{2}^{2}+\alpha\|w\|_{1}\) 绝对值之和
L2正则化:\(\min _{w}\|X w-y\|_{2}^{2}+\alpha\|w\|_{2}^{2}\) 平方和
L1正则化是指权值向量w中各个元素的绝对值之和,通常表示为||w||1
L2正则化是指权值向量w中各个元素的平方和然后再求平方根(可以看到Ridge回归的L2正则化项有平方符号),通常表示为||w||2
L1正则化可以产生稀疏权值矩阵,即产生一个稀疏模型,可以用于特征选择
L2正则化可以防止模型过拟合(overfitting);一定程度上,L1也可以防止过拟合
一般都会在正则化项之前添加一个系数,Python中用α表示,一些文章也用λ表示。这个系数需要用户指定。
L1 L2 区别:
相同点:都用于避免过拟合
不同点:L1可以让一部分特征的系数缩小到0,从而间接实现特征选择。所以L1适用于特征之间有关联的情况。
L2让所有特征的系数都缩小,但是不会减为0,它会使优化求解稳定快速。所以L2适用于特征之间没有关联的情况
- L2 regularizer :使得模型的解偏向于 norm 较小的 W,通过限制 W 的 norm 的大小实现了对模型空间的限制,从而在一定程度上避免了 overfitting 。不过 ridge regression 并不具有产生稀疏解的能力,得到的系数 仍然需要数据中的所有特征才能计算预测结果,从计算量上来说并没有得到改观。会选择更多的特征,这些特征都会接近于0。 最优的参数值很小概率出现在坐标轴上,因此每一维的参数都不会是0。当最小化||w||时,就会使每一项趋近于0
- L1 regularizer :** 它的优良性质是能产生稀疏性,因为最优的参数值很大概率出现在坐标轴上,这样就会导致某一维的权重为0 ,产生稀疏权重矩阵, 导致 W 中许多项变成零。** 稀疏的解除了计算量上的好处之外,更重要的是更具有“可解释性”csdn
L1稀疏性的原因
解空间形状直观理解
带正则项,相当于为目标函数的解空间进行了约束。当参数为2维时,为对于L2正则项,解空间为原型,L1正则项解空间为菱形。最优解必定是有且仅有一个交点。除非目标函数具有特殊的形状,否则和菱形的唯一交点大概率出现在截距处(即对应某一维度参数为0)。而对于圆形的解空间,总存在一个切点,且仅当某些特殊情况下,切点才会位于坐标轴上csdn

而正则化前面的系数α,可以控制L图形的大小。α越小,L的图形越大(上图中的黑色方框);α越大,L的图形就越小,可以小到黑色方框只超出原点范围一点点,这是最优点的值(w1,w2)=(0,w)中的w可以取到很小的值。
类似,假设有如下带L2正则化的损失函数:
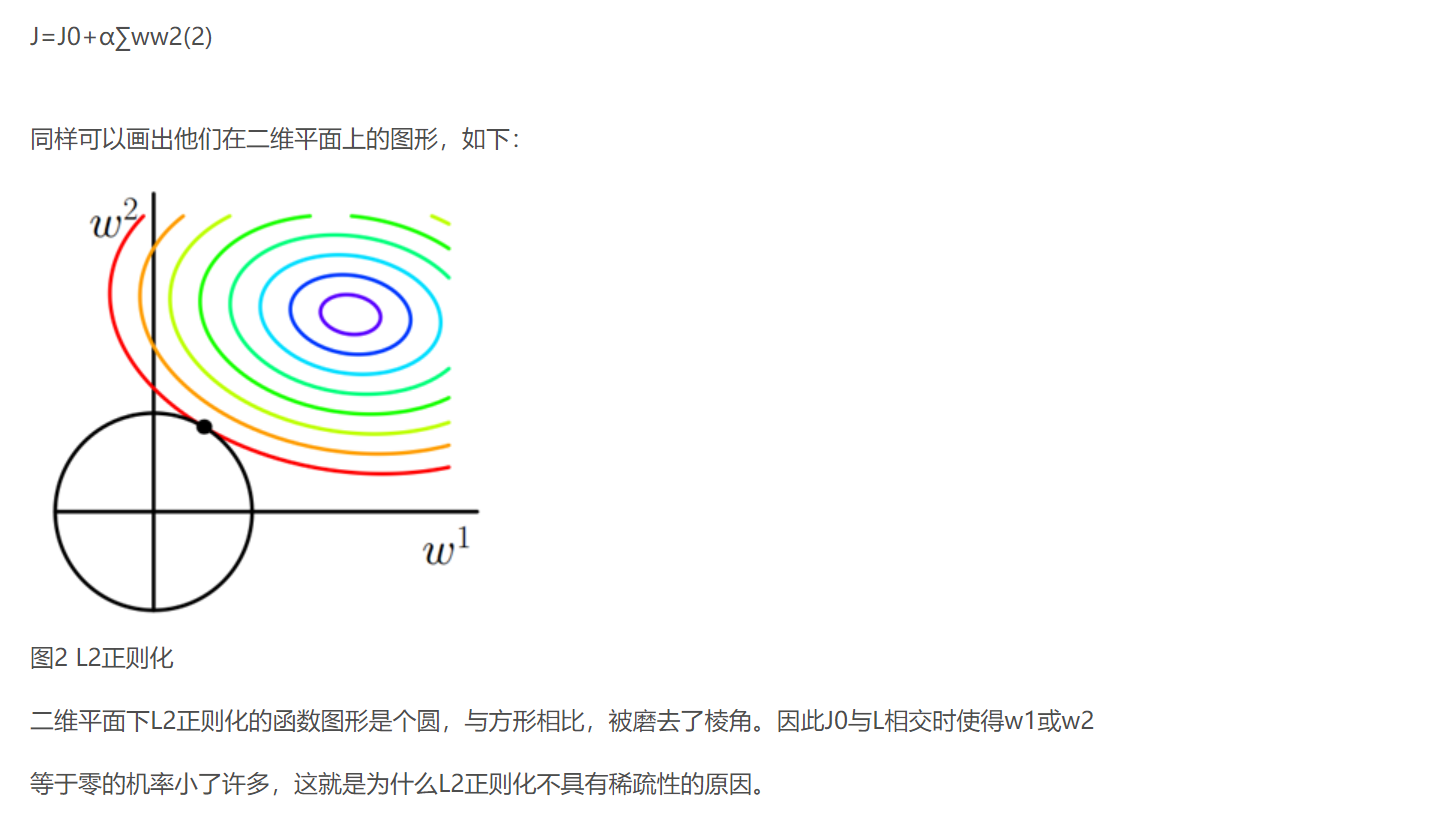

lasso 回归和岭回归(ridge regression)其实就是在标准线性回归的基础上分别加入 L1 和 L2 正则化(regularization)。
正则化
岭回归-Ridge
Loss function = OLS loss function +\(\alpha * \sum_{i=1}^{n} a_{i}^{2}\)
Lasso is great for feature selection, but when building regression models, Ridge regression should be your first choice.
datacamp
# Import necessary modules
from sklearn.linear_model import Ridge
from sklearn.model_selection import cross_val_score
# Setup the array of alphas and lists to store scores
alpha_space = np.logspace(-4, 0, 50)
ridge_scores = []
ridge_scores_std = []
# Create a ridge regressor: ridge
ridge = Ridge(normalize=True)
# Compute scores over range of alphas
# 给出很多a值,调参,就是超参数调参
for alpha in alpha_space:
# Specify the alpha value to use: ridge.alpha
ridge.alpha = alpha
# Perform 10-fold CV: ridge_cv_scores
# 用到了10折交叉验证进行的调参
ridge_cv_scores = cross_val_score(ridge, X, y, cv=10)
# Append the mean of ridge_cv_scores to ridge_scores
ridge_scores.append(np.mean(ridge_cv_scores))
# Append the std of ridge_cv_scores to ridge_scores_std
ridge_scores_std.append(np.std(ridge_cv_scores))
# Display the plot
display_plot(ridge_scores, ridge_scores_std)

Lasso_套索回归(最小绝对值收敛)
Loss function = OLS loss function +\(\alpha * \sum_{i=1}^{n}\left|a_{i}\right|\)
lasso一般用来进行特征选择
- hrinks the coefcients of less important features to exactly 0
# Import Lasso
from sklearn.linear_model import Lasso
# Instantiate a lasso regressor: lasso
lasso = Lasso(alpha=0.4, normalize=True)
# Fit the regressor to the data
lasso.fit(X, y)
# Compute and print the coefficients
lasso_coef = lasso.coef_
print(lasso_coef)
# Plot the coefficients
plt.plot(range(len(df_columns)), lasso_coef)
plt.xticks(range(len(df_columns)), df_columns.values, rotation=60)
plt.margins(0.02)
plt.show()



 浙公网安备 33010602011771号
浙公网安备 33010602011771号