1343：【例4-2】牛的旅行

【题目描述】

农民John的农场里有很多牧区。有的路径连接一些特定的牧区。一片所有连通的牧区称为一个牧场。但是就目前而言，你能看到至少有两个牧区不连通。现在，John想在农场里添加一条路径 ( 注意，恰好一条 )。对这条路径有这样的限制：一个牧场的直径就是牧场中最远的两个牧区的距离 ( 本题中所提到的所有距离指的都是最短的距离 )。考虑如下的两个牧场，图１是有5个牧区的牧场，牧区用“*”表示，路径用直线表示。每一个牧区都有自己的坐标：

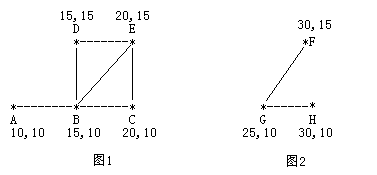
图１所示的牧场的直径大约是12.07106, 最远的两个牧区是A和E，它们之间的最短路径是A-B-E。

这两个牧场都在John的农场上。John将会在两个牧场中各选一个牧区，然后用一条路径连起来，使得连通后这个新的更大的牧场有最小的直径。注意，如果两条路径中途相交，我们不认为它们是连通的。只有两条路径在同一个牧区相交，我们才认为它们是连通的。

现在请你编程找出一条连接两个不同牧场的路径，使得连上这条路径后，这个更大的新牧场有最小的直径。

【输入】

第 1 行：一个整数N (1 <= N <= 150), 表示牧区数；

第 2 到 N+1 行：每行两个整数X，Y ( 0 <= X，Y<= 100000 )， 表示N个牧区的坐标。每个牧区的坐标都是不一样的。

第 N+2 行到第 2*N+1 行：每行包括N个数字 ( 0或1 ) 表示一个对称邻接矩阵。

例如，题目描述中的两个牧场的矩阵描述如下：

 A B C D E F G H 
A 0 1 0 0 0 0 0 0 
B 1 0 1 1 1 0 0 0 
C 0 1 0 0 1 0 0 0 
D 0 1 0 0 1 0 0 0 
E 0 1 1 1 0 0 0 0 
F 0 0 0 0 0 0 1 0 
G 0 0 0 0 0 1 0 1 
H 0 0 0 0 0 0 1 0

 

输入数据中至少包括两个不连通的牧区。

【输出】

只有一行，包括一个实数，表示所求答案。数字保留六位小数。

【输入样例】

8
10 10
15 10
20 10
15 15
20 15
30 15
25 10
30 10
01000000
10111000
01001000
01001000
01110000
00000010
00000101
00000010

【输出样例】

22.071068

#include <bits/stdc++.h>
using namespace std;

const int M = 100000 * 2; // 无穷大
struct Point {
    int x, y;
};

double dd(vector<Point> &a, int i, int j)
{
    double xx = a[i].x - a[j].x;
    double yy = a[i].y - a[j].y;
    return sqrt(xx * xx + yy * yy);
}

void floyd(vector<vector<double> > &d, vector<Point> &a)
{
    int n = a.size();
    for (int k = 1; k < n; k++) {
        for (int i = 1; i < n; i++) {
            for (int j = 1; j < n; j++) {
                if (i == j || k == i || k == j) {
                    continue;
                }
                double dd = d[i][k] + d[k][j];
                d[i][j] = min(d[i][j], dd);
            }
        }
    }
}

double f(vector<vector<double> > &d, vector<Point> &a)
{
    floyd(d, a);
    int n = a.size();
    vector<double> mx(n, 0);
    for (int i = 1; i < n; i++) {
        for (int j = 1; j < n; j++) {
            if (i == j || d[i][j] >= M) {
                continue;
            }
            mx[i] = max(mx[i], d[i][j]);
        }
    }
    double mn = INT_MAX;
    for (int i = 1; i < n; i++) {
        for (int j = 1; j < n; j++) {
            if (i == j || d[i][j] < M) {
                continue;
            }
            double d = dd(a, i, j);
            mn = min(mn, d + mx[i] + mx[j]);
        }
    }
    for (int i = 1; i < n; i++) {
        mn = max(mn, mx[i]);
    }
    return mn;
}

int main()
{
    // freopen("1.txt", "r", stdin);
    int n;
    cin >> n;
    vector<Point> a(n + 1); // 点
    for (int i = 1; i <= n; i++) {
        cin >> a[i].x >> a[i].y;
    }
    vector<vector<double> > d(n + 1, vector<double>(n + 1, M));
    for (int i = 1; i <= n; i++) {
        for (int j = 1; j <= n; j++) {
            char ch;
            cin >> ch;
            if (ch == '1') {
                d[i][j] = d[j][i] = dd(a, i, j);
            }
        }
        d[i][i] = 0;
    }
    cout << fixed << setprecision(6) << f(d, a);
    return 0;
}