结构和算法为程序的核心所在
先谈 数据和信息的关系 之前计基中背诵理解的
数据是信息的具体表现形式 数据是信息的载体
信息的符号化是数据 是数据加工后的结果
为了弄清五个XX概念 我最烦的就是xiajiba的概念
- 数据
- 数据元素
- 数据对象
- 数据类型
- 数据结构
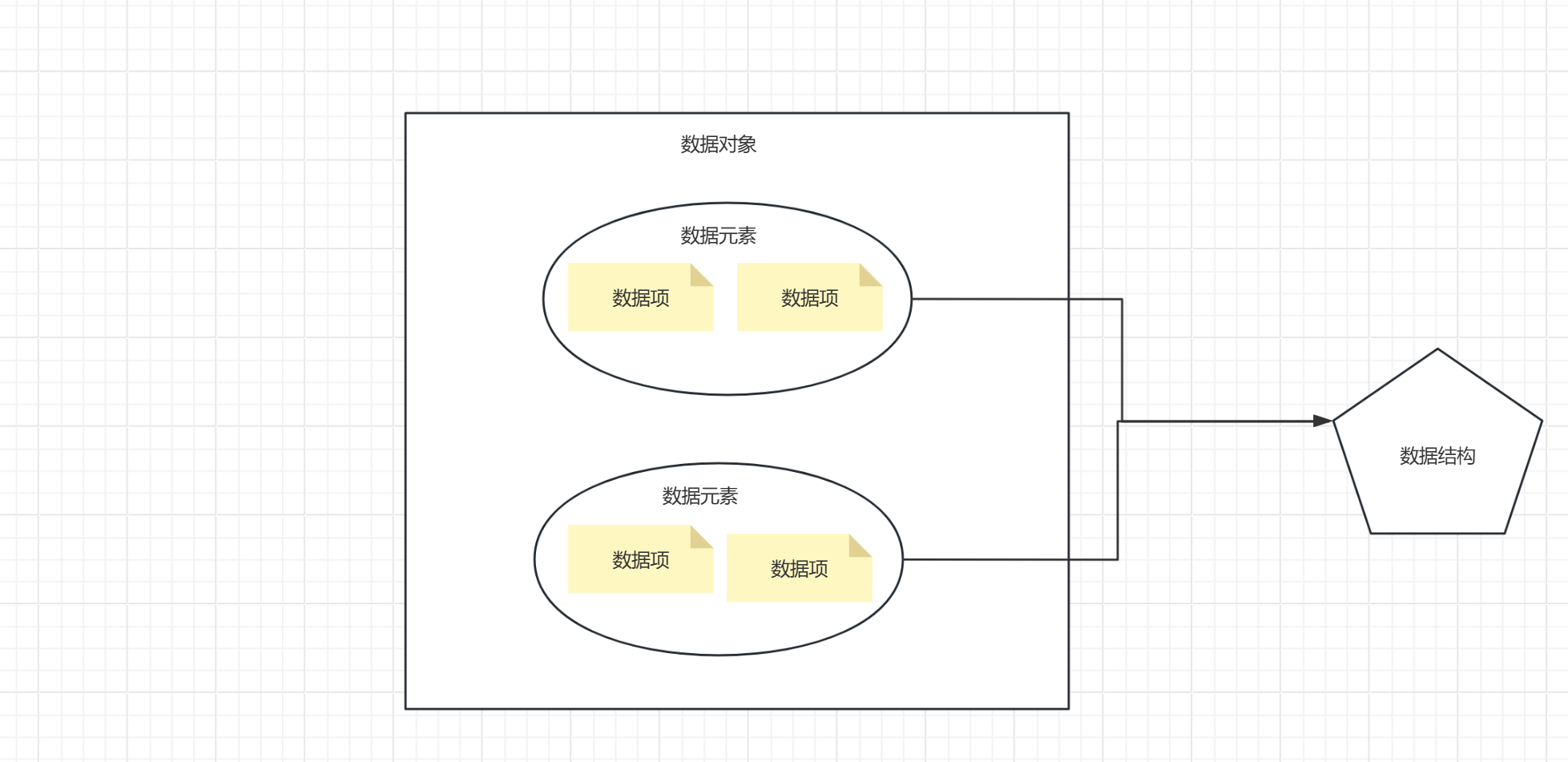
废话不多说上图
语言概述下: 数据元素是数据的基本单位 一个数据元素由若干个数据项组成
<数据项是构成数据元素的不可分割的最小单位>
数据对象是具有相同性质的数据元素的集合
数据结构相互之间存在一种或多种特定关系的数据元素的集合
至于数据类型 就是一个值的集合和定义(int float...)在此集合上的一组操作(加减乘除)的总称
我们重点研究的是数据结构
这里需要提到数据类型中"抽象数据类型":一个数学模型及定义在该数学模型上的一组操作
一个题
参考蚊香一眼的回答
看数据结构三要素
1.逻辑结构
顾名思义 逻辑 感觉是虚空的 是的 它与数据的存储无关 独立于计算机
其分为线性结构和非线性结构
!!!考点来了 :
线性结构:线性表 栈 队列
非线性结构:集合 数 图
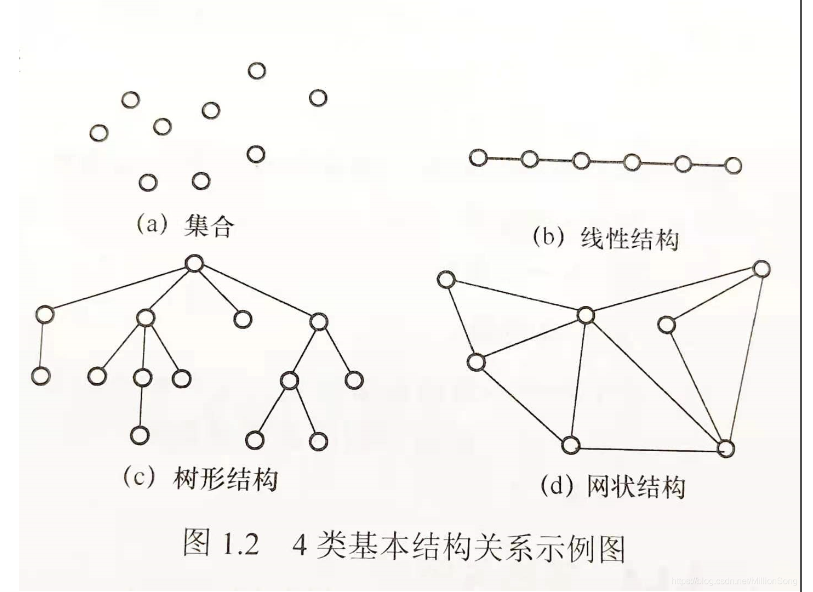
四种基本结构关系图:
对应的 无关系 一对一 一对多 多对多的关系
2.存储结构(物理结构)
用计算机语言实现的逻辑结构 依赖于计算机语言
然后我用大白话说一下存储结构有什么
1.顺序结构: 相邻元素 相邻的物理位置
2.链式存储:相邻元素 借助存储地址指针表示逻辑关系
3.索引存储:存储信息时 建立了索引表
4.散列存储: 哈希存储
看几个错题:
可以用()定义一个完整的数据结构
抽象数据类型
存储数据时 通常不仅要存储各数据元素的值 还要存储()
数据元素之间的关系
算法 效率的度量
算法对特定问题求解步骤的一种描述 它是指令的有限序列 五个特性 有穷性 确定性 可行性 有0个或多个输入 有1个或多个输出
考点 时间复杂度和空间复杂度
空间复杂度即算法所需的存储空间 就这
我们重点看时间复杂度
频度:算法中被重复执行的次数
频度之和T(n) 是问题规模n的函数
T(n)=O(f(n))
O是T(n)的数量级
三道例题解决:
1.
void fun(int n) {
int i = 1;
while (i < n)
i = i * 2;
}
两种方法
1.分析 t执行次数和i的变化情况:
时间复杂度为O(log2n)
2.分析 t执行次数和n的变化情况:
两种方法前面第一个需要带入条件中 个人认为第二种方法更实用全面性
2.
int Func(int n) {
if (n == 1)
return 1;
else return 2 * Func(n / 2) + n;
}
设计到了递归函数 只需关注递归函数的次数情况
这里时间复杂度为O(logn)可忽略对数函数的底数
3.
x = 0;
for (int i = 1; i < n; ++i) {
for (int j = i + 1; j < = n; ++j) {
x++;
}
}
分析这个的时候突然给我干死机了 主要是我在考虑内层循环的时候 又去想外层循环了
时间复杂度 即 外层循环X内存循环 O(n的平方)
over!!!






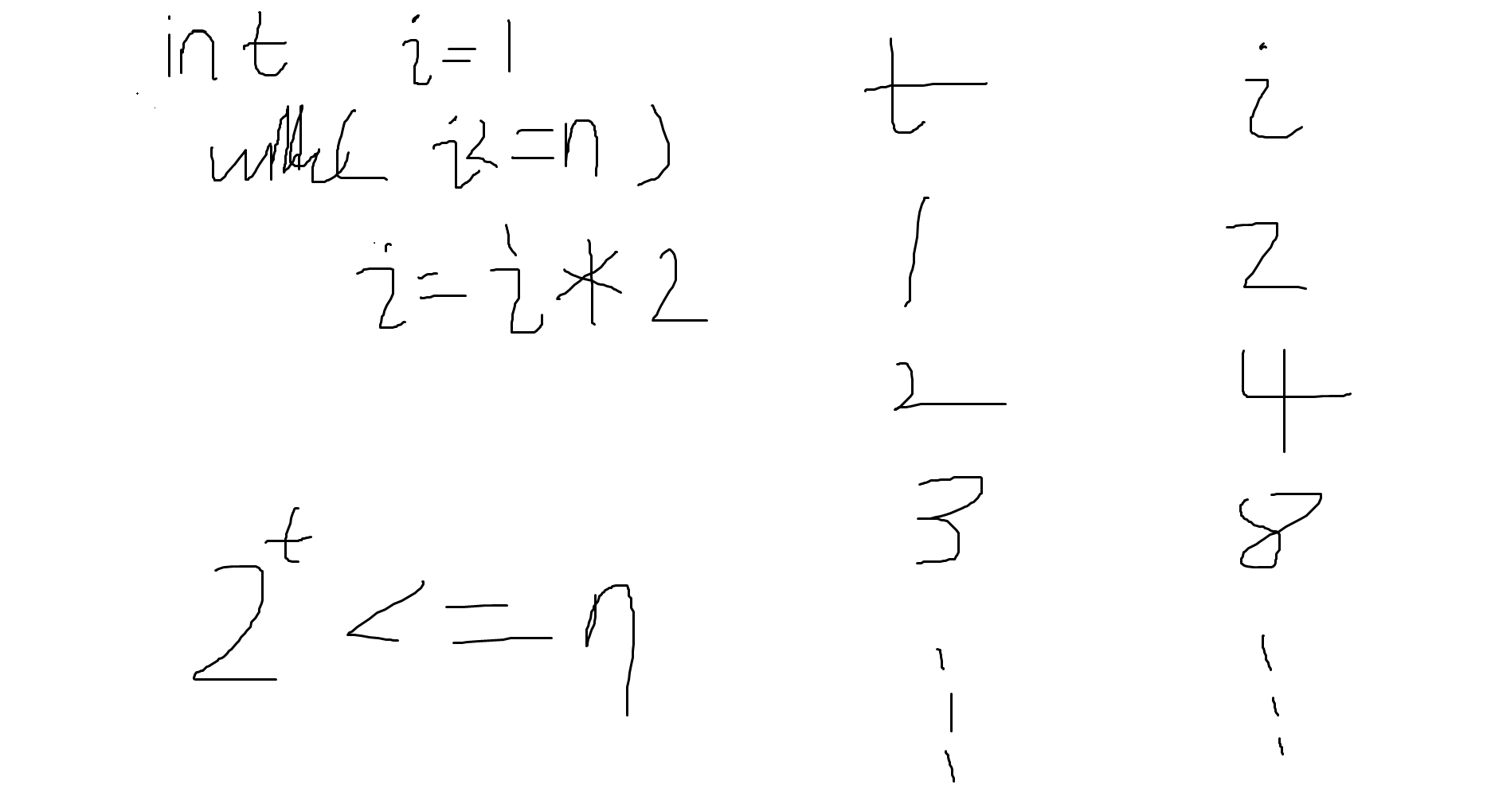
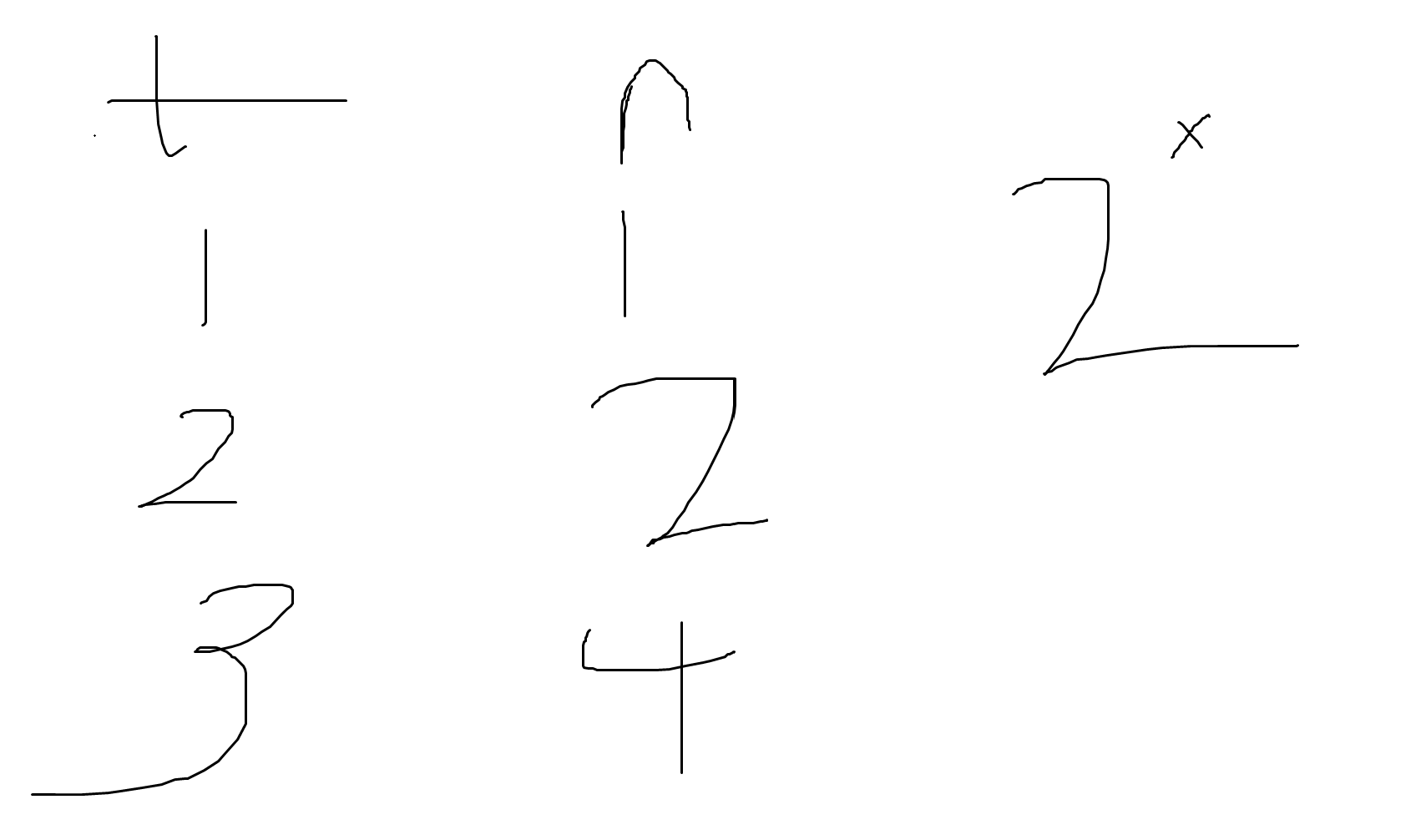
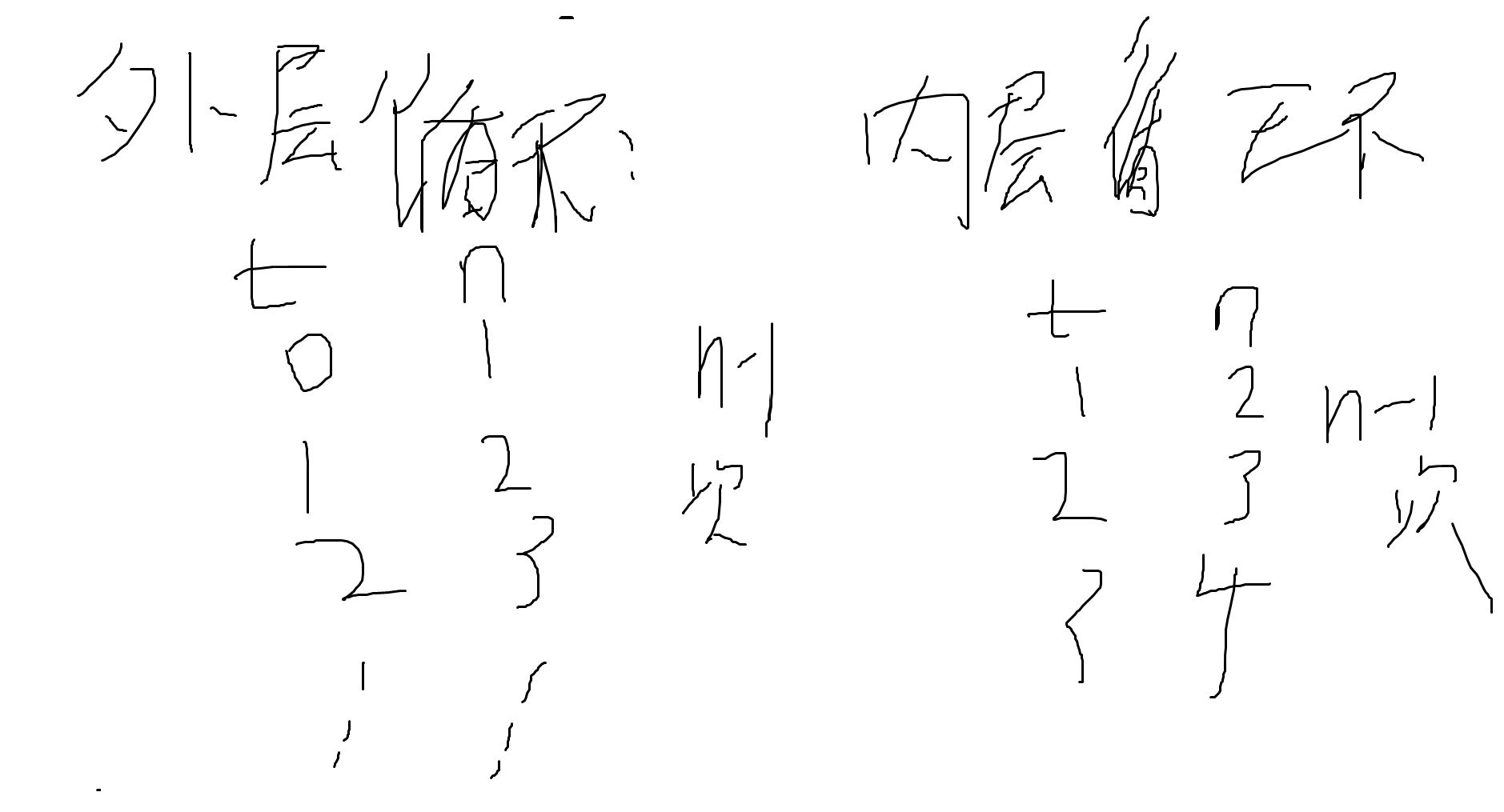

 浙公网安备 33010602011771号
浙公网安备 33010602011771号