斐波那契堆
斐波纳契堆(Fibonacci Heap)于 1984 年由 Michael L. Fredman 与 Robert E. Tarjan 提出,1987 年公开发表,名字来源于运行时分析所使用的斐波那契数。
斐波那契堆同二项堆(Binomial Heap)一样,也是一种可合并堆(Mergeable Heap)。与二项堆一样,斐波那契堆是由一组最小堆有序树构成,但堆中的树并不一定是二项树。与二项堆中树都是有序的不同,斐波那契堆中的树都是有根而无序的。
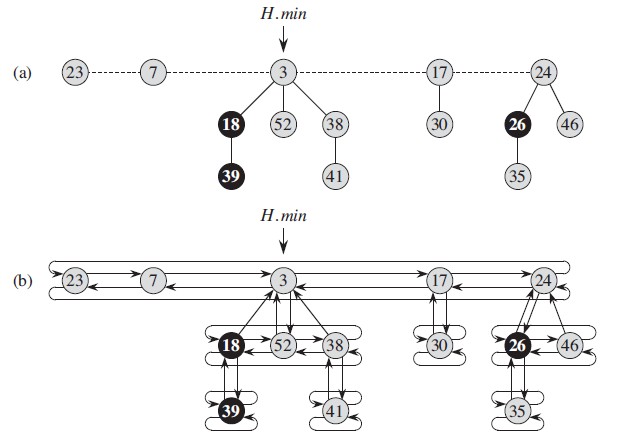
实际上,斐波那契堆松散地基于二项堆。如果不对斐波那契堆做任何 DECREASE-KEY 或 DELETE 操作,则堆中每棵树就和二项树一样。但是如果执行这两种操作,在一些状态下必须要破坏二项树的特征,比如DECREASE-KEY 或 DELETE 后,有的树高为 k,但是结点个数却少于 2k。这种情况下,堆中的树不是二项树。
斐波那契堆的优势是:不涉及删除元素的操作仅需要 O(1) 的平摊运行时间。
对于斐波那契堆上的各种可合并操作,关键思想是尽可能久地将工作推后。例如,当向斐波那契堆中插入新结点或合并两个斐波那契堆时,并不去合并树,而是将这个工作留给 EXTRACT-MIN 操作。
1 /*********************************************************************** 2 * File: FibonacciHeap.java 3 * Author: Keith Schwarz (htiek@cs.stanford.edu) 4 * 5 * An implementation of a priority queue backed by a Fibonacci heap, 6 * as described by Fredman and Tarjan. Fibonacci heaps are interesting 7 * theoretically because they have asymptotically good runtime guarantees 8 * for many operations. In particular, insert, peek, and decrease-key all 9 * run in amortized O(1) time. dequeueMin and delete each run in amortized 10 * O(lg n) time. This allows algorithms that rely heavily on decrease-key 11 * to gain significant performance boosts. For example, Dijkstra's algorithm 12 * for single-source shortest paths can be shown to run in O(m + n lg n) using 13 * a Fibonacci heap, compared to O(m lg n) using a standard binary or binomial 14 * heap. 15 * 16 * Internally, a Fibonacci heap is represented as a circular, doubly-linked 17 * list of trees obeying the min-heap property. Each node stores pointers 18 * to its parent (if any) and some arbitrary child. Additionally, every 19 * node stores its degree (the number of children it has) and whether it 20 * is a "marked" node. Finally, each Fibonacci heap stores a pointer to 21 * the tree with the minimum value. 22 * 23 * To insert a node into a Fibonacci heap, a singleton tree is created and 24 * merged into the rest of the trees. The merge operation works by simply 25 * splicing together the doubly-linked lists of the two trees, then updating 26 * the min pointer to be the smaller of the minima of the two heaps. Peeking 27 * at the smallest element can therefore be accomplished by just looking at 28 * the min element. All of these operations complete in O(1) time. 29 * 30 * The tricky operations are dequeueMin and decreaseKey. dequeueMin works 31 * by removing the root of the tree containing the smallest element, then 32 * merging its children with the topmost roots. Then, the roots are scanned 33 * and merged so that there is only one tree of each degree in the root list. 34 * This works by maintaining a dynamic array of trees, each initially null, 35 * pointing to the roots of trees of each dimension. The list is then scanned 36 * and this array is populated. Whenever a conflict is discovered, the 37 * appropriate trees are merged together until no more conflicts exist. The 38 * resulting trees are then put into the root list. A clever analysis using 39 * the potential method can be used to show that the amortized cost of this 40 * operation is O(lg n), see "Introduction to Algorithms, Second Edition" by 41 * Cormen, Rivest, Leiserson, and Stein for more details. 42 * 43 * The other hard operation is decreaseKey, which works as follows. First, we 44 * update the key of the node to be the new value. If this leaves the node 45 * smaller than its parent, we're done. Otherwise, we cut the node from its 46 * parent, add it as a root, and then mark its parent. If the parent was 47 * already marked, we cut that node as well, recursively mark its parent, 48 * and continue this process. This can be shown to run in O(1) amortized time 49 * using yet another clever potential function. Finally, given this function, 50 * we can implement delete by decreasing a key to -\infty, then calling 51 * dequeueMin to extract it. 52 */ 53 54 import java.util.*; // For ArrayList 55 56 /** 57 * A class representing a Fibonacci heap. 58 * 59 * @param T The type of elements to store in the heap. 60 * @author Keith Schwarz (htiek@cs.stanford.edu) 61 */ 62 public final class FibonacciHeap<T> { 63 /* In order for all of the Fibonacci heap operations to complete in O(1), 64 * clients need to have O(1) access to any element in the heap. We make 65 * this work by having each insertion operation produce a handle to the 66 * node in the tree. In actuality, this handle is the node itself, but 67 * we guard against external modification by marking the internal fields 68 * private. 69 */ 70 public static final class Entry<T> { 71 private int mDegree = 0; // Number of children 72 private boolean mIsMarked = false; // Whether this node is marked 73 74 private Entry<T> mNext; // Next and previous elements in the list 75 private Entry<T> mPrev; 76 77 private Entry<T> mParent; // Parent in the tree, if any. 78 79 private Entry<T> mChild; // Child node, if any. 80 81 private T mElem; // Element being stored here 82 private double mPriority; // Its priority 83 84 /** 85 * Returns the element represented by this heap entry. 86 * 87 * @return The element represented by this heap entry. 88 */ 89 public T getValue() { 90 return mElem; 91 } 92 /** 93 * Sets the element associated with this heap entry. 94 * 95 * @param value The element to associate with this heap entry. 96 */ 97 public void setValue(T value) { 98 mElem = value; 99 } 100 101 /** 102 * Returns the priority of this element. 103 * 104 * @return The priority of this element. 105 */ 106 public double getPriority() { 107 return mPriority; 108 } 109 110 /** 111 * Constructs a new Entry that holds the given element with the indicated 112 * priority. 113 * 114 * @param elem The element stored in this node. 115 * @param priority The priority of this element. 116 */ 117 private Entry(T elem, double priority) { 118 mNext = mPrev = this; 119 mElem = elem; 120 mPriority = priority; 121 } 122 } 123 124 /* Pointer to the minimum element in the heap. */ 125 private Entry<T> mMin = null; 126 127 /* Cached size of the heap, so we don't have to recompute this explicitly. */ 128 private int mSize = 0; 129 130 /** 131 * Inserts the specified element into the Fibonacci heap with the specified 132 * priority. Its priority must be a valid double, so you cannot set the 133 * priority to NaN. 134 * 135 * @param value The value to insert. 136 * @param priority Its priority, which must be valid. 137 * @return An Entry representing that element in the tree. 138 */ 139 public Entry<T> enqueue(T value, double priority) { 140 checkPriority(priority); 141 142 /* Create the entry object, which is a circularly-linked list of length 143 * one. 144 */ 145 Entry<T> result = new Entry<T>(value, priority); 146 147 /* Merge this singleton list with the tree list. */ 148 mMin = mergeLists(mMin, result); 149 150 /* Increase the size of the heap; we just added something. */ 151 ++mSize; 152 153 /* Return the reference to the new element. */ 154 return result; 155 } 156 157 /** 158 * Returns an Entry object corresponding to the minimum element of the 159 * Fibonacci heap, throwing a NoSuchElementException if the heap is 160 * empty. 161 * 162 * @return The smallest element of the heap. 163 * @throws NoSuchElementException If the heap is empty. 164 */ 165 public Entry<T> min() { 166 if (isEmpty()) 167 throw new NoSuchElementException("Heap is empty."); 168 return mMin; 169 } 170 171 /** 172 * Returns whether the heap is empty. 173 * 174 * @return Whether the heap is empty. 175 */ 176 public boolean isEmpty() { 177 return mMin == null; 178 } 179 180 /** 181 * Returns the number of elements in the heap. 182 * 183 * @return The number of elements in the heap. 184 */ 185 public int size() { 186 return mSize; 187 } 188 189 /** 190 * Given two Fibonacci heaps, returns a new Fibonacci heap that contains 191 * all of the elements of the two heaps. Each of the input heaps is 192 * destructively modified by having all its elements removed. You can 193 * continue to use those heaps, but be aware that they will be empty 194 * after this call completes. 195 * 196 * @param one The first Fibonacci heap to merge. 197 * @param two The second Fibonacci heap to merge. 198 * @return A new FibonacciHeap containing all of the elements of both 199 * heaps. 200 */ 201 public static <T> FibonacciHeap<T> merge(FibonacciHeap<T> one, FibonacciHeap<T> two) { 202 /* Create a new FibonacciHeap to hold the result. */ 203 FibonacciHeap<T> result = new FibonacciHeap<T>(); 204 205 /* Merge the two Fibonacci heap root lists together. This helper function 206 * also computes the min of the two lists, so we can store the result in 207 * the mMin field of the new heap. 208 */ 209 result.mMin = mergeLists(one.mMin, two.mMin); 210 211 /* The size of the new heap is the sum of the sizes of the input heaps. */ 212 result.mSize = one.mSize + two.mSize; 213 214 /* Clear the old heaps. */ 215 one.mSize = two.mSize = 0; 216 one.mMin = null; 217 two.mMin = null; 218 219 /* Return the newly-merged heap. */ 220 return result; 221 } 222 223 /** 224 * Dequeues and returns the minimum element of the Fibonacci heap. If the 225 * heap is empty, this throws a NoSuchElementException. 226 * 227 * @return The smallest element of the Fibonacci heap. 228 * @throws NoSuchElementException If the heap is empty. 229 */ 230 public Entry<T> dequeueMin() { 231 /* Check for whether we're empty. */ 232 if (isEmpty()) 233 throw new NoSuchElementException("Heap is empty."); 234 235 /* Otherwise, we're about to lose an element, so decrement the number of 236 * entries in this heap. 237 */ 238 --mSize; 239 240 /* Grab the minimum element so we know what to return. */ 241 Entry<T> minElem = mMin; 242 243 /* Now, we need to get rid of this element from the list of roots. There 244 * are two cases to consider. First, if this is the only element in the 245 * list of roots, we set the list of roots to be null by clearing mMin. 246 * Otherwise, if it's not null, then we write the elements next to the 247 * min element around the min element to remove it, then arbitrarily 248 * reassign the min. 249 */ 250 if (mMin.mNext == mMin) { // Case one 251 mMin = null; 252 } 253 else { // Case two 254 mMin.mPrev.mNext = mMin.mNext; 255 mMin.mNext.mPrev = mMin.mPrev; 256 mMin = mMin.mNext; // Arbitrary element of the root list. 257 } 258 259 /* Next, clear the parent fields of all of the min element's children, 260 * since they're about to become roots. Because the elements are 261 * stored in a circular list, the traversal is a bit complex. 262 */ 263 if (minElem.mChild != null) { 264 /* Keep track of the first visited node. */ 265 Entry<?> curr = minElem.mChild; 266 do { 267 curr.mParent = null; 268 269 /* Walk to the next node, then stop if this is the node we 270 * started at. 271 */ 272 curr = curr.mNext; 273 } while (curr != minElem.mChild); 274 } 275 276 /* Next, splice the children of the root node into the topmost list, 277 * then set mMin to point somewhere in that list. 278 */ 279 mMin = mergeLists(mMin, minElem.mChild); 280 281 /* If there are no entries left, we're done. */ 282 if (mMin == null) return minElem; 283 284 /* Next, we need to coalsce all of the roots so that there is only one 285 * tree of each degree. To track trees of each size, we allocate an 286 * ArrayList where the entry at position i is either null or the 287 * unique tree of degree i. 288 */ 289 List<Entry<T>> treeTable = new ArrayList<Entry<T>>(); 290 291 /* We need to traverse the entire list, but since we're going to be 292 * messing around with it we have to be careful not to break our 293 * traversal order mid-stream. One major challenge is how to detect 294 * whether we're visiting the same node twice. To do this, we'll 295 * spent a bit of overhead adding all of the nodes to a list, and 296 * then will visit each element of this list in order. 297 */ 298 List<Entry<T>> toVisit = new ArrayList<Entry<T>>(); 299 300 /* To add everything, we'll iterate across the elements until we 301 * find the first element twice. We check this by looping while the 302 * list is empty or while the current element isn't the first element 303 * of that list. 304 */ 305 for (Entry<T> curr = mMin; toVisit.isEmpty() || toVisit.get(0) != curr; curr = curr.mNext) 306 toVisit.add(curr); 307 308 /* Traverse this list and perform the appropriate unioning steps. */ 309 for (Entry<T> curr: toVisit) { 310 /* Keep merging until a match arises. */ 311 while (true) { 312 /* Ensure that the list is long enough to hold an element of this 313 * degree. 314 */ 315 while (curr.mDegree >= treeTable.size()) 316 treeTable.add(null); 317 318 /* If nothing's here, we're can record that this tree has this size 319 * and are done processing. 320 */ 321 if (treeTable.get(curr.mDegree) == null) { 322 treeTable.set(curr.mDegree, curr); 323 break; 324 } 325 326 /* Otherwise, merge with what's there. */ 327 Entry<T> other = treeTable.get(curr.mDegree); 328 treeTable.set(curr.mDegree, null); // Clear the slot 329 330 /* Determine which of the two trees has the smaller root, storing 331 * the two tree accordingly. 332 */ 333 Entry<T> min = (other.mPriority < curr.mPriority)? other : curr; 334 Entry<T> max = (other.mPriority < curr.mPriority)? curr : other; 335 336 /* Break max out of the root list, then merge it into min's child 337 * list. 338 */ 339 max.mNext.mPrev = max.mPrev; 340 max.mPrev.mNext = max.mNext; 341 342 /* Make it a singleton so that we can merge it. */ 343 max.mNext = max.mPrev = max; 344 min.mChild = mergeLists(min.mChild, max); 345 346 /* Reparent max appropriately. */ 347 max.mParent = min; 348 349 /* Clear max's mark, since it can now lose another child. */ 350 max.mIsMarked = false; 351 352 /* Increase min's degree; it now has another child. */ 353 ++min.mDegree; 354 355 /* Continue merging this tree. */ 356 curr = min; 357 } 358 359 /* Update the global min based on this node. Note that we compare 360 * for <= instead of < here. That's because if we just did a 361 * reparent operation that merged two different trees of equal 362 * priority, we need to make sure that the min pointer points to 363 * the root-level one. 364 */ 365 if (curr.mPriority <= mMin.mPriority) mMin = curr; 366 } 367 return minElem; 368 } 369 370 /** 371 * Decreases the key of the specified element to the new priority. If the 372 * new priority is greater than the old priority, this function throws an 373 * IllegalArgumentException. The new priority must be a finite double, 374 * so you cannot set the priority to be NaN, or +/- infinity. Doing 375 * so also throws an IllegalArgumentException. 376 * 377 * It is assumed that the entry belongs in this heap. For efficiency 378 * reasons, this is not checked at runtime. 379 * 380 * @param entry The element whose priority should be decreased. 381 * @param newPriority The new priority to associate with this entry. 382 * @throws IllegalArgumentException If the new priority exceeds the old 383 * priority, or if the argument is not a finite double. 384 */ 385 public void decreaseKey(Entry<T> entry, double newPriority) { 386 checkPriority(newPriority); 387 if (newPriority > entry.mPriority) 388 throw new IllegalArgumentException("New priority exceeds old."); 389 390 /* Forward this to a helper function. */ 391 decreaseKeyUnchecked(entry, newPriority); 392 } 393 394 /** 395 * Deletes this Entry from the Fibonacci heap that contains it. 396 * 397 * It is assumed that the entry belongs in this heap. For efficiency 398 * reasons, this is not checked at runtime. 399 * 400 * @param entry The entry to delete. 401 */ 402 public void delete(Entry<T> entry) { 403 /* Use decreaseKey to drop the entry's key to -infinity. This will 404 * guarantee that the node is cut and set to the global minimum. 405 */ 406 decreaseKeyUnchecked(entry, Double.NEGATIVE_INFINITY); 407 408 /* Call dequeueMin to remove it. */ 409 dequeueMin(); 410 } 411 412 /** 413 * Utility function which, given a user-specified priority, checks whether 414 * it's a valid double and throws an IllegalArgumentException otherwise. 415 * 416 * @param priority The user's specified priority. 417 * @throws IllegalArgumentException If it is not valid. 418 */ 419 private void checkPriority(double priority) { 420 if (Double.isNaN(priority)) 421 throw new IllegalArgumentException(priority + " is invalid."); 422 } 423 424 /** 425 * Utility function which, given two pointers into disjoint circularly- 426 * linked lists, merges the two lists together into one circularly-linked 427 * list in O(1) time. Because the lists may be empty, the return value 428 * is the only pointer that's guaranteed to be to an element of the 429 * resulting list. 430 * 431 * This function assumes that one and two are the minimum elements of the 432 * lists they are in, and returns a pointer to whichever is smaller. If 433 * this condition does not hold, the return value is some arbitrary pointer 434 * into the doubly-linked list. 435 * 436 * @param one A pointer into one of the two linked lists. 437 * @param two A pointer into the other of the two linked lists. 438 * @return A pointer to the smallest element of the resulting list. 439 */ 440 private static <T> Entry<T> mergeLists(Entry<T> one, Entry<T> two) { 441 /* There are four cases depending on whether the lists are null or not. 442 * We consider each separately. 443 */ 444 if (one == null && two == null) { // Both null, resulting list is null. 445 return null; 446 } 447 else if (one != null && two == null) { // Two is null, result is one. 448 return one; 449 } 450 else if (one == null && two != null) { // One is null, result is two. 451 return two; 452 } 453 else { // Both non-null; actually do the splice. 454 /* This is actually not as easy as it seems. The idea is that we'll 455 * have two lists that look like this: 456 * 457 * +----+ +----+ +----+ 458 * | |--N->|one |--N->| | 459 * | |<-P--| |<-P--| | 460 * +----+ +----+ +----+ 461 * 462 * 463 * +----+ +----+ +----+ 464 * | |--N->|two |--N->| | 465 * | |<-P--| |<-P--| | 466 * +----+ +----+ +----+ 467 * 468 * And we want to relink everything to get 469 * 470 * +----+ +----+ +----+---+ 471 * | |--N->|one | | | | 472 * | |<-P--| | | |<+ | 473 * +----+ +----+<-\ +----+ | | 474 * \ P | | 475 * N \ N | 476 * +----+ +----+ \->+----+ | | 477 * | |--N->|two | | | | | 478 * | |<-P--| | | | | P 479 * +----+ +----+ +----+ | | 480 * ^ | | | 481 * | +-------------+ | 482 * +-----------------+ 483 * 484 */ 485 Entry<T> oneNext = one.mNext; // Cache this since we're about to overwrite it. 486 one.mNext = two.mNext; 487 one.mNext.mPrev = one; 488 two.mNext = oneNext; 489 two.mNext.mPrev = two; 490 491 /* Return a pointer to whichever's smaller. */ 492 return one.mPriority < two.mPriority? one : two; 493 } 494 } 495 496 /** 497 * Decreases the key of a node in the tree without doing any checking to ensure 498 * that the new priority is valid. 499 * 500 * @param entry The node whose key should be decreased. 501 * @param priority The node's new priority. 502 */ 503 private void decreaseKeyUnchecked(Entry<T> entry, double priority) { 504 /* First, change the node's priority. */ 505 entry.mPriority = priority; 506 507 /* If the node no longer has a higher priority than its parent, cut it. 508 * Note that this also means that if we try to run a delete operation 509 * that decreases the key to -infinity, it's guaranteed to cut the node 510 * from its parent. 511 */ 512 if (entry.mParent != null && entry.mPriority <= entry.mParent.mPriority) 513 cutNode(entry); 514 515 /* If our new value is the new min, mark it as such. Note that if we 516 * ended up decreasing the key in a way that ties the current minimum 517 * priority, this will change the min accordingly. 518 */ 519 if (entry.mPriority <= mMin.mPriority) 520 mMin = entry; 521 } 522 523 /** 524 * Cuts a node from its parent. If the parent was already marked, recursively 525 * cuts that node from its parent as well. 526 * 527 * @param entry The node to cut from its parent. 528 */ 529 private void cutNode(Entry<T> entry) { 530 /* Begin by clearing the node's mark, since we just cut it. */ 531 entry.mIsMarked = false; 532 533 /* Base case: If the node has no parent, we're done. */ 534 if (entry.mParent == null) return; 535 536 /* Rewire the node's siblings around it, if it has any siblings. */ 537 if (entry.mNext != entry) { // Has siblings 538 entry.mNext.mPrev = entry.mPrev; 539 entry.mPrev.mNext = entry.mNext; 540 } 541 542 /* If the node is the one identified by its parent as its child, 543 * we need to rewrite that pointer to point to some arbitrary other 544 * child. 545 */ 546 if (entry.mParent.mChild == entry) { 547 /* If there are any other children, pick one of them arbitrarily. */ 548 if (entry.mNext != entry) { 549 entry.mParent.mChild = entry.mNext; 550 } 551 /* Otherwise, there aren't any children left and we should clear the 552 * pointer and drop the node's degree. 553 */ 554 else { 555 entry.mParent.mChild = null; 556 } 557 } 558 559 /* Decrease the degree of the parent, since it just lost a child. */ 560 --entry.mParent.mDegree; 561 562 /* Splice this tree into the root list by converting it to a singleton 563 * and invoking the merge subroutine. 564 */ 565 entry.mPrev = entry.mNext = entry; 566 mMin = mergeLists(mMin, entry); 567 568 /* Mark the parent and recursively cut it if it's already been 569 * marked. 570 */ 571 if (entry.mParent.mIsMarked) 572 cutNode(entry.mParent); 573 else 574 entry.mParent.mIsMarked = true; 575 576 /* Clear the relocated node's parent; it's now a root. */ 577 entry.mParent = null; 578 } 579 }


 浙公网安备 33010602011771号
浙公网安备 33010602011771号