LeetCode 15 三数之和

LeetCode 15 三数之和

1. 题目地址

    https://leetcode.cn/problems/3sum/submissions/

2. 题目解析

    这道题考察两个基本点：排序 + 双指针

3. 题解

    1.  要使用双指针算法的话，我们首先需要对数组进行排序（从小到大）。
    2.  排完序之后，我们先使用三个指针i,j,k。
    3.  首先，先让i从小到大遍历，从而确定nums[i]。确定完nums[i]之后，我们再对j和k采用双指针算法。(关于双指针算法可以参考之前的博客)
    4.  先让j指向数组的起始位置，k指向数组的最后一个位置。在指针移动的过程中：如果nums[j] + nums[k] + C(nums[i]) >= 0。那么，就需要让k--。因为，在nums[j]和C不变的情况下，只有让nums[k]变小，才可能为0。如果nums[j] + nums[k] + C == 0，代表找到了答案。如果nums[j] + nums[k] + C < 0的话，那么我们需要让j++,k不变。因为，如果nums[j] + nums[k] + C < 0的话，当j++之后，nums[j'] > nums[j]。此时，nums[j] + nums[k] + C 才可能 >= 0。如果在j++的同时，k重新开始遍历的话，那么nums[j'] + nums[k'] + C 一定 >= nums[j'] + nums[k] + C。此时是无用的遍历方式。因此，我们只需要让j++,k不变即可。这样的话：j只需要从头遍历到尾，k只需要从尾遍历到头。只需要O(2n)的时间复杂度。这样就达到了优化的效果。
    5.  由于外层循环需要遍历n次，内两层循环通过双指针算法进行了优化，也是O(n)的时间复杂度。这样的话，本题解的时间复杂度就由O(n^3)->O(n²)

    这道题还有一个难点就是：如何去重。
        1.  如果我们按照上述方式的话，我们是无法进行去重的。
        2.  因此，我们可以将i < j < k。这样的话，可以去掉一些重复的元组。为什么？
            2.1 
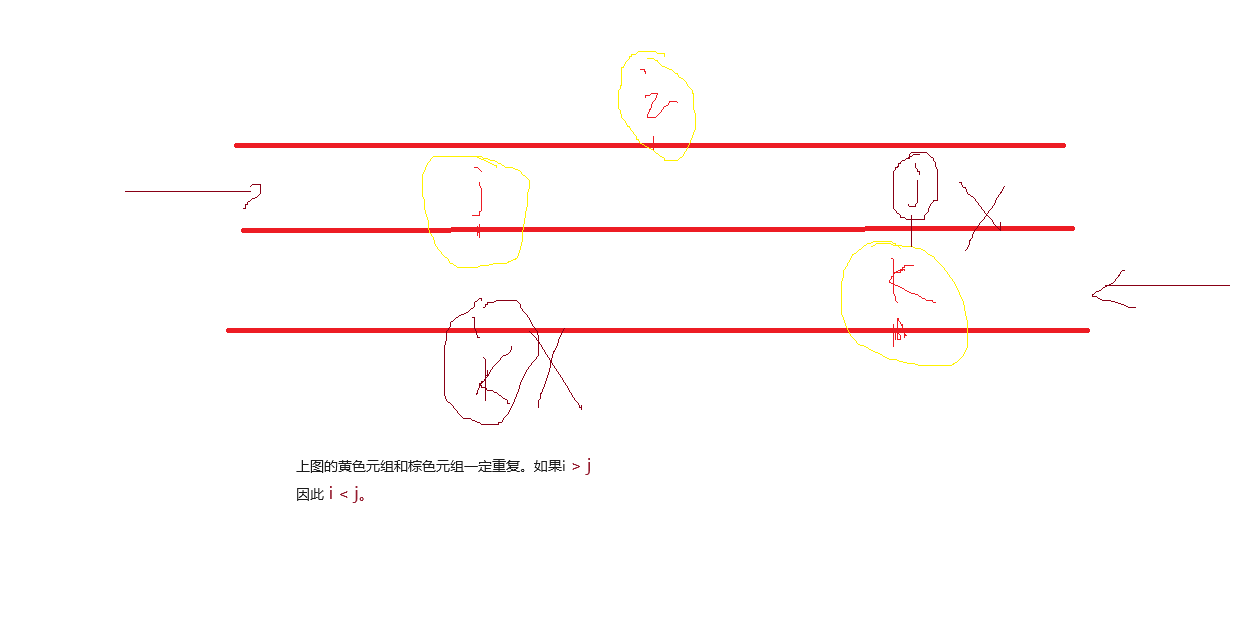
                根据上述第一个图，如果j < i的情况下，找到了一个数k。（上图黄色部分）
                那么，在j从左往右遍历的过程中，一定会遍历到跟黄色的k相同的位置。
                同理，在k从右往左遍历的过程中，一定会遍历到跟黄色的j相同的位置。
                此时，一定重复。
                因此：i 一定小于 j
            2.2 
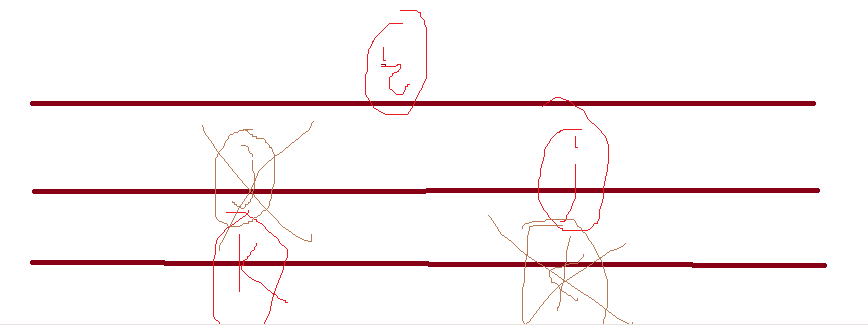
                现证明：j 一定小于 k。根据上述第二个图，如果j大于k（上图红色部分）时，找到了第一个无重复的元组。那么，由于j从左往右遍历，一定会遍历到跟红色的k相同的位置。（画叉处）
                同理，由于k从右往左遍历，一定会遍历到跟红色的j相同的位置。（画叉处）
                由于这两个画叉的位置一定在红色的位置之前，换句话说，如果红色的位置是答案，那么画叉的位置一定也是答案，且要更早输出。
                因此，矛盾。所以，j一定小于k。
            综上所述：i < j < k
        3.  如果i,j,k在遍历的过程中，当前的数和上一个数相等。那么此时不用再次遍历，得到的结果一定重复。因为：当i,j,k处于上一个数的时候，已经把所有的情况输出出来了。不用再次输出了。因此，如果当前数和上一个数相等，那么就跳过当前的数，直到跟上一个数不相等为止。

4. 代码

class Solution {
public:
    vector<vector<int>> threeSum(vector<int>& nums) {
        vector<vector<int>> res;
        //先排序
        sort(nums.begin(),nums.end());
        //遍历
        for(int i = 0; i < nums.size(); i ++){
            //去重
            if(i && nums[i] == nums[i-1]){
                continue;
            }
            for(int j = i + 1,k = nums.size() - 1; j < k; j ++){
                //去重
                if(j > i + 1 && nums[j] == nums[j-1]){
                    continue;
                }
                //试探法，总是找到满足条件的最小且最靠左的k
                /*原理：
                    1.  总是试探k前面的一个数，如果nums[i] + nums[j] + nums[k - 1] >= 0 。那么 nums[i] + nums[j] + nums[k] 一定大于0。此时，k一定--。
                    2.  如果nums[i] + nums[j] + nums[k-1] < 0,那么nums[i] + nums[j] + nums[k] 才有可能大于等于0。如果nums[i] + nums[j] + nums[k] == 0,此时需要将答案输出即可{nums[i],nums[j],nums[k]}。此时的k一定是满足条件的最小且最靠左的k。
                    3.  k - 1 一定大于j。因为，如果 k - 1 >= j ,那么当 k-1等于j且nums[i] + nums[j] + nums[k-1] >= 0时，k--。之后，k-1一定小于j，此时k跟j一定相等。这样的话，就跟题意矛盾了。因此k - 1一定大于j。
                */
                while(k - 1 > j && nums[i] + nums[j] + nums[k-1] >= 0){
                    k--;
                }
                if(nums[i] + nums[j] + nums[k] == 0){
                    
                    res.push_back({nums[i],nums[j],nums[k]});
                }
            }
        } 
        return res;
    }
};