高精度算法
1. 高精度算法类型
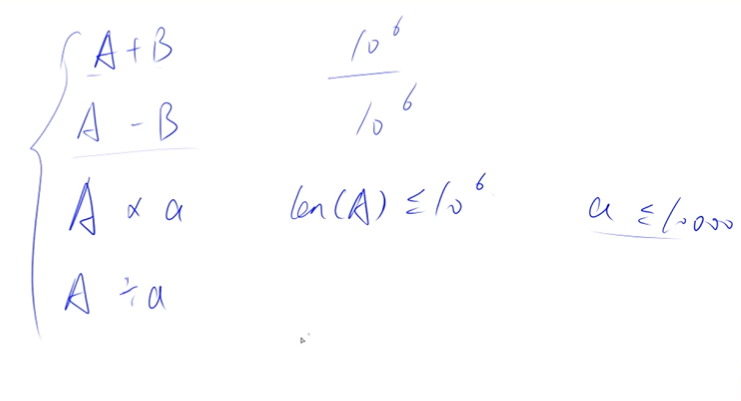
高精度算法主要分为四种:
1. 高精度加法
2. 高精度减法
3. 高精度乘法
4. 高精度除法
对于高精度加法和减法来看,相加的两个数的位数都<=10的6次方。
对于高精度乘法和除法,一般都是一个大的数乘或除一个小的数。大数的位数<=10的6次方,小数的数值一般<=10000。(注意这里位数和数值的区别)
具体的细节,可以查看上述的图例。
接下来,我们依次对这四种算法进行讲解。
值得注意的是:只有c/c++需要考虑高精度问题。对于java和python语言来讲不需要考虑高精度问题。因为java有专门的大整数/大浮点数类来完成高精度计算,并不需要自己实现。而python也内置了对应的算法,同样不需要自己动手实现。
2. 高精度加法思想

在进行大数相加之前,我们需要考虑一个核心问题:如何将大数存储下来?
方案一:如果我们采用int类型来存储的话,一定会爆掉。因为数的位数<=10的6次方,这是一个非常恐怖的大小。哪怕使用unsigned long long 都未必能存下。因此,我们不考虑用数值类型来存储。
方案二:我们使用数组来存储数的每一位。如果我们将数组的大小开到<=10的6次方的话,只需要声明数组number[1000000]即可。因此,使用数组存储是非常明智的选择。
当我们使用数组来存储大数时,还要注意一个问题:给定一个数字:123456789,我们应该要把这个数字的最高位放在数组下标为0的位置,还是要把这个数字的最低位放在数组下标为0的位置呢?
方案一:将数字的最高位放在数组下标为0的位置,这样的话:123456789分别对应数组下标012345678。若如此做,假设当两个数字相加的话,我们难免需要进位。如果产生了进位,我们需要将整个位数均往后挪动一位之后,再能存下进位的数字。这样是很麻烦的。
方案二:将数字的最低位放在数组下标为0的位置,这样的话:123456789分别对应数组下标876543210。若如此做,假设当两个数字相加的话,我们难免需要进位。如果产生了进位,我们只需要将进位的数字放在数组的最后面即可。并不需要挪动所有的位数,这样就非常简单了。
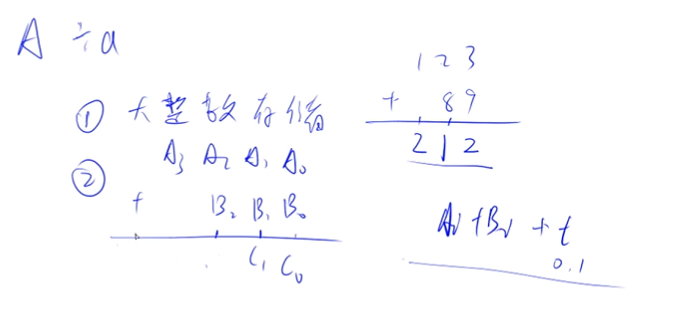
知道了上述的存储过程之后,我们接下来阐述一下高精度加法的思路:
1. 假设给定一个大数A和大数B。大数A的位数在数组中为:A3 A2 A1 A0(注意低位在前,高位在后),大数B的位数在数组中为:B2 B1 B0。
2. 遍历数组,从低位开始进行相加:如果Ai + Bi >= 10,那么就需要进位。此时我们应该要让进位设置为1。否则,进位=0。
3. 在相加的过程中,我们如何存储结果呢?很简单,如果存在来自上一位的进位,此时结果:(Ai + Bi + 1) % 10 即可。因为每一位都为0-9,不会超过10。如果不存在来自上一位的进位,此时结果:(Ai + Bi) % 10 即可。将结果放在新的数组中按照上述的存储顺序存储即可。
4. 在相加的过程中,如果两个大数位数不对等怎么办?很简单,对于不存在的位数,直接按照0处理即可。换句话来说:对于上述案例:A的位数:A3 A2 A1 A0 那么,B的位数:0 B2 B1 B0。按照这种形式相加即可。
3. 高精度加法模板
// C = A + B, A >= 0, B >= 0
vector<int> add(vector<int> &A, vector<int> &B)
{
if (A.size() < B.size()) return add(B, A);
vector<int> C;
int t = 0;
for (int i = 0; i < A.size(); i ++ )
{
t += A[i];
if (i < B.size()) t += B[i];
C.push_back(t % 10);
t /= 10;
}
if (t) C.push_back(t);
return C;
}
4. 高精度加法例题
https://www.acwing.com/problem/content/793/
//这里采用了vector容器
//也可以使用数组来进行替代,只需要额外记录长度即可
#include <iostream>
#include <cstdio>
#include <vector>
using namespace std;
vector<int> add(vector<int> &A,vector<int> &B){
vector<int> C;
//代表进位
int t = 0;
for(int i = 0;i < A.size() || i < B.size();i ++){
//计算A[i] + B[i] + t
if(i < A.size()){
t += A[i];
}
if(i < B.size()){
t += B[i];
}
//将结果放在大数C中
C.push_back(t % 10);
//查看是否进位
t /= 10;
}
//如果相加完之后,发现仍有进位,那么放在大数C的最高位即可
if(t == 1){
C.push_back(1);
}
return C;
}
int main(){
//由于数字很大,因此字符串接收
//通过遍历字符串,将每位数字放在数组里
string a,b;
cin >> a >> b; // a = "123456"
vector<int> A;
vector<int> B;
//按照规定次序放在数组里
for(int i = a.size() - 1; i >= 0;i --){ // A = [6,5,4,3,2,1]
A.push_back(a[i] - '0');
}
for(int i = b.size() - 1; i >= 0;i --){
B.push_back(b[i] - '0');
}
vector<int> C = add(A,B);
//将相加后的大数按照倒序输出
for(int i = C.size() - 1; i >= 0; i--){
printf("%d",C[i]);
}
return 0;
}
//c语言写法
#include <iostream>
#include <cstdio>
#include <cstring>
using namespace std;
char A_str[1000010];
int A[1000010];
char B_str[1000010];
int B[1000010];
int C[1000010];
int a_len,b_len,c_len;
void add(int A[],int B[]){
//代表进位
int t = 0;
for(int i = 0; i < a_len || i < b_len; i++){
if(i < a_len){
t += A[i];
}
if(i < b_len){
t += B[i];
}
C[c_len++] = t % 10;
t /= 10;
}
if(t == 1){
C[c_len++] = 1;
}
}
int main(){
scanf("%s%s",A_str,B_str);
//将字符串转换为数字
a_len = strlen(A_str);
b_len = strlen(B_str);
int cnt = 0;
for(int i = a_len - 1; i >= 0; i--){
A[cnt++] = A_str[i] - '0';
}
cnt = 0;
for(int i = b_len - 1; i >= 0; i--){
B[cnt++] = B_str[i] - '0';
}
add(A,B);
for(int i = c_len - 1; i >= 0;i --){
printf("%d",C[i]);
}
return 0;
}
作者:gao79138
链接:https://www.acwing.com/
来源:本博客中的截图、代码模板及题目地址均来自于Acwing。其余内容均为作者原创。
著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。
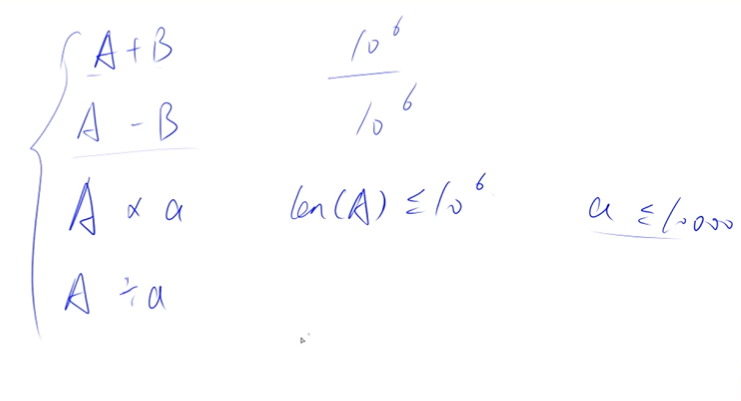

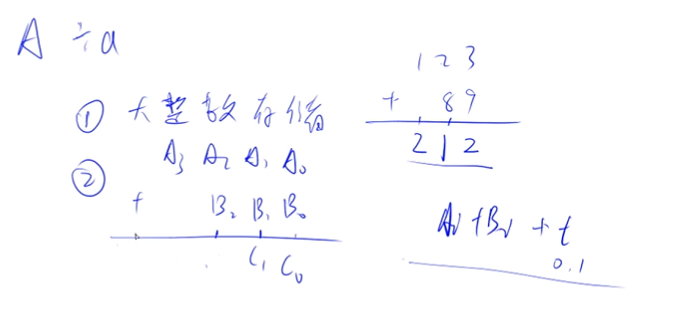



 浙公网安备 33010602011771号
浙公网安备 33010602011771号