KMP算法

KMP算法的用途

在一个串中查找是否出现过另一个串，这是KMP的看家本领

 

什么是前后缀？

前缀是指不包含最后一个字符的所有以第一个字符开头的连续子串；

后缀是指不包含第一个字符的所有以最后一个字符结尾的连续子串。

 

为什么要使用前缀表？

因为找到了最长相等的前缀和后缀，匹配失败的位置是后缀子串的后面，那么我们找到与其相同的前缀的后面重新匹配就可以了。

所以前缀表具有告诉我们当前位置匹配失败，跳到之前已经匹配过的地方的能力

 

如何求得前缀表？

计算最长相等前后缀的值

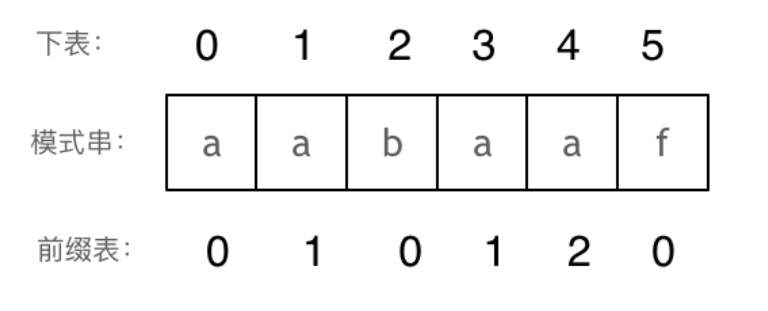
 前缀表的使用可以使指针免于回溯

 

什么是next数组？

next数组就是前缀表，但是很多实现都是把前缀表统一减一（右移一位，初始位置为-1）之后作为next数组

 

时间复杂度

KMP算法的时间复杂度是O(n+m)。

暴力的解法O(n × m)，KMP在字符串匹配中极大地提高了搜索的效率。

 

如何构造next数组？

1. 初始化
2. 处理前后缀不相同的情况
3. 处理前后缀相同的情况

 

构造next数组的函数代码

        void getnext(int *next,const string& s)//KMP算法
        {
            int j=-1;//j统一减1，s[j-1]就必须统一加1变成s[j]，保持位置不变
            next[0]=j;
            //i后缀末尾，j前缀末尾，j也等于最长相等前后缀长度
            for(int i=0;i<s.size();i++)
            {
                //前后缀不相等，回退，如果不相等一直退到最前端
                while(j>=0 && s[i]!=s[j+1])//j-1要保证不越界，故为j>=0
                {
                    j=next[j];
                }

                //前后缀相等
                if(s[i]==s[j+1])
                {
                    j++;
                }

                next[i]=j;
            }
        }

 

完整代码

class Solution {
public:

        void getnext(int *next,const string& s)
        {
            int j=0;
            next[0]=j;//最长相等前后缀值为0，j代表最长相等前后缀值，j也代表前缀末尾
            for(int i=1;i<s.size();i++)//i代表的是后缀末尾,所有从1开始
            {
                while(j>0 && s[i]!=s[j])
                {
                    j=next[j-1];//回退
                }

                if(s[i]==s[j])
                {
                    j++;
                }

                next[i]=j;
            }
        }

    int strStr(string haystack, string needle) {
            int next[needle.size()];
            int j=0;
            getnext(next,needle);
            if(needle.size()==0)
            {
                return 0;
            }

            for(int i=0;i<haystack.size();i++)
            {   
                while(j>0 && haystack[i]!=needle[j])//存疑，改成if程序也能跑通，且回退一次即可，有必要用while吗
                {
                    j=next[j-1];
                }

                if(haystack[i]==needle[j])
                {
                    j++;
                }

                if(j==needle.size())//当j指向空，即needle最后一位的下一位
                {
                    return (i-needle.size()+1);
                }
            }

            return -1;



    }


};