岛屿的周长

1.问题描述

给定一个包含 0 和 1 的二维网格地图，其中 1 表示陆地 0 表示水域。

网格中的格子水平和垂直方向相连（对角线方向不相连）。整个网格被水完全包围，但其中恰好有一个岛屿（或者说，一个或多个表示陆地的格子相连组成的岛屿）。

岛屿中没有“湖”（“湖” 指水域在岛屿内部且不和岛屿周围的水相连）。格子是边长为 1 的正方形。网格为长方形，且宽度和高度均不超过 100 。计算这个岛屿的周长。

示例 :

输入:

[[0,1,0,0],
 [1,1,1,0],
 [0,1,0,0],
 [1,1,0,0]]

输出: 16

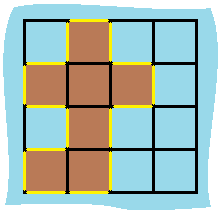
解释: 它的周长是下面图片中的 16 个黄色的边：

2.求解

迭代

• 遍历每个格子为1的陆地，查看其四条边是否为边界或是水域，若为将计数器加一。

代码如下

/*
 * 执行用时：7 ms, 在所有 Java 提交中击败了97.52% 的用户
 * 内存消耗：40 MB, 在所有 Java 提交中击败了24.93% 的用户
 * */
public int islandPerimeter(int[][] grid) {
    int ans = 0;
    int n = grid.length;
    int m = grid[0].length;
    for(int i = 0; i < n; i++){
        for(int j = 0; j < m; j++){
            if(grid[i][j] == 1){
                //判断上边
                if(i == 0 || grid[i-1][j] ==0){
                    ans++;
                }
                //判断右边
                if(j == m - 1 || grid[i][j + 1] == 0){
                    ans++;
                }
                //判断下边
                if(i == n - 1 || grid[i + 1][j] == 0){
                    ans++;
                }
                //判断右边
                if(j == 0 || grid[i][j - 1] == 0){
                    ans++;
                }
            }
        }
    }
    return ans;
}

• 时间复杂度：O(m * n)
• 空间复杂度：O(1)

递归

• 对于一块陆地，它分别查看它四条边的情况，结果只有两种
  • 毗邻水域或是边界，返回1，周长+1；
  • 毗邻陆地，对这块新的陆地继续发散，查看它四条边的情况
• 首先遍历数组拿到第一块陆地，然后从这块陆地发散出去，遇见边界水域就返回，遇见陆地就继续发散
• 为了防止重复遍历陆地死循环的情况出现，我们将已经遍历过的陆地值置为2，每次再判断下是否已经遍历过，若遍历过，就返回0（这块周长已经被计算过）

代码如下

/*
* 执行用时：10 ms, 在所有 Java 提交中击败了48.91% 的用户
* 内存消耗：40.3 MB, 在所有 Java 提交中击败了7.12% 的用户*/
public int islandPerimeter(int[][] grid) {
    //遍历格子拿到第一个陆地，执行递归函数
    for(int i = 0;i < grid.length;i++){
        for(int j = 0; j < grid[0].length;j++){
            if(grid[i][j] == 1) {
                return dfs(grid, i, j);
            }
        }
    }
    return 0;
}

int dfs(int[][] grid, int r, int c) {
    //到达边界，周长加1
    if (!(0 <= r && r < grid.length && 0 <= c && c < grid[0].length)) {
        return 1;
    }
    //到达水域，周长加1
    if (grid[r][c] == 0) {
        return 1;
    }
    //已经遍历过，返回0
    if (grid[r][c] == 2) {
        return 0;
    }
    grid[r][c] = 2;
    //三种情况都排出后，说明毗邻陆地，继续执行递归
    return dfs(grid, r - 1, c) + dfs(grid, r + 1, c) + dfs(grid, r, c - 1) + dfs(grid, r, c + 1);
}

• 时间、空间复杂度均为：O(m * n)