[DS 小计] 虚树
概念
什么是虚树？
通俗的来说，虚树是原树的一些点集组成的树，这些点是一些关键点。
在树形 dp 遍历中，如果每次都遍历整棵树会很浪费时间，这时候虚树就派上用场了。
简介
虚树的节点有哪些？
在 dp 中，我们建立虚树包含着关键节点和关键节点的任意二者的 \(\text{lca}\) 。
到这里，你已经会 \(O(k^2)\) 枚举 lca 的方法构建虚树了。
构造
我们来证明几个性质。
结论 \(1\)
根据 dfn 排序后的序列，对于任意 \(x_1,x_2,x_3,x_4,...x_n\)，其中 \(dfn_{x_1}<dfn_{x_2}..<dfn_{x_n} ，\)有 \(\text{lca}(x_1,x_n)=\text{lca}(\text{lca}(x_1,x_2),\text{lca}(x_2,x_3),...\text{lca}(x_{n-1},x_n),)\) 。
证明很简单，因为是按照 dfn 序列排序的，所以可以看成从左往右的点，对于 \(\text{lca}(1\to x-1)\)，新的点 \(x\) 肯定是会要么在前 \(x-1\) 个点的子树内，这时候就是原 \(lca\) ，否则子树外的话，就是和字数内任取一个点的 lca 即可。
结论 \(2\)
\(\text{lca}(x_1,x_n)\in \{\text{lca}(\text{lca}(x_1,x_2),\text{lca}(x_2,x_3),...\text{lca}(x_{n-1},x_n))\}\) 。
这个结论显然，这一定是这些 \(lca\) 中深度最小的那个点。深度最小的那个 \(lca\) 肯定是所有点的 \(lca\) .
也可以这样理解。
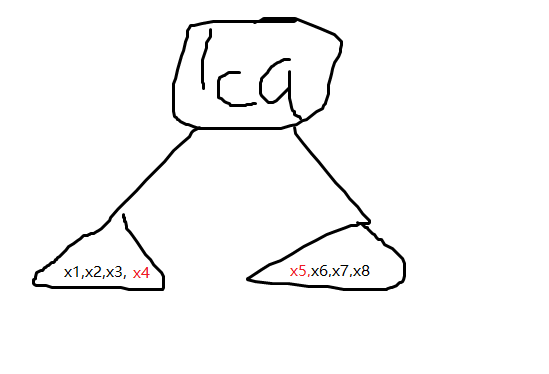
看图，明显，是有一对跨过 \(lca\) 的点对的。所以，结论正确。
所以，我们证明了一个很重要的性质：对于一个点集 \(U\) ，若将 \(U\) 中任意两两 \(\text{lca}\) 加入点集 \(V\) ，\(|V|\) \(\le\) \(|U|-1\)
也就是说，我们能证明，虚树中的点都是经过 dfn 排序后任意两个节点的 \(\text{lca}\) 。
构造方法
- 第一步，将所有点按照 dfn 排序
- 第二步，将相邻点的 \(\text{lca}\) 加入点集。
- 第三步，将所有点集内的点按 dfn 排序。
- 第四步，连接相邻点对即可。
这里详细讲讲怎么连接相邻点对。
对于相邻的 \(x,y\) ，我们连接 \(y\leftrightarrow\text{lca}(x,y)\)。
这样为什么是对的呢？
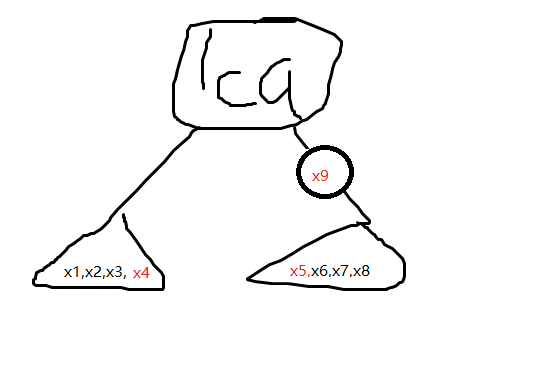
我们再看这个图。
如果遍历到 \(x_4\) ，很明显，它会找到另一棵子树 dfn 最小，最上面的节点， \(x_9\) ，让 \(x_9\) 和 \(lca\) 连边。
通俗的来说，这个过程是 \(x_2\to x_n\) 找父亲的过程。
那么谁是 \(x_9\) 的父亲呢？上一个节点不在 \(x_9\) 子树内，那上一个 \(y\) 有两种可能。
- 如果 \(y\) 是 \(x\) 的父亲，那么它们两个之间连边没问题。
- 如果 \(y\) 和 \(x\) 是兄弟节点，那么它们是祖先间最近的兄弟，它们的祖先就是 \(x\) 的父亲。
是不是很简单？时间复杂度因为排序很明显是 \(O(k\log k)\) 。
这样就做完了。
