队列详解及java实现
导读
栈和队列是有操作限制的线性表。
目录
1、队列的概念、特点、存储结构。
2、栈队列的java实现。
概念
队列是一种在一端进行插入,而在另一端进行删除的线性表。
1、队列的插入端称为队尾;队列的删除端称为队头。(好比火车进隧道)
2、队列的插入操作称为入队(push),删除操作称为出队(pop)。
特点
队列就像一列进入隧道的火车,隧道就是队列,火车车厢就是元素,进入隧道就是从隧道的这头(队尾)插入元素,出隧道就是从隧道的另一头(队头)删除元素。所以是“先进先出”的特点。
存储结构
类似栈有顺序队和链式队两种。
java实现
我们可以围绕栈的4个元素来实现队列:
2状态:是否队空;是否队满。
2操作:进队push;出队pop。
顺序队的实现
顺序队列的实现也可以使用数组来完成,同栈的实现一样,只是栈是在同一端进行压栈和进栈操作,而队列是在一端做push,另一端做pop操作。
可以看一下下面的队列操作示意图:
我们在实现顺序栈时使用头指针“front”和尾指针“rear”分别进行出队和入队操作,但普通的队列如上图所示,会发生“假溢出”现象,所以我们通常将数组弄成一个环状,即队头和队尾相连,这样就形成了“循环队列”,同时也解决了“假溢出”现象。循环队列是改进版的顺序队列。
如图:
对于普通队列的push或pop我们只需要对尾指针或头指针进行自增操作即可,但是循环队列我们就不能单纯的进行自增,当front或rear=maxSize-1时我们就不能进行自增操作了,比如一个队列尾长度为4的数组datas[4],那么当front或rear需要在0,1,2,3之间进行循环“推进”,以此达到循环队列的效果。所以我们可以使用rear = (rear+1)%maxSize ;front = (front+1)%maxSize ;公式进行指针计算。
需要注意的是:队空状态的条件为:front = rear。而如果整个队列全部存满数据那么,队满的条件也是front = rear;所以循环队列需要损失一个存储空间,如下图:
解决了这些问题我们就可以很轻松地实现循环队列了:
1 package test; 2 3 public class SqQueue<T>{ 4 private T[] datas;//使用数组作为队列的容器 5 private int maxSize;//队列的容量 6 private int front;//头指针 7 private int rear;//尾指针 8 9 //初始化队列 10 public SqQueue(int maxSize){ 11 if(maxSize<1){ 12 maxSize = 1; 13 } 14 this.maxSize = maxSize; 15 this.front = 0; 16 this.rear = 0; 17 this.datas = (T[])new Object[this.maxSize]; 18 } 19 20 //两个状态:队空&队满 21 public boolean isNull(){ 22 if(this.front == this.rear) 23 return true; 24 else 25 return false; 26 } 27 28 public boolean isFull(){ 29 if((rear+1)%this.maxSize==front) 30 return true; 31 else 32 return false; 33 } 34 35 //初始化队列 36 public void initQueue(){ 37 this.front = 0; 38 this.front = 0; 39 } 40 41 //两个操作:进队&出队 42 public boolean push(T data){ 43 if(isFull()) 44 return false;//队满则无法进队 45 else{ 46 datas[rear] = data;//进队 47 rear = (rear+1) % maxSize;//队尾指针+1. 48 return true; 49 } 50 } 51 public T pop(){ 52 if(isNull()) 53 return null;//对空无法出队 54 else{ 55 T popData = datas[front++];//出队 56 front = (front+1) % maxSize;//队头指针+1 57 return popData; 58 } 59 } 60 61 //get() 62 public T[] getDatas() { 63 return datas; 64 } 65 66 public int getMaxSize() { 67 return maxSize; 68 } 69 70 public int getFront() { 71 return front; 72 } 73 74 public int getRear() { 75 return rear; 76 } 77 }
测试:
1 package test; 2 3 import org.junit.Test; 4 5 public class testQueue { 6 7 @Test 8 public void fun(){ 9 SqQueue<Character> queue = new SqQueue<Character>(4); 10 11 //判断 12 System.out.println("队列是否为空:"+queue.isNull()); 13 14 //入队A,B,C 15 queue.push('A'); 16 queue.push('B'); 17 queue.push('C'); 18 19 System.out.println("队列是否为满:"+queue.isFull()); 20 21 //出队 22 Character data = queue.pop(); 23 System.out.println("出队:"+data); 24 } 25 }
链队的实现
如图所示:
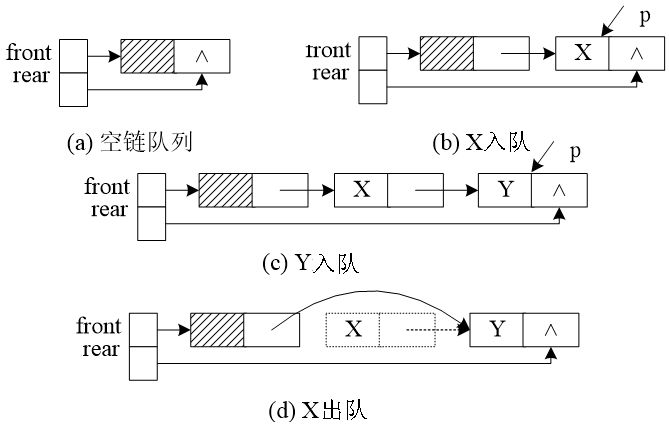
链队的实现很简单,只要理解了链表的操作和队列的特点即可。
1 package test; 2 3 public class LinkQueue<T>{ 4 private QNode<T> front;//队头指针 5 private QNode<T> rear;//队尾指针 6 private int maxSize;//为了便于操作,使用这个变量表示链队的数据容量 7 8 //初始化 9 public LinkQueue(){ 10 this.front = new QNode<T>(); 11 this.rear = new QNode<T>(); 12 this.maxSize = 0; 13 } 14 15 //初始化队列 16 public void initQueue(){ 17 front.next = null; 18 rear.next = null; 19 maxSize = 0; 20 } 21 22 //队空判断 23 public boolean isNull(){ 24 if(front.next==null || rear.next==null) 25 return true; 26 else 27 return false; 28 } 29 30 //进队 31 public void push(QNode<T> node){ 32 if(isNull()){ 33 //第一次 34 front.next = node; 35 rear.next = node; 36 maxSize++; 37 } 38 else{ 39 node.next = front.next; 40 front.next = node; 41 maxSize++; 42 } 43 } 44 //出队 45 public QNode<T> pop(){ 46 if(isNull()) 47 return null;//队为空时,无法出队 48 else if(maxSize==1){ 49 //队只有一个元素时直接初始化即可 50 QNode<T> node = front.next; 51 initQueue(); 52 return node; 53 } 54 else{ 55 //准备工作 56 QNode<T> p = front;//使用p指针来遍历队列 57 for(int i=1;i<maxSize-1;i++) 58 p = p.next; 59 //pop 60 QNode<T> node = rear.next; 61 rear.next = p.next; 62 maxSize--; 63 return node; 64 } 65 } 66 67 } 68 69 //链队结点 70 class QNode<T>{ 71 private T data;//数据域 72 public QNode<T> next;//指针域 73 74 //初始化1 75 public QNode(){ 76 this.data = null; 77 this.next = null; 78 } 79 //初始化2 80 public QNode(T data){ 81 this.data = data; 82 this.next = null; 83 } 84 85 public T getData() { 86 return data; 87 } 88 public void setData(T data) { 89 this.data = data; 90 } 91 92 }
测试:
1 package test; 2 3 import org.junit.Test; 4 5 public class testQueue { 6 7 @Test 8 public void fun(){ 9 LinkQueue<Integer> lq = new LinkQueue<Integer>(); 10 11 System.out.println("队列是否为空:"+lq.isNull()); 12 13 //依次插入1、2、3、4 14 lq.push(new QNode<Integer>(1)); 15 lq.push(new QNode<Integer>(2)); 16 lq.push(new QNode<Integer>(3)); 17 lq.push(new QNode<Integer>(4)); 18 19 //依次出队 20 System.out.println("依次出队:"); 21 while(!lq.isNull()){ 22 System.out.println(lq.pop().getData()); 23 } 24 25 } 26 }

 浙公网安备 33010602011771号
浙公网安备 33010602011771号