省选复习
复习大纲
杂项/技巧
差分和前缀和,树上差分。二分,整体二分,二分斜率。分治。
P4173 残缺的字符串:用 FFT 做带通配符的匹配,将通配符的值设为 0,然后平方去掉绝对值即可,复杂度 \(O(n\log n)\)。
P4563 [JXOI2018] 守卫,有时直觉不一定准确,甚至和正解完全相反。
有时我们可以先暴力 \(O(n)\) 枚举,然后快速计算贡献。P1117 [NOI2016] 优秀的拆分。
一些点之间的最短路:P5304 [GXOI/GZOI2019] 旅行者,按照点在 \(2^i\) 处的值分类进行 \(\log n\) 次最短路,复杂度 \(O(n\log^2n)\)。
可以换一种方式来表达,比如将序列放在值域上考虑。
P6653 [YsOI2020] 造林:无根树树哈希。
P5305 [GXOI/GZOI2019] 旧词,考虑差分,\(val_x=dep_x^k-(dep_x-1)^k\),所以 \(dep_{\operatorname{lca}(x,y)}^k\) 就是从 \(\operatorname{lca}(x,y)\) 到根的所有节点的权值和,这样做就很方便了。
可以研究一下区间和区间之间的关系对答案的影响。
P3785 [SDOI2017] 文本校正:大力分类讨论。
将修改和询问放在一起做整体二分:P2617 Dynamic Rankings
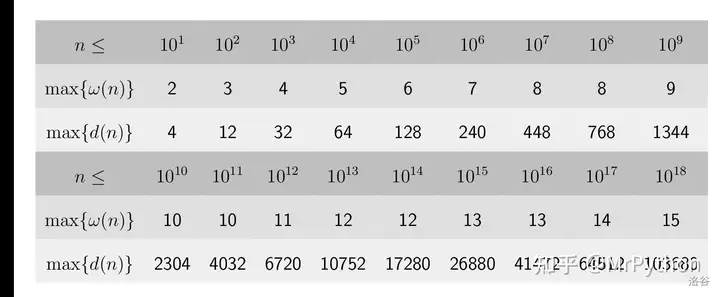
一个数的因子数很小:
对操作/形态进行差分:P3348 [ZJOI2016] 大森林。
分治:P3350 [ZJOI2016] 旅行者,可以按行分治也可以按列分治,具体按照哪行哪列的长度来决定对哪个维度分治。
P4064 [JXOI2017] 加法:二分后贪心统计即可。
随机数据下最坏情况出现的概率很小,所以我们可以只维护一部分信息就能保证正确性。P3732 [HAOI2017] 供给侧改革。
\(\gcd\) 是可以差分的,因此可以将区间内的数和 \(x\) 进行 \(\gcd\) 变为单点修改,辗转相除法:\(\gcd(a,b)=\gcd(a,b-a)\) 。
总之大胆推式子就完事了,然后对 \(P=2,P=5\) 特判一下即可:P3245 [HNOI2016] 大数。
方差可以考虑先乘 \(n^2\),得到 \((n\sum x^2)-(\sum x)^2\)。
有时一些问题在 01 序列上有更优的复杂度,考虑可以将一般问题转换为 01 序列问题,比如二分,二进制拆分等。P2824 [HEOI2016/TJOI2016] 排序。
对每个 \(a_i\) 维护一个上一次出现的位置 \(last_i\) 可能有意想不到的结果。P4113 [HEOI2012] 采花。
可以转变思维,考虑点能对那些询问产生贡献,而不是有哪些点对该询问产生贡献。
将贡献的公式写出来并进行一些简化是个好习惯,然后对其考虑如何维护。P3760 [TJOI2017] 异或和。
要考虑 or、xor、and 之间的转换。
我们可以用颜色来维护一些东西,比如颜色相同代表有边,这样对于某些操作就十分方便。P7735 [NOI2021] 轻重边
不要忘了倍增的复杂度是 \(O(\log n)\) 的,所以有时暴力复杂度是对的。P4587 [FJOI2016] 神秘数。
做一个题时,可以先考虑题目的性质,然后解决一些前提问题,比如如何考虑判断合法,如何快速计算一个点的值等。
一定要将答案的式子写出来。
0/1 线性规划:P4322 [JSOI2016] 最佳团体。直接二分答案然后判断即可。
找到一个在满足最优性下等价的宽松性质。P3287 [SCOI2014] 方伯伯的玉米田,P3586 [POI2015] LOG
一对点联通是否或者是其它的询问,如果可以转化为一些信息是否相同(比如并查集中点 \(x\) 的根),并且这些信息可以比较容易的维护,我们可以考虑哈希,进行快速比较。P8026 [ONTAK2015] Bajtocja。
如果一道题不会,可以哈希和随机化乱搞,能骗多少分骗多少分。
哈希也可以维护 LCP 之类的东西,虽然查询复杂度比后缀数组劣,但是支持的操作更多。
一个范围很大的题目或无法快速判断的题目,考虑可以随机化。
随机数据下一些做法的复杂度会下降。
\(\gcd(x,y)=\gcd(x,y-x)\)。
对一个序列求最优子区间,可以单调递增的枚举右端点,动态维护每个左节点的值。P3582 [POI2015] KIN
二进制分组
可以对时间轴分块。
严格大于一半的众数,可以用摩尔投票法计算,然后再判断一下即可。
如果题目有限制,我们可以先确保一个限制然后再考虑其他限制。
枚举中间点。
可以将一些限制分开考虑,然后再合并起来。P4065 [JXOI2017] 颜色
分类讨论。
要仔细研究题目给出的性质,要推导出一个强性质用于求解。
求满足一些限制的合法方案数时,要找到一个方法来快速判断一个解是否合法,然后根据这个方法的性质来求合法方案数。
一般图的问题可以先考虑特殊图上如何求解,比如树,基环树,稀疏图,链,菊花图,对点的度数进行根号分治等。
对度数/时间/数的大小进行根号分治。
可以离线,将修改/询问放在一起统一计算。
压位,优化一个 \(w\)(计算机字长)。
\(O(\sum_{i=1}^{n}\frac{n}{i})\) 大概是 \(O(n\log n)\) 。
拆分区间的思想,将一个区间拆成 \(\log n\) 或 \(\sqrt{n}\) 个子区间,然后用数据结构维护,比如线段树、树状数组、分块。P4215 踩气球。
拓展欧拉定理 P3747 [六省联考 2017] 相逢是问候 P3934 [Ynoi2016] 炸脖龙 I
树上路径上的 k 大点权 P2633 Count on a tree
回退数据结构,一般配合线段树分治使用。
用 \(2^i\) 的段分解成两个 \(2^{i-1}\) 的段,用来优化复杂度,P3295 [SCOI2016] 萌萌哒。
多路并行:P2048 [NOI2010] 超级钢琴,P5283 [十二省联考 2019] 异或粽子。
动态规划
将一个 dp 式写出来并进行一些简化是个好习惯。
用矩阵维护转移:P7739 [NOI2021] 密码箱。
P4063 [JXOI2017] 数列:考虑相邻两个点的取值范围就可以得到结论了。
P8820 [CSP-S 2022] 数据传输:\(k=1\) 直接走即可,\(k=2\) 不会离开 \(x\) 到 \(y\) 的链,\(k=3\) 最多只会到达链上的点的相邻点,可以用矩阵维护 dp 转移。
P3750 [六省联考 2017] 分手是祝愿 一眼看很迷茫,先考虑 \(k=n\) 时的情况,操作顺序不会对结果产生影响。设最后一个亮的位置是 \(x\),若操作了 \(\ge x\) 的位置 \(y\),且 \(y\) 是 \(x\) 的倍数,显然答案只会变劣,所以我们只能操作 \(x\),然后递归下去,所以最优操作是唯一的,因此如果我们操作了一个不再最优操作的位置,我们需要将其在操作一边,所以当前局面的答案为 \(f_{i}\),有 \(f_{i}=1+\frac{f_{i-1}i}{n}+\frac{(n-i)f_{i+1}}{n}\),dp 一下即可。
P4517 [JSOI2018] 防御网络 考虑边的贡献,然后对边是否为割边进行分类讨论即可。
P3311 [SDOI2014] 数数:数位 dp,将在 AC 自动机的位置作为 dp 信息。
在 data structure 的全局平衡二叉树部分。
一般是用矩阵维护 dp 转移,线段树之类的直接维护 dp 值。
P5772 [JSOI2016] 位运算:由于 dp 式具有周期性(大小为 \(|S|\))所以我们可以用矩阵快速转移,至于矩阵系数我们可以用 \(2^n\) 次 dp 来维护。
P3736 [HAOI2016] 字符合并,需要精细实现,区间长度为 \(x\) 的 \([l,r]\),经过化简后变为长度为 \(x\bmod m+[x\ge m]\),然后枚举最后一个 0/1 是由那个后缀化简得到的,复杂度明显小于 \(O(n^32^k)\)。
P4072 [SDOI2016] 征途,复杂度 \(O(nm)\)。
一般函数是一个下凹壳后上凸壳,考虑二分斜率,每划分一个区间就减去一个操作费。
P4072 [SDOI2016] 征途,\(\sum x^2\) 是一个下凹壳,所以可以 wqs 二分。复杂度 \(O(n\log V)\)。
P4383 [八省联考 2018] 林克卡特树:先 wqs 二分,然后直接 dp 即可。
P5503 [JSOI2016] 灯塔 可以放在二维平面上考虑,由于 sqrt 的增长越来越小所以有决策单调性。
P3290 [SCOI2016] 围棋 容斥一下求不合法的方案数。维护 \((S,p1,p2)\) 表示最后一行和模板的第二行匹配了 \(p2\) 个,倒数第二行和模板第一行匹配了 \(p1\) 个的方案数,使得没有一个位置和模板串匹配。
将内层 dp 值作为外层 dp 的信息:P4590 [TJOI2018] 游园会。
P8290 [省选联考 2022] 填树:求出最小值为 \(v\) 的方案数,显然最大值最多为 \(v+k\),我们先求出 \([v,v+k]\) 的解的个数,然后求出 \([v+1,v+k]\) 的解的个数,两者相减就得出最小值为 \(v\) 的方案数,由于 \(v\) 的范围很大,并且方案数和权值和在一段区间内是可以用多项式表达的,可以考虑用拉格朗日插值求解,按 \(l_i\) 和 \(r_i\) 分段求解即可。
P7605 [THUPC2021] 小 E 爱消除:直接暴力 dp,分成区间 dp 和 匹配两段的 dp,复杂度很高但是常数特别小且许多 dp 值并不会枚举到,所以我们可以直接记忆化 dp 就行。
P6885 [COCI2016-2017#3] Zoltan:显然最优解是由两个不相交的上升子序列和下降子序列合并形成的,在推敲一下,上升子序列一定在下降子序列之前,于是我们解决了第一问,由于求的是子序列个数的总和,所以我们 dp 时记录一下方案数即可。
P6708 [CCC2020] Josh's Double Bacon Deluxe:逆序 dp 考虑一下拿一个汉堡对后面的影响即可。
P6647 [CCC2019] Tourism:\(t=\lceil\frac{n}{k}\rceil\),由于有时间和区间大小限制所以 wqs 二分行不通,我们对每划分一个区间就加上一个很大的手续费 \(\infty\),做只考虑 \(k\) 的 dp,就会使划分段数尽量少,也就是 \(\lceil\frac{n}{k}\rceil\)!线段树维护即可,复杂度线性对数。
P6371 [COCI2006-2007#6] V:考虑根号分治,\(X\le \sqrt{B}\) 时直接数位 dp,复杂度 \(O(X\log_{10}B)\),否则直接暴力枚举 \(X\) 的倍数即可,复杂度 \(O(\frac{B}{X})\)。
P6287 [COCI2016-2017#1] Mag:考虑全 1 串和只有 一个 \(>1\) 的串。
P5574 [CmdOI2019] 任务分配问题,区间逆序对是满足四边形不等式的,所以我们可以直接用决策单调性,但是区间逆序对是没有线性对数做法,所以我们只能用分块或莫队之类的,分块显然会超时,如果我们用分治做决策单调性,莫队的复杂度是有保障的,端点移动 \(O(n\log n)\) 次,所以复杂度是 \(O(nd\log^2 n)\),\(k\) 似乎可以开大,因为区间逆序对也可以 wqs 二分。
P5307 [COCI2018-2019#6] Mobitel:如何 dp 式很难直接维护,我们可以寻找一个等价的 dp 状态表示。比如乘积为 \(x\),变为还需要 \(n/x\) 才合法,根据整除分块的理论,\(n/x\) 只有 \(O(\sqrt{n})\) 个。
string
子序列自动机
KMP 和 Border、z函数
P3193 [HNOI2008] GT考试:KMP 维护匹配,然后用矩阵维护 dp 快速转移。
P3502 [POI2010] CHO-Hamsters:\(n\) 次 KMP 计算转移系数,然后矩阵快速幂即可。
P3546 [POI2012] PRE-Prefixuffix 。
P3290 [SCOI2016] 围棋:把 KMP 信息作为轮廓线 dp 的信息。
SA、SAM、后缀树
P1117 [NOI2016] 优秀的拆分,考虑统计 AA 的结尾为 \(i\) 的方案数 \(F_{i}\),BB 的开头为 \(i\) 的方案数 \(G_{i}\),答案为 \(\sum_{i}F_iG_{i+1}\),然后我们暴力枚举长度 \(len\),将 \(len|i\) 的位置 \(i\) 称为关键点,显然一个 AA 一定会经过两个相邻的关键点,设其为 \(i\),\(j\),两个 A 的分界点在 \([i,j-1]\) 中,设为 \(p\),则 \([i,p]=[j,j+p-i]\),然后 \([p+1,j]=[p-len+1,i-1]\)。直接 \(O(1)\) 得到 \(i,j\) 的 \(\operatorname{LCP}\) 和 \(\operatorname{LCS}\) 即可计算合法的 \(p\) 的个数,复杂度是调和级数 \(O(n\log n)\)。
P3181 [HAOI2016] 找相同字符,可以 SA 和 SAM,但是 SA 好想一些。
P2336 [SCOI2012] 喵星球上的点名,首先对于一个喵的性和名用一个不属于 a 至 z 的字符连接起来。
SA做法就是将所有喵的性名和询问连起来并用SA一遍求出,然后就是对一段区间求不同数字的出现个数,可以 \(O(n\log n)\) 求解,类似 HH 的项链。- 对于
SAM做法,就是将所有喵的性名扔到自动机中,用线段树合并(因为信息不是 \(\operatorname{endpos}\))维护每个节点代表的字符串是哪些喵的姓名中。
- 将所有串放在一起跑
SA,二分答案 \(p\),然后判断在后缀数组上是否有一段区间 \([l,r]\) 使得 \(LCP\) 大于 \(p\),且包含所有串的的一个后缀,可以 two-pointer \(O(n)\) check。复杂度 \(O(m\log m)\)。 - 放在自动机上,然后线段树合并大力维护即可。复杂度 \(O(m\log m)\)。
把字符串反转并放在原串后面,统计一个贡献。P9482 [NOI2023] 字符串
P3181 [HAOI2016] 找相同字符,可以建出 height 数组,然后从大到小合并并统计即可,还可以用 sam 但是由于没啥意义就放在 SA 中了。
可以配合线段树合并维护 endpos 的具体信息,可以配合倍增一个子串代表的节点。
P4094 [HEOI2016/TJOI2016] 字符串:倍增求出 \([c,d]\) 在 SAM 的位置 \(p\),然后线段树合并维护 endpos 集合,然后二分答案、线段树上 \(O(\log n)\) check 即可。
P4384 [八省联考 2018] 制胡窜 大力分类讨论,考场没时间可以写较劣的做法。
P2408 不同子串个数:求一个字符串本质不同子串个数。
后缀树就是反串放在 SAM 上的 fail 树,可以 \(O(n\log n)-O(1)\) 的求 LCP,用 \(O(n)-O(1)\) 的 RMQ 可以做到 \(O(n\sum)\) 的预处理(瓶颈是 SAM 构建的复杂度),\(O(1)\) 求解。并且后缀树可以维护一些前缀包含问题,将其变成变成图论问题,然后求解。P5284 [十二省联考 2019] 字符串问题,后缀树上缩点、dp,还要对后缀树上的边重构一下。
P3346 [ZJOI2015] 诸神眷顾的幻想乡:广义 SAM,首先从所有叶子遍历一定能将所有路径包含,其次由于叶子只有 20 个所以暴力搜索即可。
P4248 [AHOI2013] 差异:无脑 SA。
P4081 [USACO17DEC] Standing Out from the Herd P:
- 广义
SAM:统计每个节点的在哪些串出现,然后再将串串放上去跑一边即可。 SA:考虑每个后缀和其它串的 \(\operatorname{LCP}\) 最大值 \(v\),则该后缀的贡献为该后缀长度减去 \(v\),复杂度 \(O(n\log n)\),十分好写。
P5028 Annihilate:大力 SA,对每个串正向/反向扫一下 height 数组即可。
P9664 [ICPC2021 Macao R] LCS Spanning Tree:SA 后直接求生成树即可。
P7769 「CGOI-1」大师选徒,设 \(b_{i}=-a_{i}\),然后 \(b_{i}=a_{i}-s\),然后差分消除 \(s\) 的影响,然后求 SA,判断就很容易了。
P7409 SvT:SA 后可以类似品酒大会用并查集计算,复杂度 \(O(n\log n+(\sum t)\alpha(n))\),但是并查集有些大材小用,直接单调栈可以做到线性。
P8368 [LNOI2022] 串:十分妙的题,并不是什么字符串重工业题。显然若 \(T_{i}=[l,r]\),则 \(T_{i-1}=[l-1,r-2]\),若存在最大的 \(x\) 使得 \([x,y]=[l-1,r-2]\),\(x>l-1\),则 \(T_{i=1}=[x,y]\)。如果最优解中不存在这种情况的答案为 \(\lfloor\frac{n}{2}\rfloor\),否则设 \([x,y]=[l,r]\),则我们从 \([l,r]\) 一直向左跳,当左端点到 \(x\) 返回 \(l\) 即可,一定会跳到空串,然后计算 \([l,r]\) 右边的部分,此时答案为 \((r-l+1)+\lfloor\frac{n-r}{2}\rfloor\),建立 SAM 维护即可,对每个节点维护 endpos 的最小值和大小即可,复杂度 \(O(\sum |S|)\)。
AC 自动机、Trie 树
多串问题一般是用 AC 自动机维护,只有涉及到本质不同子串、endpos 才会用 SAM 和广义 SAM、SA 等。
P3735 [HAOI2017] 字符串 多串匹配还得是 AC 自动机将模板串和匹配串的正反串放在 AC 自动机上匹配即可。
P2292 [HNOI2004] L 语言:直接构造自动机然后 dp 即可,由于模板串长度只有 \(20\),可以压在一个 int 中,询问复杂度优化到 \(O(|t|)\)。
P2444 [POI2000] 病毒,构造病毒串的 AC 自动机,其中一些点不允许经过,求从 \(1\) 出发是否能到达一个环即可。
P2536 [AHOI2005] 病毒检测把询问放在一起建立 AC 自动机,然后将病毒模版片段放上去跑即可,加上记忆化即可保证复杂度。
P2414 [NOI2011] 阿狸的打字机:询问可以换一个表达: \(x\) 代表的字符串是多少个 \(y\) 代表的字符串的前缀的后缀?对 Trie 建出自动机和它的 fail 树,字符串 \(s\) 是 \(t\) 的后缀当且仅当 fail 树上 \(s\) 是 \(t\) 的祖先,放在 dfs 序上就是 \(s\) 包含 \(t\)。所有我们将询问 \((x,y)\) 挂到 \(y\) 处统计,然后遍历 Trie 树并用 dfs 序维护即可,复杂度 \(O(n\sum+n\log n)\)。
P3311 [SDOI2014] 数数:数位 dp,将在 AC 自动机的位置作为 dp 信息。
P5231 [JSOI2012] 玄武密码:对询问串建立 AC 自动机,将母串放在上面跑即可,求出节点 \(i\) 代表的字符串是否是母串的子串。可以无脑 SAM,但是没有意思。
P5840 [COCI2015] Divljak:对 \(S\) 构建 AC 自动机,然后将 \(T\) 中的字符串放上去匹配,然后用线段树合并维护是 \(T_i\) 的子串的集合 \(\{T_i\}\)。
P6125 [JSOI2009] 有趣的游戏,根据 AC 自动机构建转移方程,由于有后效性,所以需要 Guass 消元。
P8451 [LSOT-1] Crosspain:将问题离线求出操作树和 \(S\) 的 AC 自动机,然后 dfs 操作树即可。
Manacher、回文自动机
回文串最多只会有 \(n\) 个·。
P9482 [NOI2023] 字符串:主要是除去重复贡献,即将回文串的贡献去掉,直接将贡献放在二维平面上统计即可。
P3649 [APIO2014] 回文串:直接建立回文自动机即可。
P4287 [SHOI2011] 双倍回文:Manacher计算以 \(i\) 开始/结尾的回文串个数。
P5685 [JSOI2013] 快乐的 JYY,建立两个 PAM,然后 dfs 即可。
Lydon
math
容斥
树上统计连通块方案数有一个容斥是 \(|V|=|E|+1\),即强制包含一个点的方案数减去强制包含一个边的方案数。
正难则反。\(|P|=|S|-|\overline{P}|\)。
https://www.luogu.com.cn/problem/P5366。
P3349 [ZJOI2016] 小星星:恰好和子集之间的转化。
二项式反演
鸽笼原理:P7738 [NOI2021] 量子通信
[P4478 [BJWC2018] 上学路线 P3734 [HAOI2017] 方案数。带容斥系数的 dp。
P3813 [FJOI2017] 矩阵填数:并不是取反容斥,而是 \(\le v\) 和 \(< v\) 的容斥。
斯特林数
P4091 [HEOI2016/TJOI2016] 求和 大力推导即可。
矩阵乘法
一般用于优化 DP。
有时转移矩阵比较特殊,我们可以再矩乘时只转移有意义的点,优化常数。P3781 [SDOI2017] 切树游戏。
FWT
and、or、xor 卷积。
行列式、matrix-tree 定理、LGV 引理
交换一行,行列式的值 \(x\) 变为 \(-x\)。
matrix-tree 定理:求的是所以生成树的边权乘积的和:度数矩阵减去邻接矩阵的行列式,可以带权,可以求有向图的生成树(内向、外向)。
- \(D_{i,i}=\sum_{j}A_{j,i}\) 是外向树。
- \(D_{i,i}=\sum_{j}A_{i,j}\) 是内向树。
- 删去 \(k\) 行 \(k\) 列代表的是以 \(k\) 为根。
复杂度 \(O(n^3)\)。
P5296 [北京省选集训2019] 生成树计数,边带权的 matrix-tree,边权可以是生成函数。
LGV 引理:求的是起点集合 \(S=\{s_1,s_2,\dots,s_n\}\) 到终点集合 \(T=\{t_1,t_2,\dots,t_n\}\) 的不相交路径数(一个方案带权 \(-1^{N(p)}\),表示 \(i\to p_i\),\(N(p)\) 表示排列 \(p\) 的逆序对数)。\(A_{i,j}\) 表示从 \(s_i\) 到 \(t_j\) 的路径上边权乘积的和,\(\det(A)\) 即为答案,当然也可以边带权。
置换
一个置换可以写成循环的乘积。一般和置换有关的题可以从这里作为切入点。
我们可以对循环的大小进行根号分治,或者将大小相同的循环放在一起计算,复杂度有一个 \(\sqrt{n}\)。P8338 [AHOI2022] 排列。
burnside 和 polya 定理:用于计算等价类的个数。对等价关系构造置换群(自反性、对称性、传递性),一个置换 \(f\) 的不动点为 \(C(f)\),则等价类一共有 \(C(f)\) 的平均数个,在考虑染色和循环分解就得到 polya 定理咧。
杜教筛
\(S_{i}=\sum_{j\le i}f_{i}\)。
inline LL MU(LL n){
if(n<N)return mu[n];if(Mu.count(n))return Mu[n];LL ans=1;
for(LL i=2,j;i<=n;i=j+1)j=n/(n/i),ans-=(LL)MU(n/i)*(j-i+1);
return Mu[n]=ans;
}
inline LL PHI(LL n){
if(n<N)return phi[n];if(Phi.count(n))return Phi[n];LL ans=(LL)n*(n+1)/2;
for(LL i=2,j;i<=n;i=j+1)j=n/(n/i),ans-=(LL)PHI(n/i)*(j-i+1);
return Phi[n]=ans;
}
graph
最短路
对于点权最短路,若当前枚举到了 \(u\),存在边 \(u\to v\),则 \(dis[v]=dis[u]+val[v]\),并扔到堆中,以后不对它进行松弛,因为 \(v\) 一定是由其 \(dis\) 最小的前继 \(u\) 转移而来,由于每个点只会被转移一次,所以复杂度是严格 \(O(n\log n+m)\),而不是 \(O(m\log n)\),因为每个点只会且仅松弛一次。
P7214 [JOISC2020] 治療計画 把时间-村民的图画出来,一个操作可以看成一个横着的直角三角形,显然 \([1,?]\) 和 \([?,n]\) 的方案必须有,不然 \(1\) 和 \(n\) 永远都是感染状态,然后对于图像中有交的操作连边,一个合法方案一定使得一个 \([1,?]\) 和 \([?,n]\) 联通,也就是一个点权最短路,用线段树优化一下,复杂度是 \(O(n\log n)\)。
P3783 [SDOI2017] 天才黑客:考虑前后缀优化,然后用字典树排序统计顺序以及快速求解 LCP。
同余最短路
Two-Sat
P3825 [NOI2017] 游戏 部分 3-sat 问题,直接 \(O(2^k)\) 枚举,转变为 2-sat 问题。
P6378 [PA2010] Riddle 前后缀优化建图。
P5332 [JSOI2019] 精准预测,利用了 two-sat 的定义,然后用分块和 bitset 优化。
线段树优化
由一个点向一段区间连边(\(O(n)\to O(\log n)\)),区间向区间连边(\(O(n^2)\to O(\log n)\)),边的本质相同。
前后缀优化建图
一个区间 \([l,r]\),点 \(i\in [l,r]\) 向 \([l,i-1]\) 和 \([i+1,r]\) 连边。
P6378 [PA2010] Riddle 前后缀优化建图,然后 2-sat 即可。
字典树优化建图
一般是和字符串前缀匹配有关的问题。
最小路径覆盖、最小链覆盖
给一个 DAG,求最少要用多少条路径或链才能将整个 DAG 覆盖。
Dilworth's Theorem
模拟费用流
直接跑费用流的复杂度过大,我们可以用数据结构模拟费用流的过程。
二分图
二分图最大独立集:P2825 [HEOI2016/TJOI2016] 游戏。
网络流
重点在于建边及其优化。
按照质因数个数构造二分图,并求解:P3736 [HAOI2016] 字符合并。
最小割树:一个图最多只有 \(n\) 个最小割,我们可以跑 \(n\) 次最小割求出一个最小割树,满足两个点的最小割为两个之间路径边权的最小值。我们可以先求 \(x\) 和 \(y\) 的最小割 \(z\),并划分为两个集合 \(S_x\) 和 \(S_y\),然后连边 \((x,y,z)\),然后递归求解 \(S_x\) 和 \(S_y\) 的最小割树。P4123 [CQOI2016] 不同的最小割。
P5458 [BJOI2016] 水晶 无论是 a 共振还是 b 共振都会包含一个带有能量源的点,先对三维平面化简成二维平面,然后按 \(\bmod 3\) 的值分类并建立图跑最小割即可,可以将代价乘十避免 double 运算,最后在除去。
data structure
线段树
可以维护许多可合并的信息。
P3309 [SDOI2014] 向量集 线段树的一个节点维护一个结点,对于一个节点,如果区间内的向量均已加入后在合并儿子的凸壳,维护信息的复杂度为 \(O(n\log n)\),询问是对于一个节点直接二分即可,复杂度 \(O(\log^2n)\)。
线段树合并可以将增加和删除操作变成增加或删除加上撤销,复杂度加上一个 \(\log\)。P3250 [HNOI2016] 网络。\(O(n\log^3n)\)。
可以用它维护 DP,也可以用来跑最短路,特别是点权最短路,每个点仅松弛一次,
P7214 [JOISC2020] 治療計画 把时间-村民的图画出来,一个操作可以看成一个横着的直角三角形,显然 \([1,?]\) 和 \([?,n]\) 的方案必须有,不然 \(1\) 和 \(n\) 永远都是感染状态,然后对于图像中有交的操作连边,一个合法方案一定使得一个 \([1,?]\) 和 \([?,n]\) 联通,也就是一个点权最短路,用线段树优化一下,复杂度是 \(O(n\log n)\)。
[P1848 USACO12OPEN Bookshelf G 优化 DP。
可以优化建边。
主席树可以有效维护整个时间轴中每个序列的状态。
线段树合并也可以维护dp,
P4198 楼房重建 合并方式是 \(O(\log n)\) 的,所以我们做题也不是不可以用线段树维护信息。
精细实现的化,动态李超树的空间复杂度是 \(O(min(n,m))\) 的,\(m\) 为操作次数,\(n\) 为李超树的大小,你可以认为空间复杂度上复杂度比时间复杂度少一个 \(\log\)。
P4069 [SDOI2016] 游戏,由于插入的是一个等差数列,也就是一个线段,所以我们可以用李超线段树维护,修改的复杂度为 \(O(\log^3n)\),询问复杂度为 \(O(\log^2n)\)。
P3747 [六省联考 2017] 相逢是问候,每个数最多只会操作 \(O(\log c)\) 次就不变了,所以我们可以在线段树上暴力修改,加上一些特判(区间的所有数是否进行了 \(O(\log c)\) 次操作,如果是那么修改无意义)即可保证复杂度。
P5210 [ZJOI2017] 线段树:首先我们要知道在广义线段树中 \(S_{[l,r]}\) 代表什么。设 \(leaf_i\) 表示广义线段树中代表 \([i,i]\) 的节点。显然 \(leaf_l\) 的深度最小的满足 \([l_{fa_l},r_{fa_l}]\subseteq [l,r]\) 的祖先 \(fa_l\) 一定在 \(S_{l,r}\) 中,并且是左端点最小的节点,\(fa_r\) 类似,是右端点最大的节点。然后设 \(t\) 表示 \(fa_l\) 和 \(fa_r\) 的 \(\operatorname{lca}\),那么从 \(fa_l\) 到 \(t\) 的路径上,若 \(x\) 是父亲 \(y\) 的左儿子则 \(x\) 的兄弟也在 \(S_{l,r}\) 中(\(x\ne t\),\(y\ne t\)),\(fa_r\) 到 \(t\) 的情况是对称的。知道了 \(S_{l,r}\) 是什么后,我们考虑如何求解。首先我们要维护一些信息使得我们可以 \(O(1)\) 的求出 \(S_{l,r}\) 内的节点到路径 \(fa_l\to fa_r\) 中一个节点的距离的和,维护信息是平凡的,因为我们所需的信息可以树上差分,所以我们可以 \(O(n)\) 预处理。然后我们求出 \(fa_l\to u\) 和 \(fa_r\to u\) 的路径的第一个交点 \(e\),显然 \(S_{l,r}\) 的绝大多数点到 \(u\) 的路径都会经过 \(e\),所以我们求出 \(S_{l,r}\) 到 \(e\) 的距离然后加上 \(e\) 到 \(u\) 的距离乘上 \(|S_{l,r}|\) 即可,当 \(u\) 在某个节点 \(x\) 的子树时(\(x\in S_{l,r},x\ne fa_l,x\ne fa_r\)) \(x\to u\) 的路径并不会经过 \(e\),特判一下即可。
P4559 [JSOI2018] 列队:线段树上二分位置即可。
P4477 [BJWC2018] 基础匹配算法练习题:将 A 排序后匹配的是一个前缀,然后我们发现匹配信息是可以合并的,所以我们可以直接用线段树维护即可。
树状数组
树状数组上倍增,单次复杂度是 \(O(\log n)\) P6619 [省选联考 2020 A/B 卷] 冰火战士。
原理是树状数组上节点 \(i\) 表示的是 \(i-\operatorname{lowbit}(i)+1\sim i\) 的信息和。
inline void ask(...){
int now=0;
for(int i=26;~i;i--)if(now+(1<<i)<=n){
int t=now+(1<<i);
if(...){...;now=t;}
else{...}
}
}
分块
一道题目无法用 poly 的数据结构维护时可以考虑分块,分块的方式多种多样,可以对序列长度分块,也可以对值域分块,还可以对时间分块。
P5332 [JSOI2019] 精准预测,利用了 two-sat 的定义,然后用分块和 bitset 优化。
斯坦纳树
求一个图 \((V,E)\) 的边权最小的导出子图 \((V',E')\) 使得 \(x\in S\) 点连通。
字典树
krustral 重构树
将 krustral 的过程用一颗二叉树表示出来,用于维护瓶颈集合。P4768 [NOI2018] 归程。
cdq分治
将问题分而治之。只考虑一边对另一边的贡献,集中处理。
P4093 [HEOI2016/TJOI2016] 序列。第一眼很迷茫,但是仔细考虑并不难。先考虑在最优解中两个相邻的数 \(x\)、\(y\) 需要满足什么条件:\(\max a_x\le a_y\)、\(a_x\le \min a_y\)。也就是一个三维偏序问题,cdq 分治计算即可。
P3755 [CQOI2017] 老C的任务:考虑差分然后 cdq 分治统计贡献即可。
虚树
P4426 [HNOI/AHOI2018] 毒瘤 优化 dfs 的复杂度,对于重复遍历的边压缩一下即可。
P7737 [NOI2021] 庆典,若 \(x\to z\) 且 \(y\to z\),则存在 \(x\to y\) 或 \(y\to x\),进一步的若 \(E(x)\cap E(y)\) 则 \(E(x)\subseteq E(y)\) 或 \(E(y)\subseteq E(x)\),也就是有一个树 \((V',E')\) 等价于原图 \((V,E)\),\(E'\subseteq E\),可以考虑拓扑排序求得,然后对起点终点、\(k\) 条边求解即可,然后用虚树优化一下即可做到 \(O(n+m+qk\log n)\)。
圆方树
图上的路径问题可以考虑圆方树,要考虑一个强连通分量的影响,以及一些必经点。
P4606 [SDOI2018] 战略游戏 求一些点之间的必经点集合之并,对于一对点 \((u,v)\),其圆方树上简单路径的圆点就是必经点。
P3180 [HAOI2016] 地图 画一画图可得点 \(x\) 可达的点为以 1 为根的圆方树中的 \(x\) 的子树。然后可以放在序列中做莫队,也可以直接启发式合并,还可以线段树合并。
启发式合并
将小的暴力枚举并合并到大的上,由于小的大小乘二,所以只会有 \(O(n\log n)\) 次合并操作。
P3201 [HNOI2009] 梦幻布丁 启发式合并维护每个颜色的极长连续段,用 set 维护复杂度 \(O(n\log^2n)\)。
点分树和点分治
统计树上路径信息,点分树是将点分治的过程用树记录下,可以一定意义下多次查询、修改,树高是 \(\log n\) 的,所以直接跳父亲的复杂度是正确的。
P4075 [SDOI2016] 模式字符串,用哈希维护一段路径前缀匹配以及后缀匹配即可,然后统计子树 \(v\) 时先除去所以的后缀匹配路径在统计有多少个前缀匹配即可。
LCT
求 lca 可以用两次 access。可以用来动态维护树或不删边的图的连通性,一般还需要用其他的数据结构维护具体信息, LCT 上可以维护儿子信息,还可以一定程度上维护虚儿子的信息。
可以配合线段树分治来维护任意一个图的连通性。
可以动态维护 sam 的 fail 树,P5212 SubString。
对操作/形态进行差分,然后用 LCT 维护动态树,还要用到虚点的技巧:P3348 [ZJOI2016] 大森林。
全局平衡二叉树(DDP)
一般用来优化掉树剖的一个 \(\log\),对于每个重链建立二叉树,使得重链上也满足向上跳一次大小乘二的性质,这要从任意一个点向上跳的复杂度是 \(O(\log n)\) ,其实是 LCT 的静态版本,满足树剖的性质。维护矩阵的复杂度(DDP)仅为 \(\log n\),而不是 \(\log^2n\)。
凸包
动态凸包(只增) P2497 [SDOI2012] 基站建设
K 远点对:P4357 [CQOI2016] K 远点对,每次取最远的两个点并将其它点到这两个点的距离加入堆中,然后删去这两个点,重复 K 次就一定能求出 K 远点对。
线性基
在异或意义下,最多只需 \(n\) 个不同的数就可以表示出 \(2^n-1\) 内的所有数。P5556 圣剑护符。
可以求异或最大值、最小值。



 浙公网安备 33010602011771号
浙公网安备 33010602011771号