端点星 3-copute

端点星 3.测试

T1 算数（copute）

【题目描述】
栓柱在数学课上学习了完全立方数，老师想考验一下栓柱的算术能力，
单纯计算平方与立方对栓柱来说太过简单，于是老师随手写了𝑇个数字，他
希望栓柱能计算出这个数是否是两个正整数的完全立方数的差。
由于计算量太大，老师又规定这个𝑇个数字都为质数。


看到这题首先想到的便是预处理立方差暴力求解，但是复杂度根本过不
了，于是便开始优化：

• 观察到数是质数，考虑立方差公式
	a^3 − 𝑏^3 = (𝑎−𝑏) (a^2+ab+b^2)
显然，𝑎 − 𝑏 = 1，说明𝑎, 𝑏是两个相邻的正整数，得出
𝑎^2 + ab + 𝑏^2 = (𝑎 − 𝑏) ^ 2 + 3𝑎b = 1 + 3𝑎b
所以在所有的询问中，是立方差的质数必然是由两个相邻正整数
𝑎, 𝑏的1 + 3ab计算得到的。
故预处理所有的1 + 3𝑎b，注意到𝑝 ≤ 10^12，所以预处理到一个𝑎 =
59000左右的数即可，又因为𝑇 ≤ 100，可以预处理完成后直接暴力
查询。
复杂度𝑂(max (𝑎) 𝑇)
• 好，T1就这么被切了（好像有点水）

---

T2 正方形覆盖（rectan）

【题目描述】
翠花研究了矩形覆盖问题后，自己发明了一种矩形覆盖游戏，游戏规则
如下：
直角坐标系平面上有𝑛𝑛个点，每个点的坐标均是正整数坐标(𝑥𝑖, 𝑦𝑖)，翠花
想用𝐾个平行于坐标轴的正方形覆盖所有的点，每个正方形的边长都为𝐿，翠
花想知道，用这𝐾个正方形覆盖所有点的最小的𝐿是多大（位于正
方形边界的点也看作被覆盖）。
一开始想了将近15分钟，不会做（好像是模拟），然后就放弃了，赛
后看题解才明白（就是模拟。。。再加上二分。。。）：

• 观察到𝐾 ≤ 3，还有𝑦𝑖 = 0，可以分类讨论，由部分拓展到全局。
• 𝐾 = 1时，L = max(x(max)-x(min),y(max)-y(min)).
• 𝑦𝑖 = 0时，弱化为一维线段覆盖，这种同时满足最大最小的问题
显然是一种二分操作。二分𝐿，把𝑥从小到大排序，然后从左到右
按𝐾覆盖点，第𝑖次覆盖从第𝑖 − 1次覆盖到的最后一个点的下一个
点开始。直到二分到最小的𝐿.
• 𝐾 = 2
• 先将问题缩小范围，找到一个矩形，能把所有的点恰好覆盖，我
们的正方形显然就在这个矩形内部，矩形的长为x(max)-x(min),高
为𝑦(max)-y(min)。
• 问题性质不变，仍然二分𝐿，注意到两个正方形一定是这两种位
置其中一种。 两个正方形都在对角，否则就会有在矩形边界上的点
不被覆盖到。

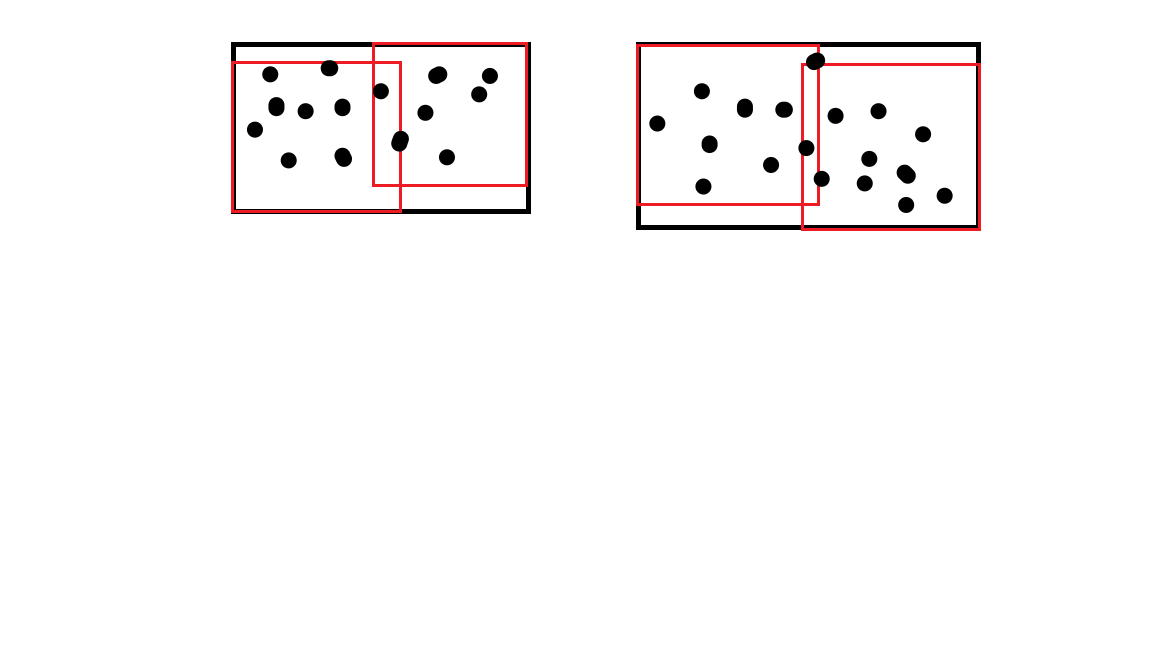
所以我们只需每次二分都遍历所有点，判断是否被完全覆
盖即可。
复杂度为𝑂(2𝑁 lg(2 ∗ 106)
好吧，我太菜了，没看懂题解代码。。。但大概是这个意思

---

T3 走格子（block）

【题目描述】
翠花和栓柱正在玩一个叫做走格子的游戏，他们在地上画了一个(𝑛 +1) ∗ (𝑚 + 1)的网格，每个格子中有一个整数𝑎(𝑖,𝑗)。
栓柱规定，位于坐标(𝑥, 𝑦)的格子上的数有
	𝑎(𝑥,𝑦) = 𝑎(𝑥−1,𝑦) + 𝑎(𝑥,𝑦−1)[𝑥, 𝑦 > 0]
翠花规定，对于任意的0 ≤ 𝑖 ≤ 𝑛, 0 ≤ 𝑗 ≤ 𝑚，有
	𝑎(𝑖，0) = 𝑎(0,𝑗) = 1
在游戏过程中，每个人只能从网格的左上角(0,0)出发，一直走到格子的
右下角(𝑛, 𝑚)，每次移动只能向上下左右四个方向移动，也就是说如果他们
位于坐标为(𝑥, 𝑦)的格子上，他们只能移动到(𝑥 − 1, 𝑦), (𝑥, 𝑦 − 1), (𝑥 + 1, 𝑦)和
(𝑥, 𝑦 + 1)这四个格子上，而且不能走出整个网格，他们每到达一个方格就会
取得这个格子上的整数作为得分，由于厌倦了“方格取数”类的问题，他们
想知道怎样走能够最小化总得分(初始状态得分为1)。

看到这个题，我首先想到的是dfs，但是发现假了，于是题目中给出
许多状态，这不就是dp了吗，好，20min打出20分暴力。。。然后就
不会优化了。看了题解后才明白：

• 观察方格的核心性质𝑎（𝑥,𝑦） = 𝑎（𝑥−1,𝑦 + 𝑎 𝑥,𝑦−1） ，显
然是一个旋转45°的杨辉三角，如图。

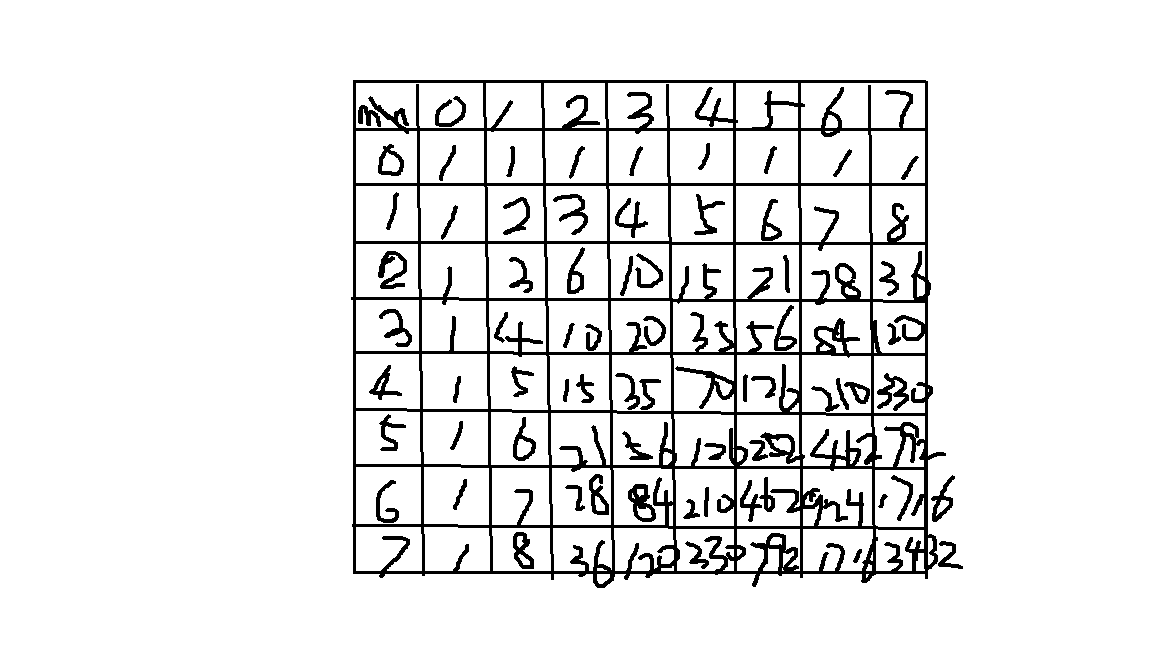
所以对于每个格子都有𝑎（𝑖,𝑗） = 𝑎(𝑗, 𝑖)，我们就可以直接
将生成的方格𝐷(𝑛, 𝑚)转换成𝐷'（𝑛, 𝑚） [𝑛 ≥ 𝑚]来处理。
于是问题就转化成在𝐷’(𝑛, 𝑚)上寻找一条路径从𝑎(0,0)到达
𝑎(𝑛,𝑚)，使路径上所有的数字之和最小，这样就可以视为一个最
小代价的问题.

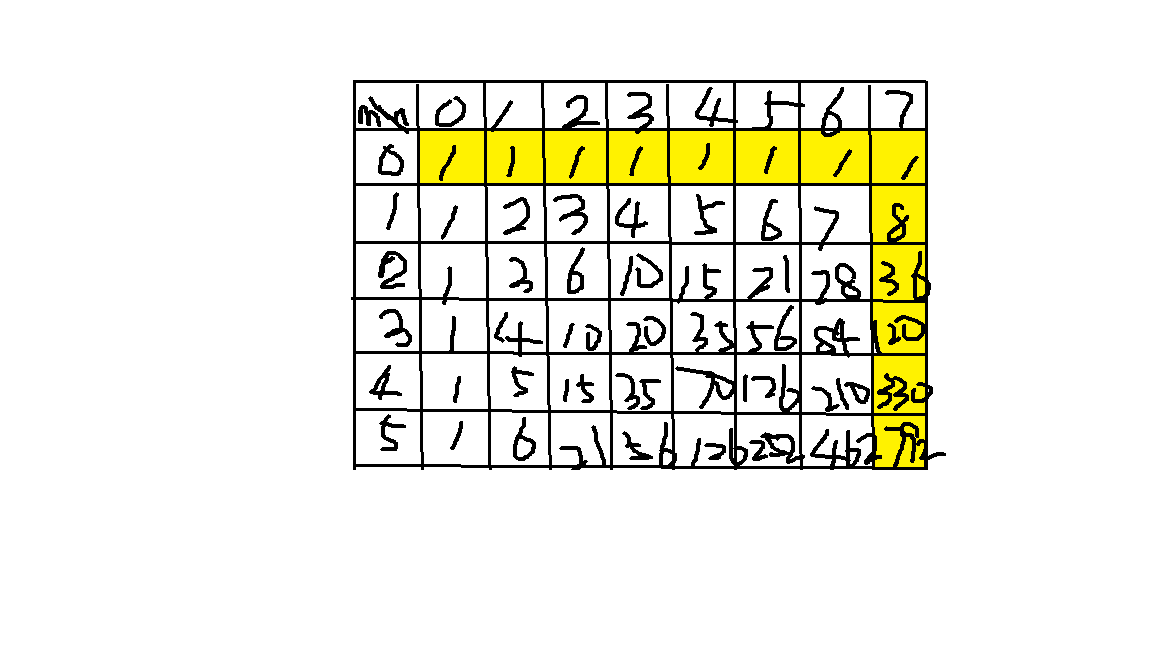
如图的方格𝐷(7,5)，直觉告诉我们图上黄色标注的路径是
代价最小的路径，证明的方法有很多，这里给出一个利用
最短路算法的粗略证明的方法。
首先，我们将每个格子视作一个点，向其相邻的上下左右
四个方向的格子连一条单向边，边权为相邻格子上的数，
此时问题转化为求一条从(0，0）到(𝑛,𝑚）的最短路。思考
SPFA的松弛过程，结合二项式的运算，我们发现，对于任
意的𝐷(𝑛,𝑚)，到达 ( 𝑛,𝑚 )的路径都是由上方边界上的格
子转移过来的，因为每向其他方向转移，所获得的代价都
是位于上方和左边的格子的代价之和，所以对于上边界的
点，向另一个上边界的点转移是最优的，对于向其他方向
的转移的过程，要选择尽量少的点进行转移，所以最短的
路径就是我们标注的路径.
• 最后，最小的和计算就可以表示为:

\[\sum_{i=0}^m \]

• 至此，整个题目就化成了计算:

\[n+C_{n+m+1}^{m} \]