P3800 Power 收集

P3800 Power 收集

这道题花了我一上午加半个下午时间，所以写个博客 “ 庆祝 ” 一下，还是因为我太菜了（蒟蒻）~~~~

---

传送门

总的来说呢，就是给你一个N · M 的矩阵，其中有k个点包含一个带有价值的点，每一行中的一个格子i都可以从上一行中的第 [ i - t , i + t ]个格子中转移过来，求可以获得的最大价值

一眼望去，这不就是dp吗？结果只得了40分，毕竟复杂度为O（$n^3$）,不爆才怪。。好吧，那我们就考虑一下优化吧（就知道蓝题没这么简单）

---

优化

上面我们分析道第 i 行上点的 f[ ] [ ] , 只与第 i - 1 行有关 则可将每相邻的两行 , 单独拆分出来考虑 :

如图：（盗用一下图片）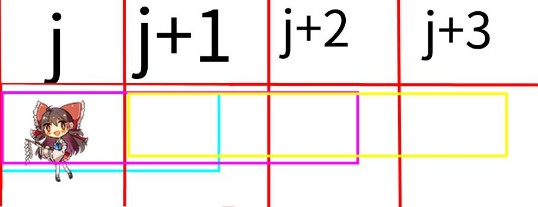 

可以发现 :

1. 转移到 点(i , j)的点 ,为 i - 1行，区间[ j - t，j + t ]中,f[ ][ ]最大的点

2. 转移到 点(i , j + 1 )的点 ,为 i - 1行，区间[ j - t + 1，j + t + 1 ]中,f[ ][ ]最大的点

3. 转移到 点(i , j)的点 ,为 i - 1行，区间[ j - t + 2，j + t + 2 ]中,f[ ][ ]最大的点

后两个区间 , 都可以通过 上一个区间 右移一个单位 得到 这不禁让我们想到了另一道题 : P1886 滑动窗口

obviously，我们可以通过单调队列来进行维护

---

解决

既然每一个格子i都是从上一行第[ i - t ,i + t ]个格子中转移过来，那么我们设a[ i ][ j ]为第 i 行第 j 个点的价值大小，即可轻松得到状态转移方程：

• dp[ i ][ j ]=max(dp[ i - 1 ][ k ])+a[ i ][ j ] ( j - t <= k <= j + t)

• 因此,对于每一个dp[ i ][ j ]来说，他的值均是由上一行中[ j - t , j + t ]区间中的最大值转移过来的

那么obviously，这是一个滑动区间求最值的问题，所以可以考虑用单调队列来优化dp

在进行第ii行第jj列的转移前

利用滑动窗口将第 i - 1 行中[ j - t , j + t ]的最大值来求出来（盗用一下图片）

---

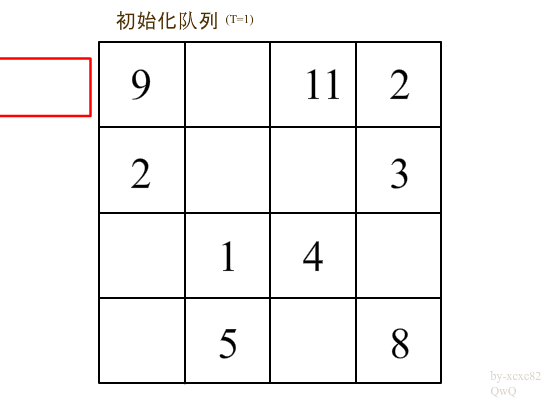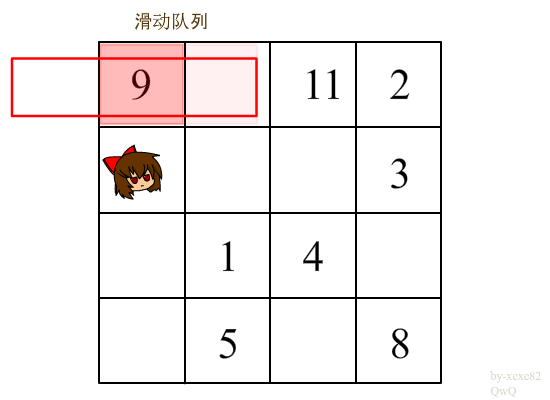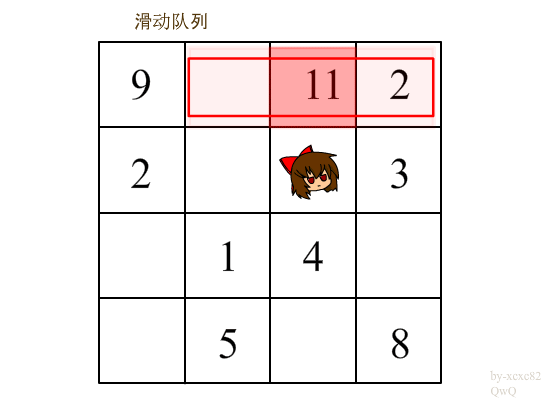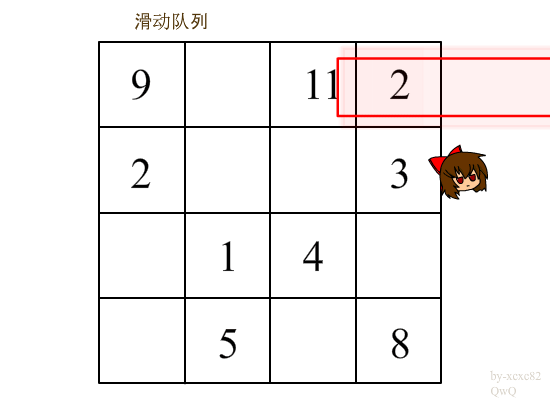
代码分析

首先我们开一个数组 q 来模拟队列,用来滑动求最值

然后初始化第一行dp[ i ][ j ]

第2~n行；利用q求上一行的最大值并进行转移

假设,现在已经更新到第 i 行 :

先初始化单调队列 ,

1. 将能够更新 ( i , 1 ) 的点( i , k ) （ 1 <= k < t + 1 ）,加入单调队列

2. 开始循环 , 更新 [ 1 , M ] 中每一个点 :

• 将能够转移到 j 的最右侧一个点 ( i - 1 , j + t ) , 加入队列

• 使用单调队列找到能够转移到 j 的点的最大f[ ][ ]

• 用最大的f[ ][ ] 更新 f[ i ][ j ]

3. 清空单调队列 , 外层循环进入下一层 ,更新第 i + 1 行

最后找到最后一行中 , 最大的 f[ N ][ j ] , 即所求最值

完结撒花~~~~