[USACO2.4]牛的旅行 Cow Tours

题目描述：这里

思路：

首先，先对整个图进行判连通块，用并查集即可(这一步很重要，因为这可以降低时间复杂度)。

其次，对整个图用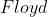求区域内的最短路。

然后，进行暴力，对于不在一个连通块内的两个点，尝试连接它们，求直径的最小值。

注意点：将两个牧场连通后，直径如果要经过新路，可能还比原来牧场的直径小，所以要进行特判。

 

代码部分：

#include<bits/stdc++.h>
using namespace std;

const long double INF = 0x3f3f3f3f3f3f3f3f;

struct dot
{
	int x, y;
}temp[155];

long double len(int x, int y)
{
	return (long double)sqrt((long double)(temp[x].x - temp[y].x) * (long double)(temp[x].x - temp[y].x) + (long double)(temp[x].y - temp[y].y) * (long double)(temp[x].y - temp[y].y));
}

int n;
long double d[155][155];
long double dis[155];

void floyed()
{
    for(int k = 1;k <= n;k++)
        for(int i = 1;i <= n;i++)
            for(int j = 1;j <= n;j++)
                if(d[i][k] != INF && d[k][j] != INF && d[i][j] > d[i][k] + d[k][j])
                    d[i][j] = d[i][k] + d[k][j];
}

int fa[155];

void init()
{
	for(int i = 1;i <= n;i++)
		fa[i] = i;
}

int find(int x)
{
	if(fa[x] == x) return x;
	return fa[x] = find(fa[x]);
}

void merge(int x, int y)
{
	fa[find(x)] = find(y);
}

int main() 
{
	cin >> n;
	init();
	for(int i = 1;i <= n;i++)
		cin >> temp[i].x >> temp[i].y;
	for(int i = 1;i <= n;i++)
		for(int j = 1;j <= n;j++)
		{
			char c;
			cin >> c;
			if(c == '1') 
			{
				d[i][j] = len(i, j);
				merge(i, j);
			}
			else d[i][j] = INF;
		}
	floyed();
	long double ans = 0x3f3f3f3f3f3f3f3f, sum = 0, maxa = INT_MIN, maxb = INT_MIN;
	int mina, minb;
	for(int i = 1;i <= n;i++)
		for(int j = i + 1;j <= n;j++)
			if(find(i) != find(j))
			{
				sum += len(i, j);
				mina = i;
				minb = j; 
				for(int k = 1;k <= n;k++)
					if(find(mina) == find(k) && k != mina)
					{
						if(d[mina][k] != INF) maxa = max(maxa, d[mina][k]);
						if(d[k][mina] != INF) maxa = max(maxa, d[k][mina]);
					}
				if(maxa >= 0) sum += maxa;
				for(int k = 1;k <= n;k++)
					if(find(minb) == find(k) && k != minb)
					{
						if(d[minb][k] != INF) maxb = max(maxb, d[minb][k]);
						if(d[k][minb] != INF) maxb = max(maxb, d[k][minb]);
					}
				if(maxb >= 0) sum += maxb;
				ans = min(ans, sum);
				sum = 0;
				maxa = INT_MIN, maxb = INT_MIN;
			}
	for(int i = 1;i <= n;i++)
		for(int j = 1;j <= n;j++)
			if(d[i][j] != INF) 
				dis[i] = max(dis[i], d[i][j]);
	for(int i = 1;i <= n;i++)
		ans = max(ans, dis[i]);
	cout << fixed << setprecision(6) << ans << endl;
	return 0;
}