埃拉托斯特尼筛法的应用--求素数，亲和数

写一个程序求某一给定范围的素数（质数），我想这个问题对于大部分人来说都是很easy的事情。似乎在刚开始学程序设计的时候，谭浩强老师的那本C语言课本里就有相应的解法。以前的我只知道怎么去求解这个问题，但对于这个方法的来源不是很清楚。今天忽然间从一个题目（接下来要讲的亲和数问题）里得到了这个方法的名称，原来这是有名的埃拉托斯特尼筛法。 先对着维基百科讲解一下这个方法求解素数的基本原理：

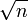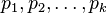给出要筛数值的范围n，找出以内的素数。先用2去筛，即把2留下，把2的倍数剔除掉；再用下一个质数，也就是3筛，把3留下，把3的倍数剔除掉；接下去用下一个质数5筛，把5留下，把5的倍数剔除掉；不断重复下去......。

步骤

详细列出算法如下：

1. 列出2以后的所有序列：
   • 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25
2. 标出序列中的第一个素数，也就是2，序列变成：
   • 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25
3. 将剩下序列中，划摽2的倍数（用红色标出），序列变成：
   • 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25
4. 如果现在这个序列中最大数小于最后一个标出的素数的平方，那么剩下的序列中所有的数都是素数，否则回到第二步。

---

1. 本例中，因为25大于2的平方，我们返回第二步：
2. 剩下的序列中第一个素数是3，将主序列中3的倍数划出（红色），主序列变成：
   • 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25

1. 我们得到的素数有：2，3
2. 25仍然大于3的平方，所以我们还要返回第二步：
3. 现在序列中第一个素数是5，同样将序列中5的倍数划出，主序列成了：
   • 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25
4. 我们得到的素数有：2 3 5 。
5. 因为25等于5的平方，跳出循环.

结论：去掉红色的数字，2到25之间的素数是：2 3 5 7 11 13 17 19 23。

贴出我的代码求出1-N范围内的素数。

#include <stdio.h>
#include <math.h>
#include <stdlib.h>

#define BITSPERWORD 32
#define SHIFT 5
#define MASK 0x1F
#define N 1000000

int bitsArr[N/BITSPERWORD];  //选择使用了bitmap方法

void set(i){bitsArr[i >> SHIFT] |= (1 << (i & MASK));}
int test(i){return bitsArr[i >> SHIFT] & (1 << (i & MASK));}
int main(){
	int i,j;
	for(i = 2;i <= sqrt(N);i++){
		if(test(i)) continue;	
		j = i*i;//注意这个技巧
		while(j <= N){
			set(j);
			j += i;
		}
	}

	for(i = 2;i <= N;i++){
		if(!test(i)) printf("%3d ",i);	
	}
}

由于代码的意图简单，所有就不用具体讲解了。

接下来我来详述一下今天遇到的一个问题：

题目描述： 求500万以内的所有亲和数

亲和数定义：如果两个数a和b，a的所有真因数之和等于b，b的所有真因数之和等于a，则称a,b是一对亲和数。

刚开始分析这个问题的时候我觉得解决这个问题需要分为两大步骤，首先求出1 - 500 0000 之间的没一个数字的所有真因数，然后用数组存放每一个数（数组下标）的真因子之和。接着第二大任务就是好遍历该结果数组，查找相同元素。对于第二个任务，对数组的映射能力理解良好的人都能够想得出这个靠谱的办法，用下标表示数字，用下标中存储的值代表真因子之和，这样我们只需要给一个这样的判断就可以了，即arr[arr[i]]==i；是不是？然而我在对每一个数求真因子的这个问题一直比较纠结，先求真因子集合，再求集合的和。是不是问题搞复杂了。我实在想不出好的办法了，就求助于网络上的解答，结果发现似乎原理和求素数的埃拉托斯特尼筛法雷同。大概的思路是这样的，分配一个500 0001大小的数组，然后每一个置为1，为啥呢？因为每一个数的真因数集合中肯定包括1，将每一个包含该真因数的数加上这个因子，然后再接着递增这个真因数，真因数最大为多少呢？要求的那个数的一半嘛！（不用解释） 当结束的时候，数组里存放的就是每一个数（数组下标）的真因子之和。接下来的任务就是遍历了，很简单！ 可能叙述的不大清楚，直接看代码也许更容易理解一点，个人文字表达能力不是很好，请体谅，呵呵！

#include <stdio.h>
#include <stdlib.h>
#define N 5000000
int arr[N+10];
int main(){
	int i,j;
	for(i = 1;i <= N;i++) arr[i] = 1;
	for(i = 2;i + i <= N;i++){
		j = i + i;//注意真因子不包括本身
		while(j <= N){
			arr[j] += i;
			j += i;
		}
	}

	for(i = 2;i <= N;i++){
		if((arr[i] > i)&&(arr[i]<=N)&&(arr[arr[i]] == i)) printf("%5d   %5d\n",i,arr[i]);//注意第二个条件必须放在第三个之前，防止出现内存访问错误
	}
}

参考：

1 http://zh.wikipedia.org/zh-cn/%E5%9F%83%E6%8B%89%E6%89%98%E6%96%AF%E7%89%B9%E5%B0%BC%E7%AD%9B%E6%B3%95

2 http://blog.csdn.net/v_JULY_v