洛谷P1115 最大子段和

洛谷链接
acwing题解

法1

动态规划
分析：如果前面的子段加上第i个数是变大的就加上，如果变小则单独成为一个序列
状态表示：f[i]表示到i个数字位置的最大子段和的最大值
状态计算：f[i]分为包含第i个数的子段 和 自己重新开一个子段**
状态转移方程： f[i] = max(f[i - 1] + a[i], a[i])
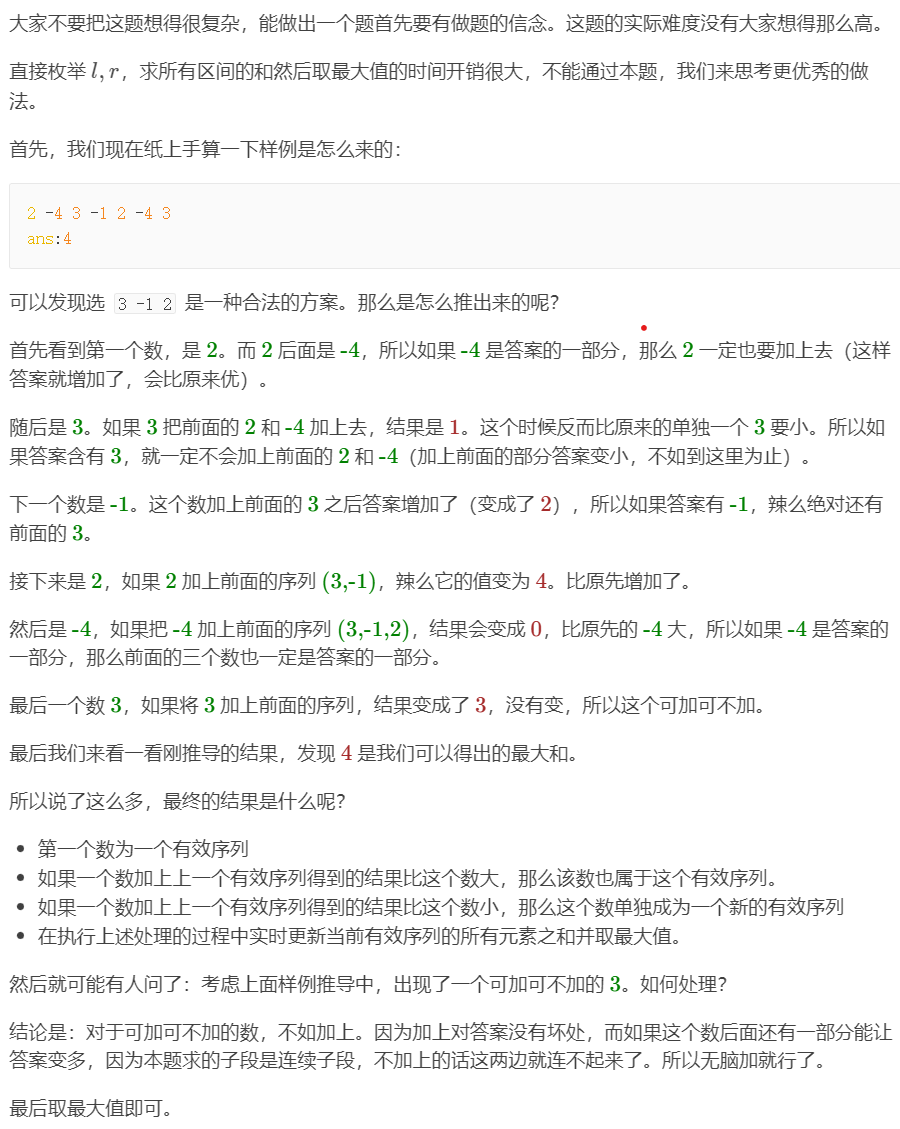
贪心思想：对于可加可不加的数，不如加上。因为加上对答案没有坏处，而如果这个数后面还有一部分能让答案变多，因为本题求的子段是连续子段，不加上的话这两边就连不起来了。所以无脑加就行了。

• 第一个数为一个有效序列
• 如果一个数加上上一个有效序列得到的结果比这个数大，那么该数也属于这个有效序列。
• 如果一个数加上上一个有效序列得到的结果比这个数小，那么这个数单独成为一个新的有效序列
• 在执行上述处理的过程中实时更新当前有效序列的所有元素之和并取最大值。
  

#include <iostream>
#include <cstring>
#include <algorithm>

using namespace std;

const int N = 2e5 + 10;

int n;
int f[N];
int a;
int ans = -1e9;  //注意a的范围是-1e4，所以定义ans为比它小的，否则会出错

int main ()
{
    cin >> n;
    
    for(int i = 1; i <= n; i ++)
    {
        cin >> a;
        f[i] = max(f[i - 1] + a, a);
        ans = max(f[i], ans);
    }
    
    cout << ans << endl;
    
    return 0;
}

法2

用s 来存 以前一个数为结尾子数组的和最大是多少

枚举输入的x

1. s > 0 ：s += x, s大于0则接上一定比不接更大
2. s < 0 : s = x， s小于0则不接上一定比接上更大
3. s = 0 ：s为0，加不加都可以
   3和2两类可以和为1类， s <= 0 , s = x;

#include <iostream>
#include <cstring>
#include <algorithm>

using namespace std;

int n;
int a;
int ans = -1e9;
int s;

int main ()
{
    cin >> n;
    
    for(int i = 1; i <= n; i ++)
    {
        cin >> a;
        if(s < 0) s = 0;
        s += a;
        
        //等价于
        // if(s >= 0) s += a;
        // else s = a;
        ans = max(ans, s);
    }
    
    cout << ans << endl;
    
    return 0;
}