[蓝桥杯 2013 省 A] 剪格子

[蓝桥杯 2013 省 A] 剪格子

[蓝桥杯 2013 省 A] 剪格子

题目描述

如图 $1$ 所示，$3\times 3$ 的格子中填写了一些整数。

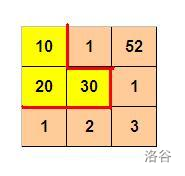
我们沿着图中的红色线剪开，得到两个部分，每个部分的数字和都是 $60$。

本题的要求就是请你编程判定：对给定的 $m\times n$ 的格子中的整数，是否可以分割为两个部分，使得这两个区域的数字和相等。

如果存在多种解答，请输出包含左上角格子的那个区域包含的格子的最小数目。

如果无法分割，则输出 $0$。

输入格式

程序先读入两个整数 $m$，$n$ 用空格分割 $(m,n<10)$
表示表格的宽度和高度。

接下来是 $n$ 行，每行 $m$ 个正整数，用空格分开。每个整数不大于 $10000$。

输出格式

程序输出：在所有解中，包含左上角的分割区可能包含的最小的格子数目。

样例 #1

样例输入 #1

3 3
10 1 52
20 30 1
1 2 3

样例输出 #1

3

样例 #2

样例输入 #2

4 3
1 1 1 1
1 30 80 2
1 1 1 100

样例输出 #2

10

提示

第二个用例中：

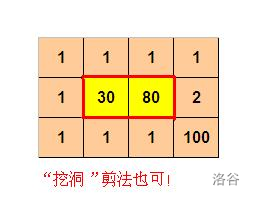
时限 5 秒, 64M。蓝桥杯 2013 年第四届省赛

#include <iostream>

using namespace std;

const int N = 11;

int n, m;
int w[N][N];
int dx[4] = {-1, 0, 1, 0}, dy[4] = {0, 1, 0, -1};
int cnt = 1;
bool st[N][N];
int t;
int res = 1e9;

void dfs(int x, int y, int sum)
{
    if(sum == t - sum)
    {
        res = min(res, cnt);
        return ;
    }
    // cout << sum << endl;
    st[x][y] = true;
    
    for(int i = 0; i < 4; i ++)
    {
        int a = x + dx[i], b = y + dy[i];
        
        if(a < 0 || b < 0 || a >= n || b >= m) continue;
        if(st[a][b]) continue;
        if(sum + w[a][b] > t - sum) continue;
        st[a][b] = true;
        cnt ++;
        dfs(a, b, sum + w[a][b]);
        st[a][b] = false;
        cnt --;
    }
}

int main ()
{
    cin >> m >> n;
    for(int i = 0; i < n; i ++)
        for(int j = 0; j < m; j ++)
        {
            cin >> w[i][j];
            t += w[i][j];
        }
    dfs(0, 0, w[0][0]);
    
    cout << res;
    
    return 0;
}

心得体会：

1. 读入顺序为m， n
2. dfs遍历