视觉测量中的变换关系

1.平移变换（Translation）

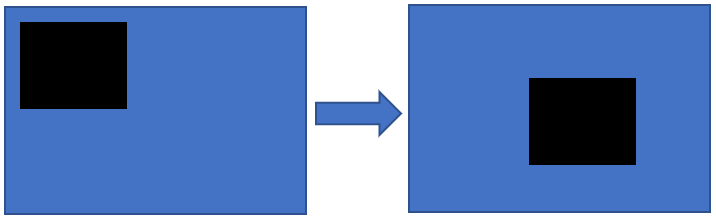
\[\left\{ \begin{array}{l}
{\rm{x'}} = x + {t_x}\\
y' = y + {t_y}
\end{array} \right.\]

写成矩阵为:

\[\left[ {\begin{array}{*{20}{c}}
{{\rm{x}}'}\\
{y'}
\end{array}} \right] = \left[ {\begin{array}{*{20}{c}}
1&0&{{t_x}}\\
0&1&{{t_y}}
\end{array}} \right]\left[ {\begin{array}{*{20}{c}}
x\\
y\\
1
\end{array}} \right]\]

齐次坐标形式为:

\[\left[ {\begin{array}{*{20}{c}}
{{\rm{x}}'}\\
\begin{array}{l}
y'\\
1
\end{array}
\end{array}} \right] = \left[ {\begin{array}{*{20}{c}}
1&0&{{t_x}}\\
\begin{array}{l}
0\\
0
\end{array}&\begin{array}{l}
1\\
0
\end{array}&\begin{array}{l}
{{\rm{t}}_y}\\
1
\end{array}
\end{array}} \right]\left[ {\begin{array}{*{20}{c}}
x\\
y\\
1
\end{array}} \right]\]变量为2个自由度。

2.旋转变换（Euclidean变换）

 

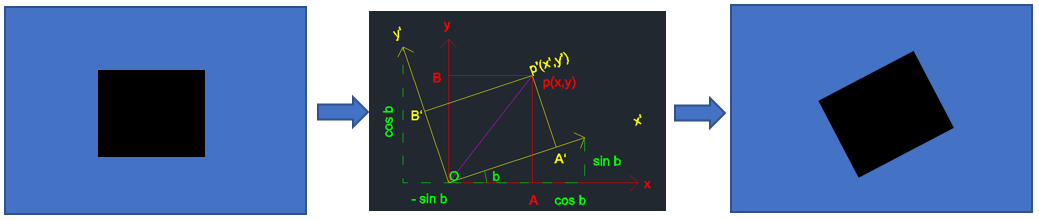
用单位向量表示为：

\[\left\{ \begin{array}{l}
\overrightarrow {\rm{x}} {\rm{' = }}\overrightarrow {\rm{x}} \cos b + \overrightarrow y \sin b\\
\overrightarrow y ' = - \overrightarrow x \sin b + \overrightarrow y \cos b
\end{array} \right.\]

P在坐标系中关系表示为:

$$\left[ {\begin{array}{*{20}{c}}
{{\rm{OA}}}\\
{OB}
\end{array}} \right] = \left[ {\begin{array}{*{20}{c}}
{\cos b}&{ - \sin b}\\
{\sin b}&{\cos b}
\end{array}} \right]\left[ {\begin{array}{*{20}{c}}
{{\rm{OA'}}}\\
{{\rm{OB'}}}
\end{array}} \right]$$

将xy坐标系和x’y’坐标系建立起了联系。加入上面的平移变换写成齐次形式为：

\[\left[ {\begin{array}{*{20}{c}}
{{\rm{x}}'}\\
\begin{array}{l}
y'\\
1
\end{array}
\end{array}} \right] = \left[ {\begin{array}{*{20}{c}}
{\cos \theta }&{{\rm{ - }}\sin \theta }&{{t_x}}\\
\begin{array}{l}
\sin \theta \\
0
\end{array}&\begin{array}{l}
\cos \theta \\
0
\end{array}&\begin{array}{l}
{{\rm{t}}_y}\\
1
\end{array}
\end{array}} \right]\left[ {\begin{array}{*{20}{c}}
x\\
y\\
1
\end{array}} \right]\]平移2个自由度加旋转一个自由度总共3个自由度。

3.相似变换（Similarity transform）

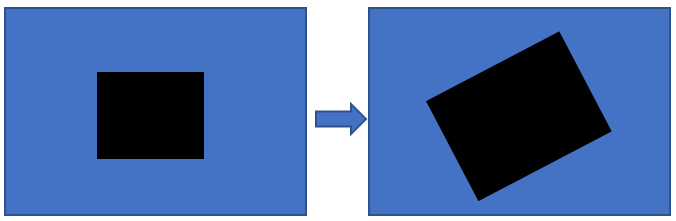
\[\left[ {\begin{array}{*{20}{c}}
{{\rm{x}}'}\\
\begin{array}{l}
y'\\
1
\end{array}
\end{array}} \right] = \left[ {\begin{array}{*{20}{c}}
{\alpha \cos \theta }&{{\rm{ - }}\alpha \sin \theta }&{{t_x}}\\
\begin{array}{l}
\alpha \sin \theta \\
0
\end{array}&\begin{array}{l}
\alpha \cos \theta \\
0
\end{array}&\begin{array}{l}
{{\rm{t}}_y}\\
1
\end{array}
\end{array}} \right]\left[ {\begin{array}{*{20}{c}}
x\\
y\\
1
\end{array}} \right]\]基于以上的变换又多了一个比例系数为4个自由度。

4.仿射变换（Affine transform）

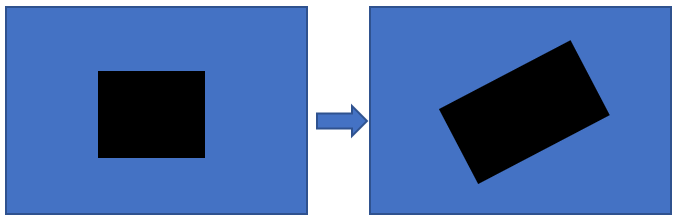
\[\left[ {\begin{array}{*{20}{c}}
{{\rm{x}}'}\\
\begin{array}{l}
y'\\
1
\end{array}
\end{array}} \right] = \left[ {\begin{array}{*{20}{c}}
{\rm{a}}&b&c\\
\begin{array}{l}
d\\
0
\end{array}&\begin{array}{l}
e\\
0
\end{array}&\begin{array}{l}
f\\
1
\end{array}
\end{array}} \right]\left[ {\begin{array}{*{20}{c}}
x\\
y\\
1
\end{array}} \right]\]

为6个自由度.

5.透视变换

 

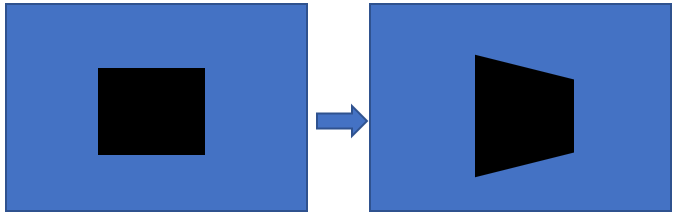
我们人眼通过窗外看外面的景物，景物投射到玻璃上面的现状就是最典型的例子。我们看的角度不同，在玻璃上投射的情况就不同。物体的基本形状已经改变。

\[\left[ {\begin{array}{*{20}{c}}
{{\rm{x}}'}\\
\begin{array}{l}
y'\\
w'
\end{array}
\end{array}} \right] = \left[ {\begin{array}{*{20}{c}}
{\rm{a}}&b&c\\
\begin{array}{l}
d\\
{\rm{g}}
\end{array}&\begin{array}{l}
e\\
h
\end{array}&\begin{array}{l}
f\\
1
\end{array}
\end{array}} \right]\left[ {\begin{array}{*{20}{c}}
x\\
y\\
1
\end{array}} \right]\]为8个自由度。