经典backbone——ResNet

ResNet——Residual Network

Deep Residual Learning for Image Recognition

Identity Mappings in Deep Residual Networks

Wide Residual Network

最原始的ResNet

卷积神经网络(Convolutional Neural Network)正不断朝着“Deep”这个方向发展，最早期的LeNet只有5层，后来VGG把深度增加到19层，而我们即将要介绍的ResNet，更是超过了100层。

于是我们的 only true god-何恺明提出一个问题：

Is learning better networks as easy as stacking more layers？

答案是否定的，单纯地增加网络层数，提高深度，不仅不会得到更好的效果，反而会使误差增大！

img

img

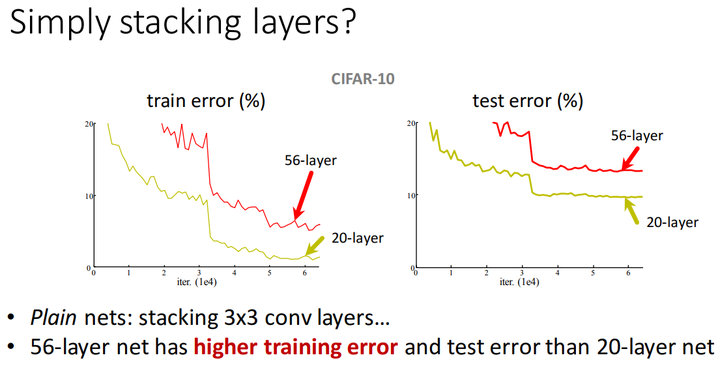
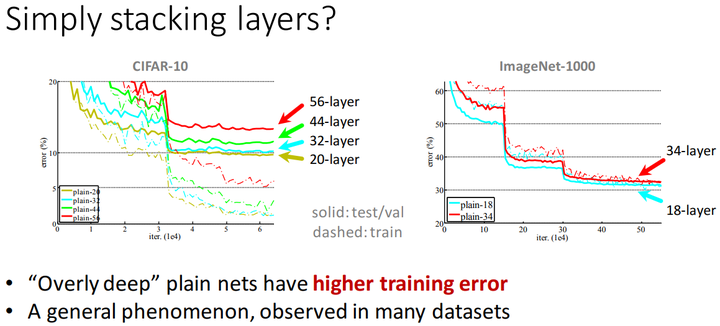
多个datasets的测试表明，仅仅只是简单地堆叠卷积层，并不能让网络训练得更好。

img

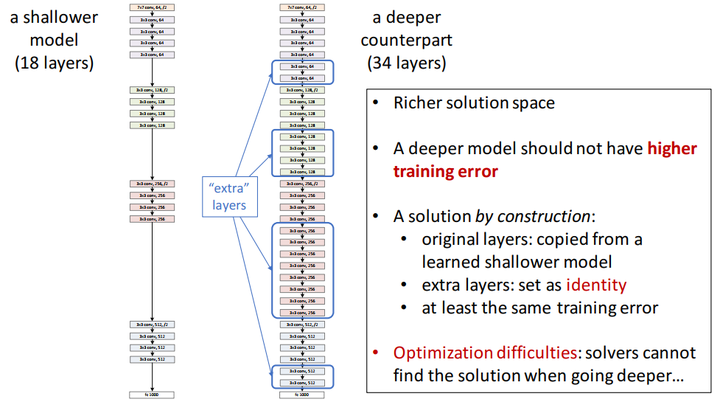
按理来说，如果网络加深，training acc应该增大，而testing acc减小，但是上图并不是这么回事，于是乎，Kaiming He提出了Deep Residual Learning的架构。

关于残差模块(residual block)

恺明老师首先引入了一个残差模块(residual block)的概念

img

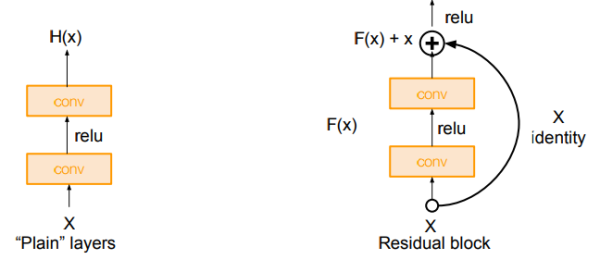
输入为\(x\)，需要拟合的结果为\(H(x)\)，此时我们将输出差分为\(x+y\)，也就是\(H(x)=x+y\)。

再令\(y=F(x)\)，即通过正常的卷积产生的结果，最后两者相加即为残差块输出。

img

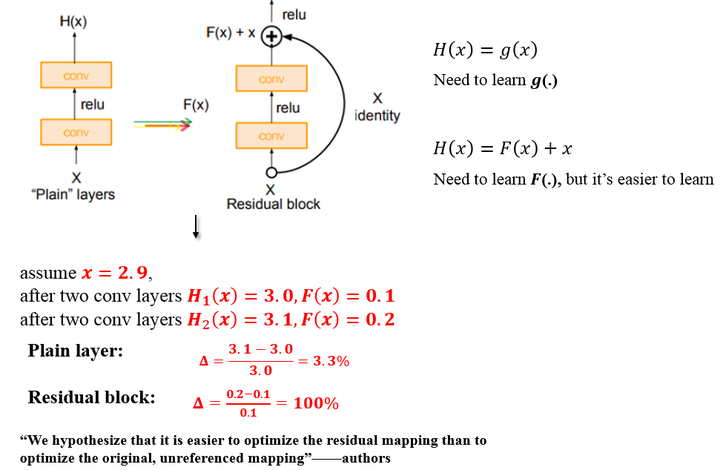
因为\(x\)本身就是输出，所以我们只需要拟合\(F(x)\)即可

如上图，原始的plain架构，我们用两层卷积层来模拟函数\(g(\cdot)\)，而在residual block中，我们用两层卷积层来模拟函数\(F(\cdot)\)

举个例子：

输入\(x=2.9\)，经过拟合后的输出为\(H(x)=3.0\)，那么残差就是\(F(x)=H(x)-x=0.1\)。如果我们拟合的是恒等变换，即输入\(x=2.5\)，输出还是\(H(x)=2.5\)，那么残差就是\(F(x)=H(x)-x=0.0\)

如上图所示，假设\(x\)从\(2.9\)经过两层卷积层(cov)后变为\(3.1\)，普通网络的变化率为\(\bigtriangleup =\frac{3.1-3.0}{3.0}=3.3%\)，而残差模块的变化率为\(\bigtriangleup =\frac{0.2-0.1}{0.1}=100%\)

残差的引入去掉了主体部分，从而突出了微小的变化

网络结构

有了残差模块(residual block)这个概念，我们再来设计网络架构，
架构很简单，基于VGG19的架构，我们首先把网络增加到34层，增加过后的网络我们叫做plain network，再此基础上，增加残差模块，得到我们的Residual Network

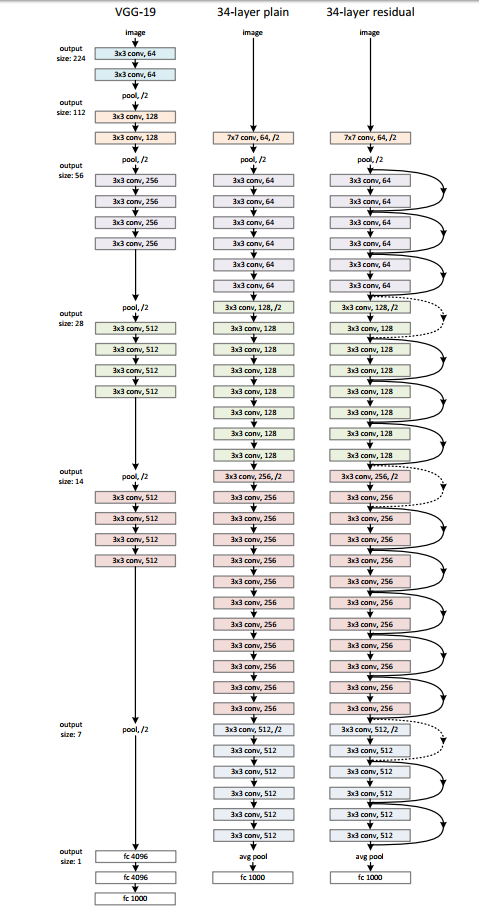
preview

img

虚线部分，维度增加，亦即卷积核(filters)数目增加的过程，这个时候\(F(x)+x\)就会出现维度不匹配现象，所以就出现后面用\(1\times 1\)的conv来提高维度,然后再进行相加的操作.

关于bottle neck

论文中有两种residual block的设计，如下图所示：

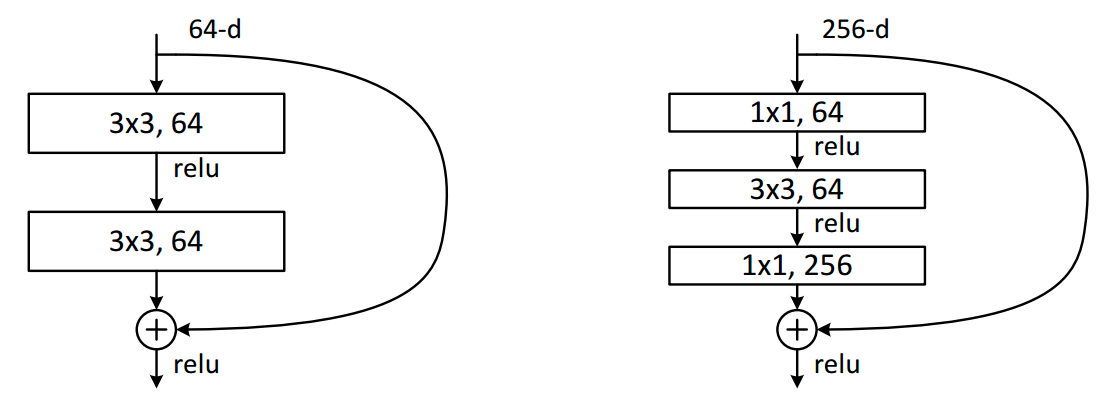
preview

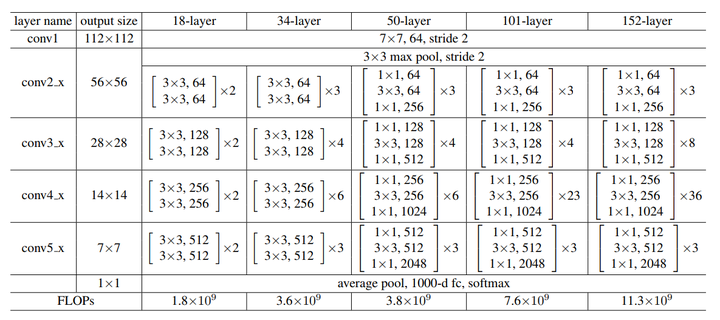
在训练浅层网络的时候，我们选用前面这种，而如果网络较深(大于50层)时，会考虑使用后面这种(bottle neck)，这两个设计具有相似的时间复杂度。

conv虽然写的是\(3\times 3\)，但实际上应该是\(64（上一层channel数）\times 3\times 3（conv filter的大小）\times 64（输出的channel数目）\)

同样举个例子：
对于ImageNet而言，进入到第一个residual block的input为\((56,56,64)\)，采用左侧的两个\(3\times 3\)conv的卷积层：参数量为\((3\times 3\times 64)\times 64+(3\times 3\times 64)\times 64\)，化简一下：\(params:(18\times 64)\times 64=73728\)
采用右侧的的bottle neck：参数量为\((1\times1\times64)\times 256+(3\times3\times 64)\times64+(1\times1\times 256)\times 64\) ，化简一下：\(params:(10\times 64)+2\times 64 \times256=53248\)

可以看到它们的参数量属于同一个量级，
但是这里bottleneck占用了整个network的「三层」，而原本只有「两层」，
所以这样就节省了大量的参数，
在大于50层的ResNet中，他们使用了bottle neck这种形式。

具体细节如图所示：

img

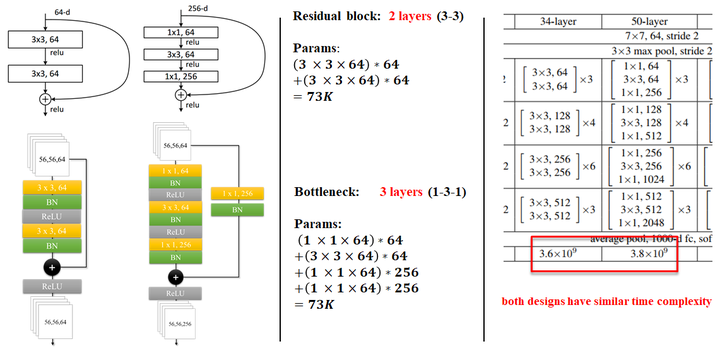
ResNet 改进 Identity mapping(恒等变换)

我们来仔细分析一下Residual Block, 在这篇paper中也被叫为Residual Unit.

对于原始的 Residual Unit(block),我们有如下计算：

\[\begin{matrix}y_l=h(x_l)+\mathcal{F}(x_l,\mathcal{W}_l)\\x_{l+1}=f(y_l)\end{matrix} \]

\(x_l\)表示第\(l\)个Residual Unit的输入， \(y_l\)则代表第\(l\)个Residual Unit的输出，\(h\)代表的某个变换，在此处是恒等变换，\(\mathcal{F}\)代表residual function，\(f\)代表某种操作，在这里是ReLU 。

所以可以写成如下形式：

\[\begin{matrix}y_l=x_l+\mathcal{F}(x_l,\mathcal{W}_l)\\x_{l+1}=ReLU(y_l)\end{matrix} \]

img

也就是Residual Unit一开始的做法了。

那如果，我们\(f\)是恒等变换呢，即\(x_l+1\equiv y_l\)，那么有：

\[x_{l+1}=y_l=x_l+\mathcal{F}(x_l,\mathcal{W}_l) \]

对于任意一层，我们都能用这个公式来表示：

\[X_L=x_l+\sum^{L-1}_{i=l}\mathcal{F}(x_i,\mathcal{W}_i) \]

img

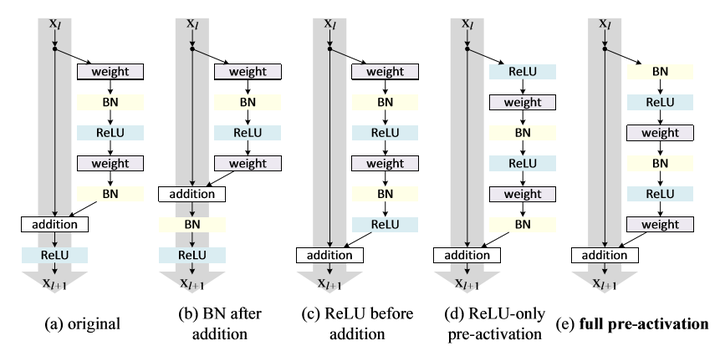
这便是这篇paper的改进，把原本的ReLU，放到Residual Unit的conv前面去，而不是放在addition之后。

img

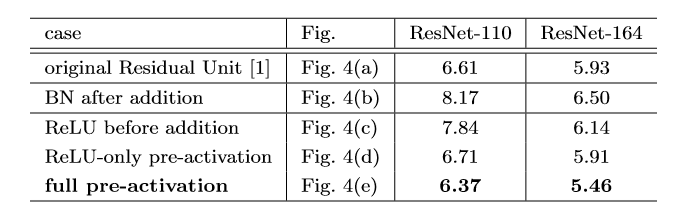
可以看到，在上图作者对cifar10进行的多组实验中，使用full pre-activation这种Residul Unit效果最佳，个人认为这张表格还是挺重要的，我们简单分析一下！

  • (a)original：原始的结构
  • (b)BN after addition：这是在做相反的实验，本来我们的目的是把ReLU移到旁路上去，这里反而把BN拿出来，这进一步破坏了主路线上的恒等关系，阻碍了信号的传递，从结果也很容易看出，这种做法不ok
  • (c)ReLU before addition：将\(f\)变为恒等变换，最容易想到的方法就是将ReLU直接移动到BN后面，但这会出现一个问题，一个\(\mathcal{F}\)(残差函数)的输出应该可以是\((-\infty,\infty)\) ,但是经过ReLU之后就会变为\((0,\infty)\)​，这种做法的结果也比(a)要差。

直接提上来似乎不行，但是问题反过来想， 在addition之后做ReLU，不是相当于在下一次conv之前做ReLU吗？

  • (d)ReLU-only pre-activation：根据刚才的想法，我们把ReLU放到前面去，然而我们得到的结果和(a)差不多，原因是什么呢？因为这个ReLU层不与BN层连接使用，因此无法共享BN所带来的好处。
  • (e)full pre-activation：啊，那要不我们也把BN弄前面去，惊喜出现了，我们得到了相当可观的结果，是的，这便是我们最后要使用的Unit结构！！！

Wide Residual Network

img

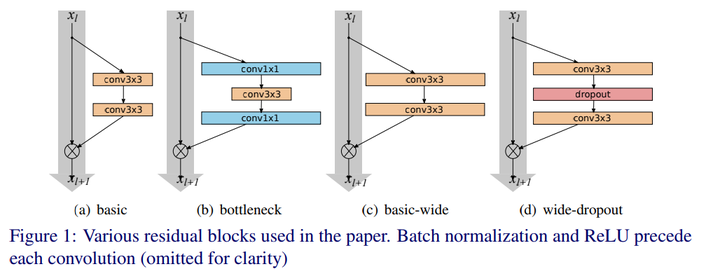
原始的ResNet如(a)和(b)所示，(b)是使用了bottleneck的residual block，而(c)和(d)便是WRN这篇paper的作者提出的架构。他认为一味的增加深度并不是最有效的方法，residual block的宽度对网络性能的提升更有帮助。所以他考虑增加每一层的宽度(身材修长固然好，但是太瘦便是营养不良，稍微长结实点，也许会更好，貌似家长是这个观点)。

About block type

  1. \(B(3,3)\)- original <<basic>> block
  2. \(B(3,1,1)\)- with one extra \(1\times 1\) layer
  3. \(B(1,3,1)\)- with the same dimensionality of all convolutions,<<straightened>> bottle neck
  4. \(B(1,3)\)- the network has alternating \(1\times 1\sim 1\times 3\) convolutions everywhere
  5. \(B(3,1)\)- similar idea to the previous block
  6. \(B(3,1,1)\)- Network-in-Network style block

\(B(3,3)\)和\(B(1,3,1)\)是原始paper中有实验的block，\(B(3,1,1)\)类似于NIN的block。
对以上这些residual block，作者使用了\(k=2\)来进行测试，结果表明\(B(3,3)\)最好。

img

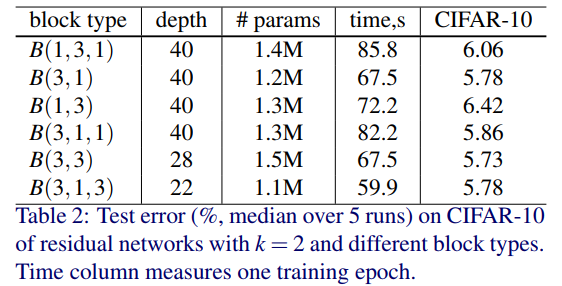
所以作者后来实验的baseline使用的是resnet最原始的两个conv3x3的residual block，上图中右侧的\(k\)，就是增加宽度的倍数，如果\(k=1\) ，就是原本的ResNet。

img

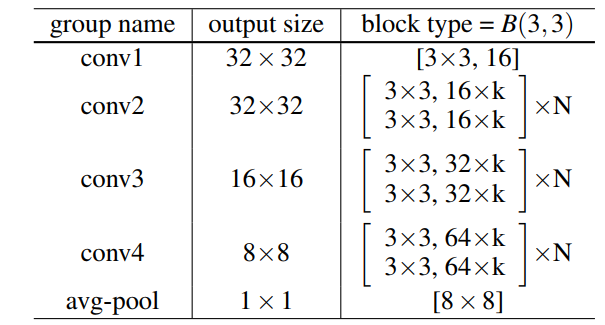
Experimental results

从实验的结果来看，也是一目了然，WRN的40-4架构就可以和ResNet的1001层相比，当然，训练时间的话还是WRN更少。
另外可以看出，深度和宽度都会为网络的性能提高带来好处。

img

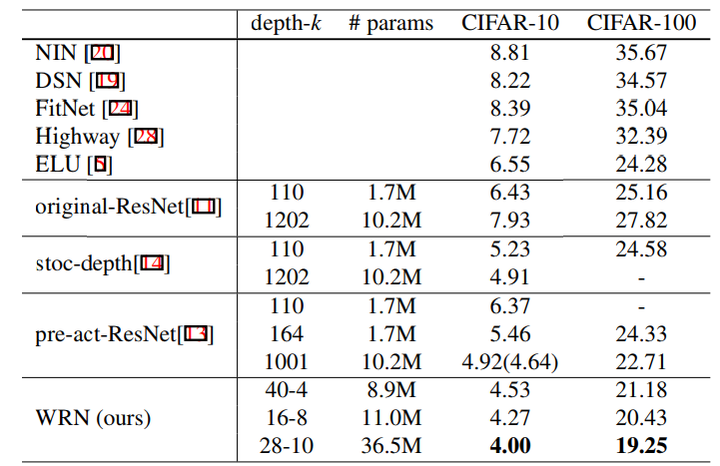
About Dropout

网络深度和宽度的加深，会增加训练的参数量，导致过拟合，作者提出的另一个idea便是在residual block里面加入dropout，也是就开头讲到的(d)

img

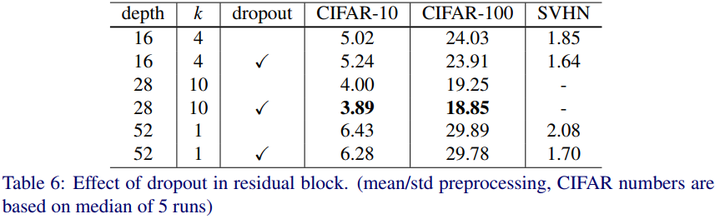
从实验结果看，也能说明，当网络层\(depth\)数较浅，或者宽度\(k\)较小时，网络还不需要加dropout，但是当层数增加，宽度增加，参数量指数增大时，加入dropout可以有效防止model的overfitting。

ResNeXt

很多人认为ResNeXt没什么创新点，原因如下：

  1. 结构照搬Inception
  2. 实现只加了个分组卷积，变化微乎其微

因此乏善可陈。但这反而是ResNeXt的闪光点，只是这闪光点略有些眩目而已。因为若仔细想想，“照搬Inception”必然导致模型复杂，而实现起来却又“变化微乎其微”，这两者之间有巨大的矛盾。

但随着阅读论文/梳理思路/实现模型，再根据模型重新阅读论文梳理思路，进而修改实现这么循环下来，“吃透了”ResNeXt，才发现它的趣味所在。

通过“同构”的简洁，四两拨千斤地击败复杂的Inception，还含蓄地动摇了Inception的出发点。

Abstract

  • 借鉴Inception的“分割-变换-聚合”策略，却用相同的拓扑结构组建ResNeXt模块。
  • 简洁：同构多分枝，因此有更少的超参数
  • 引入“基数”（cardinality），基数增加可提高模型效果。比变深or变宽还好使。

Introduction

现在的研究方向已经从早年寻找各类手工设计特征（如SIFT和HOG）的“特征工程”（feature engineering）到寻找高效网络结构的“网络工程”（network engineering）发展。但由于大家设计网络的骚操作五花八门，搞得超参数越来越多，所以现在设计结构也变得越来越难了……

VGG则是个清流，它采用了非常简练的设计原则：堆叠相同形状的模块（blocks）。这种思考方法ResNet用了都说好，只不过ResNet采用相同形状的“残差块”（Residual Blocks）。

这样做不仅满足了广大处女座强迫症患者，最大的好处在于网络结构有关的超参数只涉及深度和宽度，那么调参就不用那么疯狂了。

要知道如果超参数太多，调起来麻烦不说，有时候自己都不知道到底哪个参数解决了问题，碰到新问题可能原来调好的模型就又歇逼了。（存在一组过于精细的超参数只对特定数据集有效的风险）。

而VGG同期反其道而行之的Inception，则使用了一套精心设计的网络结构，通过卷积层之间的稀疏连接达到了很好的效果。Inception将输入通过\(1*1\)conv分到几个低维嵌入。然后用一套特殊的卷积核处理，最后接在一起合成。这就是它特有的“分割-变换-融合”策略。

注：稀疏表示指每个block中有几个不同的分支，相互独立互不影响，只在最后把他们的输出拼接在一起（concatenation）。

这么做的好处是，这个Block所能表示的解空间，实际上是一个更大卷积核的严格子空间。但本身复杂度很小。

说人话：Inception用了小卷积核的计算量干了大卷积核的事情，效果还差不多。

Inception的作者认为，Inception的优势更多在于通过精心设计的复杂Block结合多个感受野的特征。但这就正中了一开始分析的下怀：针对问题尽心设计的精巧结构往往会失去足够的泛化性。

那么问题来了，Inception的能力之所以优越，究竟是因为它引以为傲的复杂结构，还是别的什么？

比如，“分割-变换-融合”策略（稀疏连接）？

从“分割-变换-融合”到聚合变换

“分割-变换-融合”这技术看起来唬人，但实际上却也一直在我们身边。

1.重新思考神经元

img

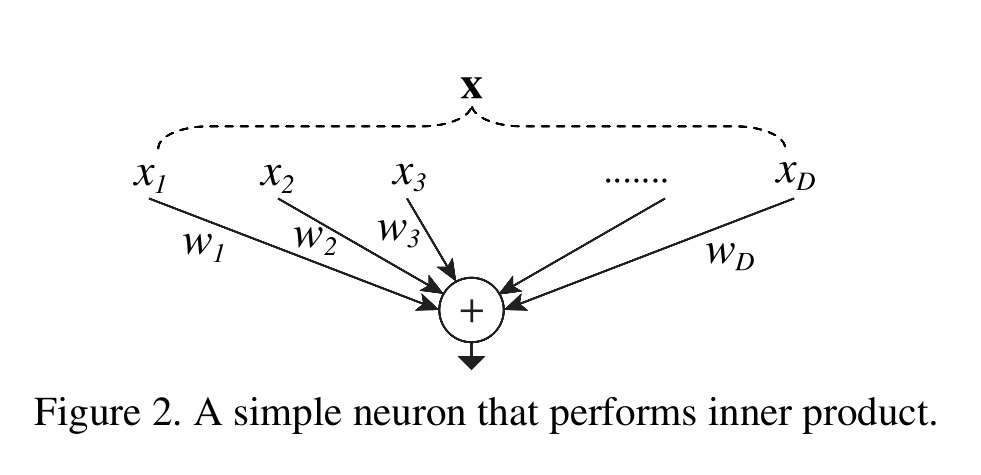
很久很久以前，在CNN还没有大行其道，人们还管全连接层叫神经网络的时候。最常见也是最简单的运算就是输入向量与权重的内积了，而这本来就是一种聚合变换。

\[\underset{i=1}{\overset{D}{\sum}}w_ix_i \]

其中\(X=[x_1,x_2,...,x_D]\)是D通道的输入向量，\(w_i\)则是对应\(i\)通道的权重。现在我们用之前“分割，变换，聚合”的角度重新描述一下内积过程：

  1. 分割：向量\(X\)被分成了D个低维嵌入，内积中则被直接分成了一个个1维子空间\(x_i\)
  2. 变换：模型对低维表示进行变换，这里只是简单的乘了一个数，变成了\(w_ix_i\)
  3. 聚合：把全部低维嵌入聚合到一块，这里就是\(\underset{i=1}{\overset{D}{\sum}}\)

2.聚合变换与NeXt

上面的变换是神经元对输入只进行一次简单内积，现在我们把\(w_ix_1\)换成更一般的函数，当然这个函数也可以是一个子网络。

也就是说，之前是在一个神经元中的变换从内积变成了一堆子网络。

如果Inception是“网络中的网络”（Network-in-Network），那么这里就是“神经元中的网络”（Network-in-Neuron）

\[\mathcal{F}(x)=\underset{i=1}{\overset{C}{\sum}}\mathcal{T}_i(X) \]

其中\(\mathcal{T}_i\) 是能把\(X\)投影到（低维）子空间，并进行变换的任意函数。ResNeXt中，\(\mathcal{T}_i\)是一个自带瓶颈的网络结构（\(1*1\)conv降维→\(3*3\)conv→\(1*1\)conv升维)

\(C\)就是传说中的“基数”了，类比神经元，就和通道数\(D\)差不多。论文发现，基数本身可以作为继卷积滤波器宽度（通道数），网络深度（卷积层数）之后的第三个基本超参数（那种理应越大越好的超参数）。特别是当增长深度与宽度对模型的收益边际递减时，基数的增加另辟蹊径解决了这一问题。

在深度和宽度外找到了第3个维度：基数。模型也因找到了下一个调参维度，而被称为“NeXt”。

最后，加上我们喜闻乐见的恒等映射，就做好ResNeXt的基本结构啦

\[y=X+\underset{i=1}{\overset{C}{\sum}}T_i(X) \]

3.为何要强调“聚合变换”？

很多人看到ResNeXt的介绍/论文时，直到这里都是懵的。（以后看到很多人，自动替换成当年的我就好了）

懵了后只想看图，觉得就像作者吹了半天牛，其实只是把Inception的idea直接照抄过来。

其实不然，作者写这么多非但不是为了把Inception的想法照抄，而是想把Inception从立脚点开始到性能都吊起来打一顿。

img

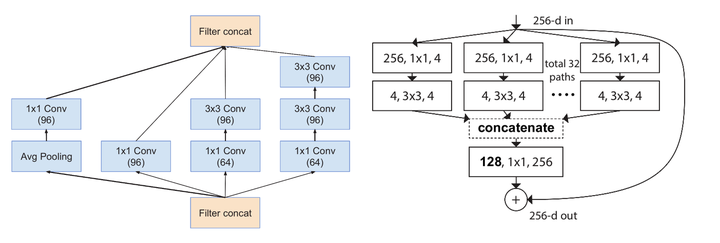
上图左边是Incepytion，右边是ResNeXt。观察两个Block结构，能发现二者有何差别？（除了上下颠倒，除了一个彩色一个黑白……）

最本质的差别，其实是Block内每个分支的拓扑结构，Inception为了提高表达能力/结合不同感受野，每个分支使用了不同的拓扑结构。

而ResNeXt则使用了同一拓扑的分支，即ResNeXt的分支是同构的！

分支是同构的！

分支是同构的！

同构的分支才是问题所在，它从根本上动摇了一个独步江湖几年的经典模型的根基。

同构

因为ResNeXt是同构的，因此继承了VGG/ResNet的精神衣钵：维持网络拓扑结构不变。主要体现在两点：

  1. 特征图大小相同，则涉及的结构超参数相同
  2. 每当空间分辨率/2（降采样），则卷积核的宽度*2（我在Res中写作深度，但还是宽度比较严谨，避免和层数的“深度”产生歧义）。

只不过，ResNeXt通过分析得出的\(\mathcal{T}_i\)，拓展了VGG设计原则：从重复相同大小的层，到重复相同拓扑的滤波器组。

除了更加简洁的设计语言，更简单的调参过程，成品模型迁移中更强的鲁棒性外，同构网络在实现时也很有优势。

1.”过于简单“的实现

现在已经有了无数人的结论，以及很多优秀的开源代码，仔细观察这些“成品”，不难发现ResNeXt的实现意外地简洁，至少远比Inception简洁。

简洁到只要给ResNet加个参数，两个卷积换成3个卷积，每个Block里的\(3*3\)conv换成分组卷积就好了。

如下代码快所示，比较需要注意的就是第8行中的 groups=cardinality

class ResNeXtBottleneck(nn.Module):
 def __init__(self, in_channels, out_channels, stride, cardinality, base_width, widen_factor):
 super(ResNeXtBottleneck, self).__init__()
        width_ratio = out_channels / (widen_factor * 64.)
        D = cardinality * int(base_width * width_ratio)
        self.conv_reduce = nn.Conv2d(in_channels, D, kernel_size=1, stride=1, padding=0, bias=False)
        self.bn_reduce = nn.BatchNorm2d(D)
        self.conv_conv = nn.Conv2d(D, D, kernel_size=3, stride=stride, padding=1, groups=cardinality, bias=False)
        self.bn = nn.BatchNorm2d(D)
        self.conv_expand = nn.Conv2d(D, out_channels, kernel_size=1, stride=1, padding=0, bias=False)
        self.bn_expand = nn.BatchNorm2d(out_channels)
 
        self.shortcut = nn.Sequential()
 if in_channels != out_channels:
            self.shortcut.add_module('shortcut_conv',
                                     nn.Conv2d(in_channels, out_channels, kernel_size=1, stride=stride, padding=0,
                                               bias=False))
            self.shortcut.add_module('shortcut_bn', nn.BatchNorm2d(out_channels))

但，这推导到现在的结构比起来，是不是太简单了点？

2.同构ResNeXt Block的等价形式

在引入等价形式之前，我们再看一下推导聚合变换时的式子：

\[\mathcal{F}(x)=\underset{i=1}{\overset{C}{\sum}}\mathcal{T}_i(X) \]

还有内积时的式子：

\[\mathcal{F}(x)=\underset{i=1}{\overset{D}{\sum}}w_ix_i \]

不知到大家看出什么不同了吗？在于第一个式子的自变量。通项公式中写的是向量\(X\)，但内积中求和的却是向量\(X\)其中一个通道\(x_i\)。

而论文中也明确指出\(\mathcal{T}_i\)， 的作用是：“先把输入分发到（低维)嵌入中，再对第i个嵌入变换”，最后对基数C个变换进行汇总。根据这种最开始的想法，我们能得到第一个ResNeXt Block的结构示意图：

img

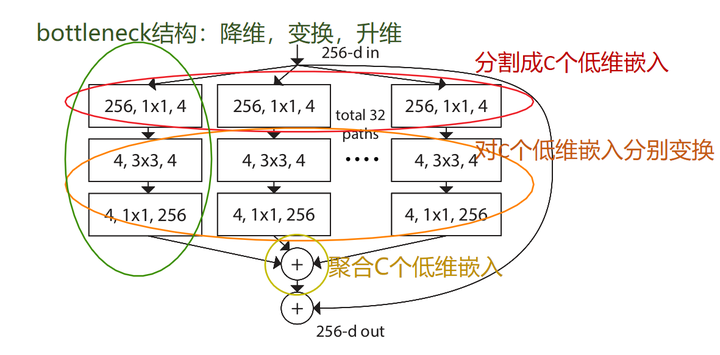
也就是说，如果只看每个Block中单独的支路（Branch），则其只是一个常见的“降维→变换→升维”的Bottleneck结构。但是，若以“分割-变换-聚合”的角度考虑，那么第一个\(1*1\)conv的“降维”，实际上也是把输入分给基数（这里C=32）个低维嵌入的过程。

而在内积中，第一个分割成低维嵌入的过程实际上只是挨个取元素，所以被我们直观忽略了。

img

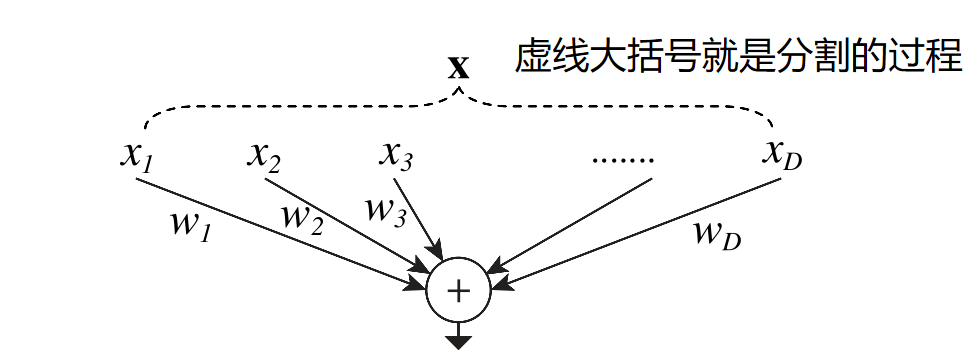
OK，罗嗦这个意义何在？

意义在于让我们知道，分割/汇聚不一定是个显式过程，必要时完全可以等加成更简单的表达。就好比Inception-ResNet形式表示的ResNeXt Block：

img

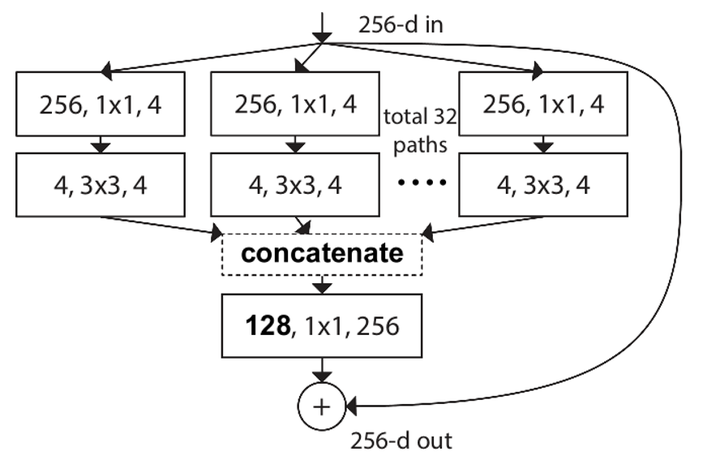
32个输入256通道，输出4通道的\(1*1\)conv加起来，和32个4通道拼在一起变成128通道，再过一个输入128通道输出256通道的\(1*1\)conv有多大区别呢？

我们用MobileNet中计算标准卷积参数量的公式来计算：

\[D_K\cdot D_K\cdot M\cdot N \]

img

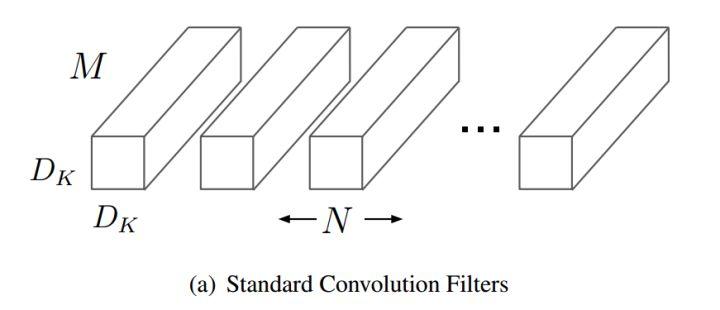
从参数量上：前者为\(32*（1*1*4*256）=32768\)

后者为\(1*1*128*256=32768\)

显然，两者的参数量一样。而Inception早已说明了Block所能表示的解空间，实际上是一个更大卷积核的严格子空间。也就是说，先汇聚后一个大的标准卷积，能表达的范围只会比一堆小的标准卷积之组合更大。因此，这种后者对前者的等价没问题。

那么同理，在最后的32个conv能用上述方法等效成大的conv，那最前面的conv也同理可得一个等效的大conv。那么类似于我在ResNet中提到的滑稽情况（若ResNet的恒等映射中间只有一层权重时，恒等映射加了等于没加）又出现了：

img

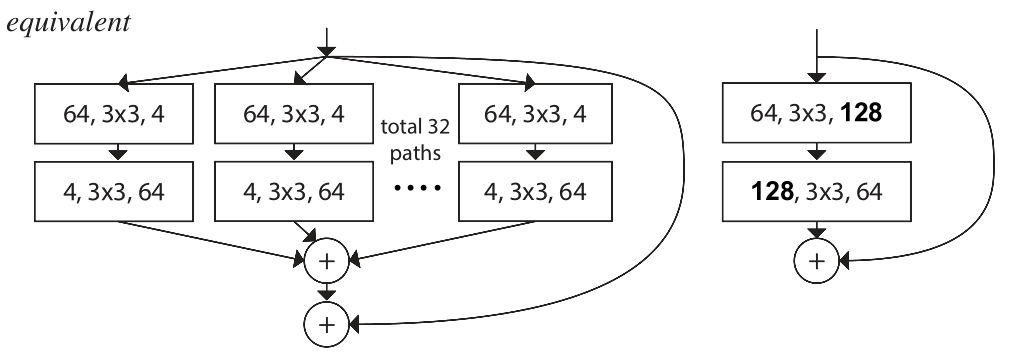
如上图所示，如果一个ResNeXt Block中只有两层conv，前后都可等效成一个大的conv层，那聚合变换和没聚一样。

如果看到这里，你已经完成了对这么个看似很“Inception”，看似很“高大上”的模型祛魅的过程。

因为这种反面例子同样告诉了我们，抛弃重重理论，ResNeXt最核心的地方只存在于被最上最下两层卷积夹着的，中间的部分。和汉堡一样，两边都是面包，中间的肉最值钱。

为什么呢，因为第一个分开的conv其实都接受了一样的输入，各分支又有着相同的拓扑结构。类比乘法结合律，这其实就是把一个conv的输出拆开了分掉。（相同输入，不同输出）

而最后一个conv又只对同一个输出负责，因此就可以并起来用一个conv处理。（不同输入，相同输出）

唯一一个输入和输出都不同的，就是中间的\(3*3\)conv了。它们的输入，参数，负责的输出都不同，无法合并，因此也相互独立。这才是模型的关键所在。

最终模型可以被等效为下图所示的最终形态：

img

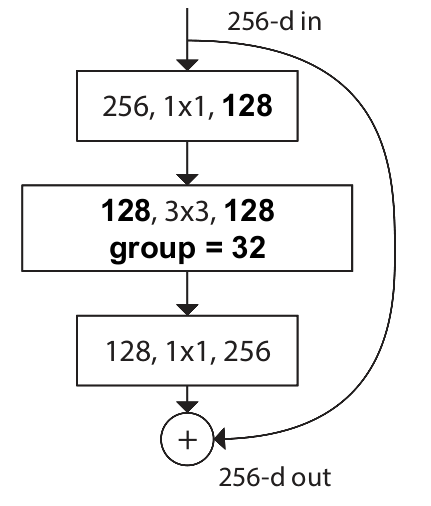
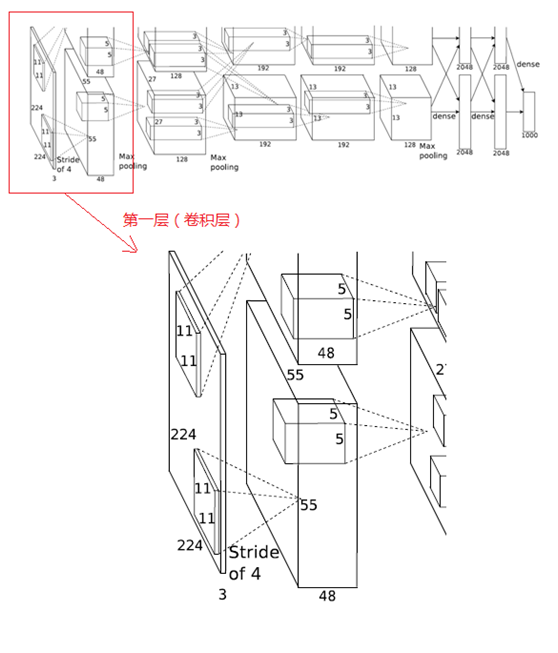
而很巧的是，AlexNet的分组卷积实际上干了一样的事。只不过Alex当时这么做是形势所逼。ResNeXt却是主动选择，还成为了提高模型效果的手段。

img

到这里，同构更大的优势就体现出来了：因为同构，所以经过层层等价，ResNeXt的模型远比Inception来的简洁优雅，易于实现。

模型容量 被遗忘的d

到这里，模型的亮点和特色也差不多了。但是，很多博文都会遗忘掉模型中的另外一个超参数D

self.conv_conv = nn.Conv2d(D, D, kernel_size=3, stride=stride, padding=1, groups=cardinality, bias=False)

就是这段代码的D（论文里为d），它指代C个分支的bottleneck中，降维得到低维嵌入的维度。因此，我们得到最终一个ResNeXt模块的参数量：

\[C\cdot(Inchannel\cdot d+3\cdot 3\cdot d\cdot d+d\cdot Outchannel) \]

可以看出，若d的取值足够小，则模型本身相较ResNet的参数量也不会很大。这就是论文所说的，在保证计算复杂性不变的同时，取得更优结果。

posted @ 2021-10-27 00:08  甫生  阅读(834)  评论(0)    收藏  举报