多项式与生成函数
多项式
多项式乘法
FFT
系数表示法
一个多项式 \(F(x)\) 有多种表示法,最常见的就是系数表示法 \(F(x)=\sum_{i=0}^na_ix^i\)
而这种表示法直接求解多项式的乘法 \(F(x)\times G(x)\) 便是两个求和符号的相乘也就是一个卷积的形式是 \(\sum_{i=0}^{n+m}\sum_{j=0}^ia_jb_{i-j}x^i\)
复杂度为 \(O(n^2)\),非常的慢
点值表示法
一个多项式 \(F(x)\) 为一个 \(n\) 次函数,所以一定可以由 \(n+1\) 个点来确定唯一一个多项式,将这 \(n+1\) 个点写成集合 \(S=\{i\in [0,n]|(x_i,F(x_i))\}\) 就是该多项式的点值表示形式
而改用点值表示后,多项式的相乘便是各项点值的函数值相乘,前提是自变量相对应
但此时时间瓶颈却在求点值表示形式,复杂度仍为 \(O(n^2)\)
若要优化,则只能考虑代入几个好求的 \(x\) 从而加速
单位根
下文中,设 \(n=2^k\)
考虑什么样的 \(x\) 会比较好求,由于跟 \(x\) 有关的都是幂次,所以我们需要找一个 \(x\) 使得它的各个幂次都可以快速得到
对于这样的 \(x\),我们很容易就能想到可以取 \(1\),但是只有这一种取值显然不够用,于是我们不在数轴上取值,而在复平面上取值
在向量中,两个向量的乘法便是模长相乘、辐角相加,而这里我们依然取模长等于 \(1\),而辐角就必须得不同了,所以 \(x\) 的辐角肯定不能为 \(0\),除此之外均可
为了更好的实现,我们取单位圆上的 \(n\) 等分点,即 \(x^0=x^n=1\),令 \(\omega_n^k\) 为单位圆上的 \(n\) 等分点从 \(x\) 正半轴开始,第 \(k+1\) 个点所表示的复数,而值则可以用欧拉公式解决 \(\omega _n^k=(\omega _n^1)^k=cos(k\times\frac{2\pi}{n})+isin(k\times\frac{2\pi}{n})\)
而对于 \(\omega_{2n}^{2k}\) 发现可以将划分成 \(2n\) 份的单位圆,每两块组合拼接,从而变成 \(\omega_n^k\)
快速傅里叶变换
对于一个 \(n-1\) 次的多项式,用 \(n\) 个点就能将它表示出来,所以将 \(\omega_n^k(k\in[0,n)\) 带入多项式 \(F(x)\) 中来求点值表示法
由 \(\omega_{2n}^{2k}=\omega_n^k\) 受到启发,考虑分治求解,将 \(F(x)\) 按下标奇偶性分类,即 \(F(x)=(a_0x^0+a_2x^2+a_4x^4+\dots+a_{n-2}x^{n-2})+(a_1x^1+a_3x^3+a_5x^5+\dots+a_{n-1}x^{n-1})\)
设 \(F_0(x)=(a_0x^0+a_2x^2+a_4x^4+\dots+a_{n-2}x^{n-2})\),\(F_1(x)=(a_1x^1+a_3x^3+a_5x^5+\dots+a_{n-1}x^{n-1})\)
则 \(F(x)=F_0(x^2)+xF_1(x^2)\)
代入 \(\omega_n^k(k<\frac{n}{2})\),\(F(x)=F_0(x^2)+xF_1(x^2)=F_0(\omega_n^{2k})+\omega_n^{k}F_1(\omega_n^{2k})=F_0(\omega_{\frac{n}{2}}^{k})+\omega_n^{k}F_1(\omega_{\frac{n}{2}}^{k})\)
代入 \(\omega_n^{k+\frac{n}{2}}(k<\frac{n}{2})\),\(F(x)=F_0(x^2)+xF_1(x^2)=F_0(\omega_n^{2k+n})+\omega_n^{k+\frac{n}{2}}F_1(\omega_n^{2k+n})=F_0(\omega_{\frac{n}{2}}^{k})-\omega_n^{k}F_1(\omega_{\frac{n}{2}}^{k})\) 由于是在单位圆上取的点,所以 \(\omega_n^k=\omega_n^{k+n}\),而 \(\omega_n^k=-\omega_n^{k+\frac{n}{2}}\) 则是因为两点是关于原点中心对称的,所以互为相反数
观察两个式子,只有中间的符号不一样,所以可以通过第一个式子来算出第二个式子,从而达到规模减半的效果
快速傅里叶逆变换
在上述算法中,最后算出的结果为点值表示法的多项式乘积,而我们一般用的还是系数表示法下的多项式,所以还得将点值表示法转为系数表示法,即傅里叶逆变换
现在已知点至表示法 \(S=\{i\in [0,n)|(\omega_n^i,F(\omega_n^i))\}\),求 \(F(x)\),将其写成矩阵形式
\(\begin{bmatrix} (\omega_n^0)^0 &(\omega_n^0)^1 &(\omega_n^0)^2 &\cdots &(\omega_n^0)^{n-1} \\ (\omega_n^1)^0 &(\omega_n^1)^1 &(\omega_n^1)^2 &\cdots &(\omega_n^1)^{n-1} \\ (\omega_n^2)^0 &(\omega_n^2)^1 &(\omega_n^2)^2 &\cdots &(\omega_n^2)^{n-1} \\ \vdots &\vdots &\vdots &\ddots &\vdots \\ (\omega_n^{n-1})^0 &(\omega_n^{n-1})^1 &(\omega_n^{n-1})^2 &\cdots &(\omega_n^{n-1})^{n-1} \end{bmatrix} \times \begin{bmatrix} a_0 \\ a_1 \\ a_2 \\ \vdots \\ a_{n-1} \end{bmatrix}= \begin{bmatrix} F(\omega_n^0) \\ F(\omega_n^1) \\ F(\omega_n^2) \\ \vdots \\ F(\omega_n^{n-1}) \end{bmatrix}\)
要求系数 \(a\) 就可以将点值 \(F(\omega_n^k)\) 乘上左边矩阵的逆矩阵,而逆矩阵则可以通过待定系数法+高斯消元求得
但求了几组就能发现其实逆矩阵即为
\(\begin{bmatrix} (\omega_n^{-0})^0 &(\omega_n^{-0})^1 &(\omega_n^{-0})^2 &\cdots &(\omega_n^{-0})^{n-1} \\ (\omega_n^{-1})^0 &(\omega_n^{-1})^1 &(\omega_n^{-1})^2 &\cdots &(\omega_n^{-1})^{n-1} \\ (\omega_n^{-2})^0 &(\omega_n^{-2})^1 &(\omega_n^{-2})^2 &\cdots &(\omega_n^{-2})^{n-1} \\ \vdots &\vdots &\vdots &\ddots &\vdots \\ (\omega_n^{-(n-1)})^0 &(\omega_n^{-(n-1)})^1 &(\omega_n^{-(n-1)})^2 &\cdots &(\omega_n^{-(n-1)})^{n-1} \end{bmatrix}=\begin{bmatrix} (\omega_n^0)^0 &(\omega_n^0)^1 &(\omega_n^0)^2 &\cdots &(\omega_n^0)^{n-1} \\ (\omega_n^{n-1})^0 &(\omega_n^{n-1})^1 &(\omega_n^{n-1})^2 &\cdots &(\omega_n^{n-1})^{n-1} \\ (\omega_n^{n-2})^0 &(\omega_n^{n-2})^1 &(\omega_n^{n-2})^2 &\cdots &(\omega_n^{n-2})^{n-1} \\ \vdots &\vdots &\vdots &\ddots &\vdots \\ (\omega_n^1)^0 &(\omega_n^1)^1 &(\omega_n^1)^2 &\cdots &(\omega_n^1)^{n-1} \end{bmatrix}\)
将正常做的傅里叶变换的 \([1,n)\) 区间中的数整体翻转一下即可
代码
递归直接按上面说的写就行,这里只放非递归
class polynomial{
private:
const ld pie = acos(-1);
struct complex{
ld x, y;
inline complex operator + (complex t){
return complex{x + t.x, y + t.y};
}
inline complex operator - (complex t){
return complex{x - t.x, y - t.y};
}
inline complex operator * (complex t){
return complex{x * t.x - y * t.y, x * t.y + y * t.x};
}
};
int id[N + 10];
inline void fft(const int n, const complex *a, complex *b){
for(int i = 0; i < n; i++){
if(i <= id[i]){
complex x = a[i], y = a[id[i]];
b[i] = y, b[id[i]] = x;
}
}
for(int len = 1; len < n; len <<= 1){
complex w{cos(pie / len), sin(pie / len)}, wi;
for(int i = 0; i < n; i += (len << 1)){
wi = {1, 0};
for(int j = 0; j < len; j++, wi = wi * w){
complex x = b[i + j], y = wi * b[i + j + len];
b[i + j] = x + y;
b[i + j + len] = x - y;
}
}
}
}
public:
inline void mul(const int n, const int *a, const int m, const int *b, int *c){
static complex f[N + 10];
for(int i = 0; i <= n; i++)
f[i].x = a[i];
for(int i = 0; i <= m; i++)
f[i].y = b[i];
int fnn = __lg(n + m) + 1, len = 1 << fnn;
for(int i = 0; i < len; i++)
id[i] = (id[i >> 1] >> 1) | ((i & 1) << (fnn - 1));
fft(len, f, f);
for(int i = 0; i < len; i++)
f[i] = f[i] * f[i];
fft(len, f, f);
reverse(f + 1, f + len);
for(int i = 0; i <= n + m; i++)
c[i] = f[i].y / (len << 1) + 0.5;
for(int i = max(n, m) + 1; i <= len; i++)
f[i] = {0, 0};
}
} poly;
例题
- 【模板】多项式乘法(FFT)
- [ZJOI2014] 力
- 将原式拆成两部分,分开求解
- 发现拆开后的式子为 \(q\) 数组除以一个距离数组,而这两个数组正好是卷积的形式,直接 \(fft\) 优化即可
- 注意,三次 \(fft\) 的精度更高
NTT
在有模数的情况下 \(FFT\) 一般都不适用,原因则是利用了单位根及单位圆的性质,但是单位圆上的复数均不为整数,考虑是否还有其他的 \(x\) 可以代替单位根
最主要的还是得代替掉 \(\omega_n^1\) 其他都可以由它的幂次得来,考虑找一个数满足 \(\omega\) 的性质,最基本的定义便是 \((\omega_n^1)^n=1,\forall i\in[0,n),(\omega_n^1)^i\not=1\) 满足该定义,即为单位根
由费马小定理,若模数 \(p\) 为质数,则 \(x^{p-1}\equiv 1(mod\ p)\Rightarrow x^{p-1}\equiv x^0(mod\ p)\Rightarrow (x^{\frac{p-1}{n}})^n\equiv x^0(mod\ p)\) 所以若把 \(x^{\frac{p-1}{n}}\) 作为 \(\omega\) 的替代品,则还需要满足它的其他比 \(n\) 小的次方不等于 \(1\),那我们只要让 \(x\) 在 \(i\in [1,p),x^i取便[1,p)(mod\ p)\) 即可保证 \(1\) 只有一个次幂使该替代品可以取到,即可满足单位根的定义
而满足上述性质的 \(x\) 即为原根,同时还得保证 \(n|p-1\) 因为 \(x^{\frac{p-1}{n}}\) 不能是小数
注:\(998244353\) 的原根为 \(3\)
代码
大致跟 \(FFT\) 一样,只是不能三遍 \(FFT\) 变两遍
class polynomial{
private:
int id[N + 10];
inline void ntt(int n, const int *a, int *b){
for(int i = 0; i < n; i++){
if(i <= id[i]){
int x = a[i], y = a[id[i]];
b[i] = y, b[id[i]] = x;
}
}
for(int len = 1; len < n; len <<= 1){
int w = pow(3, (mod - 1) / (len << 1));
for(int i = 0; i < n; i += (len << 1)){
int wi = 1;
for(int j = 0; j < len; j++, wi = 1ll * wi * w % mod){
int x = b[i + j], y = 1ll * wi * b[i + j + len] % mod;
b[i + j] = add(x, y), b[i + j + len] = sub(x, y);
}
}
}
}
public:
inline void mul(int n, const int *a, int m, const int *b, int *c){
int fnn = __lg(n + m) + 1, len = 1 << fnn;
for(int i = 0; i < len; i++)
id[i] = (id[i >> 1] >> 1) | ((i & 1) << (fnn - 1));
static int f[N + 10], g[N + 10];
for(int i = 0; i < len; i++)
f[i] = i <= n ? a[i] : 0;
ntt(len, f, f);
for(int i = 0; i < len; i++)
g[i] = i <= m ? b[i] : 0;
ntt(len, g, g);
for(int i = 0; i < len; i++)
f[i] = 1ll * f[i] * g[i] % mod;
ntt(len, f, f);
reverse(f + 1, f + len);
int inv = pow(len, mod - 2);
for(int i = 0; i <= n + m; i++)
c[i] = 1ll * f[i] * inv % mod;
}
} poly;
例题
- 【模板】多项式乘法(FFT)
- [AH2017/HNOI2017] 礼物
- 由于 \(c\) 可以加在两条项链中的任意一个上,所以对 \(x_i-y_i\) 的贡献便是 \(+c\)(加在 \(x\) 上)或 \(-c\)(加在 \(y\))上,所以 \(c\) 对 \(x_i-y_i\) 的贡献值域变不只是非负数而是 \(\R\)
- 式子题先来化式子 \(\sum_{i=1}^n(x_i-y_i+c)^2=\sum_{i=1}^nx_i^2+y_i^2+c^2+2(-x_iy_i+x_ic-y_ic)\),\(x_i^2\) 和 \(y_i^2\) 都是常数项可以直接加入答案,再将与 \(c\) 有关的提出来 \(\sum_{i=1}^nc^2+2c(x_i-y_i)\) 化简 \(nc^2+2(\sum_{i=1}^nx_i-y_i)c\),由于 \(c\) 的一次项为常数(设为 \(S\))所以这是个开口向上的二次函数,当 \(c\) 取到对称轴直线 \(c=-\frac{S}{2n}\) 时函数为最小值,所以 \(c\) 直接取距离对称轴最近的一个整数值即可
- 剩下的式子便是 \(-2\sum_{i=1}^nx_iy_i\),\(x\) 不转 \(y\) 转,所以环上问题将 \(y\) 倍长,此时便是 \(x\) 与 \(y^{'}\) 的平行积,平行积都可以通过翻转从而转成卷积,所以翻转 \(x\),将 \(x\) 与 \(y\) 左端对齐,\(x\) 的剩下 \(n\) 个位置赋 \(0\),此时两个序列的卷积的结果恰好就是所有平行积的结果
分治FFT
对于形如 \(f_i=\sum_{j=0}^{i-1}f_jg_{i-j}\) 的递推式,普通的多项式乘法并不可做,而这种前面状态影响后面状态的 \(dp\) 我们多半可以考虑 \(cdq\) 分治来整体 \(dp\)
对于一层 \(cdq\),左边的答案已经在之前递归进来就处理好外部的答案,所以只需要继续递归进内部计算内部答案,而右边还可以由左边来计算,所以得先用左边已经算好的 \(f\) 做个卷积将答案加到右边才能继续递归进右边计算内部答案
代码
void cdq(int L, int R){
if(L == R)
return;
int mid = (L + R) >> 1;
cdq(L, mid);
int fnn = __lg(mid - L + R - L) + 1, len = 1 << fnn;
for(int i = 0; i < len; i++)
a[i] = b[i] = 0;
for(int i = L; i <= mid; i++)
a[i - L] = f[i];
for(int i = 0; i <= R - L; i++)
b[i] = g[i];
for(int i = 0; i < len; i++)
id[i] = (id[i >> 1] >> 1) | ((i & 1) << (fnn - 1));
ntt(len, a, 1);
ntt(len, b, 1);
for(int i = 0; i < len; i++)
a[i] = 1ll * a[i] * b[i] % mod;
ntt(len, a, -1);
for(int i = 1; i <= R - mid; i++)
f[mid + i] = add(f[mid + i], 1ll * a[i + (mid - L)] * pow(len, mod - 2) % mod);
cdq(mid + 1, R);
}
例题
任意模数多项式乘法
这里有模数所以只能用 \(NTT\),但 \(NTT\) 的模数必须保证 \(n|p-1\) 其中 \(n\) 为一个比输入多项式次数大的 \(2^k\),这个显然局限性非常大,如何不用考虑这个限制呢
因为题目要求任意模数,所以干脆不要模数了,但是不用模数 \(NTT\) 就得写高精度,所以不能不要模数,那如何达到不取模的效果呢,直接让模数大于 \(maxans\) 好了,这样对于 \(ans\) 来说并没有取模,但确实有模数存在
但是此时一般都需要开到 \(int128\) 或者根本开不下还得写高精度,所以有什么办法能把小的模数变大还能通过小模数下的答案算出大模数下的答案呢,这里已经比较明显了,满足条件的只有 \(EXCRT\),它的模数为 \(lcm\),这已经非常大了,完全够用,而我们只需要求几次不同模数的 \(NTT\) 得到一个同余方程组,即可利用 \(EXCRT\) 算出在模 \(lcm\) 意义下的答案,此时答案即为原本答案,再取个题目给定的模数即可
代码
这里的 \(ntt(n,*a,*f,mod)\) 函数表示的是长度为 \(n\)、系数为 \(a\)、点值返回到 \(f\)、s模数为 \(mod\)
for(int i = 0; i < 3; i++){
ntt(len, a, f, mod[i]);
ntt(len, b, g, mod[i]);
for(int j = 0; j < len; j++)
f[j] = 1ll * f[j] * g[j] % mod[i];
ntt(len, f, h[i], mod[i]);
reverse(h[i] + 1, h[i] + len);
for(int j = 0; j < len; j++)
h[i][j] = 1ll * h[i][j] * pow(len, mod[i] - 2, mod[i]) % mod[i];
}
for(int i = 0; i <= n + m; i++){
__int128 a = h[0][i], b = mod[0];
for(int j = 1; j < 3; j++){
__int128 x, y;
exgcd(b, mod[j], x, y);
a += x * (h[j][i] - a) % mod[j] * b;
b *= mod[j];
a = (a % b + b) % b;
}
cout << a % p << ' ';
}
例题
多项式乘法逆
题目即求一个 \(G(x)\) 满足 \(1.G(x)\equiv \frac{1}{F(x)}(mod\ x^n)\) 化式子即可
同样考虑分治减少时间复杂度,设 \(2.H(x)\equiv \frac{1}{F(x)}(mod\ x^{\frac{n}{2}})\)
则 \(1\) 式减 \(2\) 式为 \(G(x)-H(x)\equiv 0(mod\ x^{\frac{n}{2}})\)
同时平方 \((G(x)-H(x))^2\equiv0(mod\ x^n)\)
化简 \(G^2(x)+H^2(x)-2GH(x)\equiv0(mod\ x^n)\)
因为 \(F(x)*G(x)=1\),所以同时乘上 \(F(x)\) 来化简,\(G(x)+FH^2(x)-2H(x)\equiv 0(mod\ x^n)\)
移项,\(G(x)\equiv2H(x)-FH^2(x)(mod\ x^n)\) 就得到了 \(G(x)\) 的递推式,倍增求解即可
代码
inline void inv(int n, const int *a, int *b){
int fnn = __lg(n) + 1, len = 1 << fnn;
b[0] = pow(a[0], mod - 2);
for(int i = 2; i <= len; i <<= 1){
static int f[N + 10];
mul(i - 1, a, i - 1, b, f);
mul(i - 1, f, i - 1, b, f);
for(int j = 0; j < i; j++)
b[j] = sub(add(b[j], b[j]), f[j]);
}
}
例题
多项式对数函数
求 \(G(x)=ln(F(x))(mod\ p)\)
微分/导数
- 基本求导公式:\(f'(x)=\lim_{h \to 0} (f(x+h)-f(x))/h\) 即,函数 \(f\) 在横坐标为 \(x\) 处的切线斜率,用于表示函数的变化速率,类似加速度
- 常数求导:\(f(x)=a,f'(x)=0\)
- 幂函数求导:\(f(x)=x^a,f'(x)=ax^{a-1}(a\in R)\)
- 指数函数求导:\(f(x)=a^x,f'(x)=a^xlna,(a>0,a\not=1)\)
- 特别的,以 \(e\) 为底的指数函数求导:\(f(x)=e^x,f'(x)=e^x\)
- 对数函数求导:\(f(x)=log_ax,f'(x)=\frac{1}{xlna},(a>0,a\not=1)\)
- 特别的,自然对数函数的求导:\(f(x)=lnx,f'(x)=\frac{1}{x}\)
- 三角函数的求导:
- \(sin'(x)=cos(x)\)
- \(cos'(x)=-sin(x)\)
- \(tan'(x)=sec^2(x)\)
- \(cot'(x)=-cec^2(x)\)
- \(sec'(x)=sec(x)tan(x)\)
- \(csc'(x)=-csc(x)cot(x)\)
- 导数的四则运算
- \((f(x)+g(x))'=f'(x)+g'(x)\)
- \((f(x)-g(x))'=f'(x)-g'(x)\)
- \((f(x)g(x))'=f'(x)g(x)+f(x)g'(x)\)
- \((\frac{f(x)}{g(x)})'=\frac{(f'(x)g(x)-f(x)g'(x))}{g^2(x)}\)
- 复合函数求导(链式法则)
- \((f_1(f_2(f_3(\dots))))'=\prod_{i=1}f_i'(\prod_{j>i}f_j(x))\) 等号左边即为求整个复合函数的导数,而右边的则可以先求出 \(f_i\) 的导数,再将里面的累乘结果当作自变量代入,区别则在于整体求导的时候不能先将函数的值作为自变量代入
积分
积分即为将微分后的值给累加起来,而累加起来后显然就是微分前的原数,所以积分即为微分和导数的逆运算,公式也就是将上述的求导公式作个逆运算即可
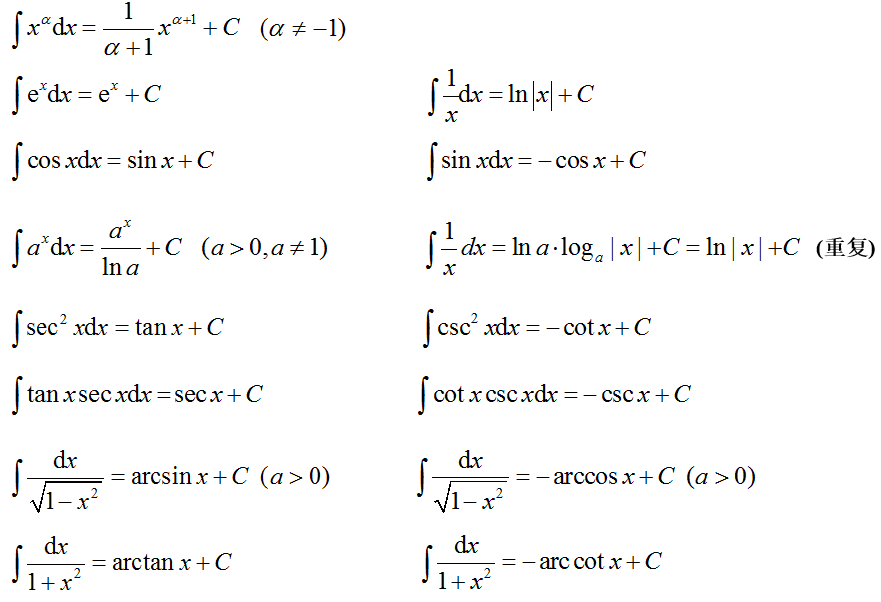
因为常数的导数为 \(0\),所以求完导之后我们并不知道常数项是多少,因此我们在积分还原的时候加上一个常数项 \(C\) 即可,而 \(C\) 是不确定的,所以这也叫不定积分
求解
回到题目上,\(ln\) 函数并不好求,我们考虑对等式两边同时求导 \(G'(x)=(ln(F(x)))'(mod\ p)\)
将 \(ln\) 看作一个函数,则等式右边即为一个复合函数的求导,使用链式法则 \(G'(x)=ln'(F(x))*F'(x)\)
化简 \(G'(x)=\frac{1}{F(x)}*F'(x)\)
多项式求导运用幂函数求导即可,算出 \(G'(x)\) 再用积分积起来
代码
inline void ln(int n, const int *a, int *b){
static int f[N + 10], g[N + 10];
for(int i = 0; i < n; i++)
f[i] = 1ll * a[i + 1] * (i + 1) % mod;
f[n] = 0;
inv(n, a, g);
mul(n, f, n, g, b);
for(int i = n; i >= 1; i--)
b[i] = 1ll * b[i - 1] * pow(i, mod - 2) % mod;
b[0] = 0;
}
例题
多项式指数函数
泰勒展开
对于任意函数 \(f(x)\),若要将它转为多项式形式,则需要运用泰勒展开
对于函数 \(f(x)\) 在 \(x_0\) 处的泰勒展开结果为 \(\sum_{i=0}^n\frac{f^{(i)}(x_0)}{i!}(x-x_0)^i\),展开项越多(\(n\) 越大,前提是原函数有 \(n\) 阶导),该多项式越逼近与原函数
如果我们在 \(x_0=0\) 处展开,此时便是麦克劳林展开:\(\sum_{i=0}^n\frac{f^{(i)}(0)}{i!}x^i\)
可以这么记忆:麦克劳林即为序列 \(<f^{(i)}(0)>\) 的 \(EGF\),而泰勒展开则是将 \(0\) 变为了 \(x_0\),以及将 \(x^i\) 变为 \((x-x_0)^i\)
牛顿迭代
牛顿迭代是用于求解函数 \(0\) 点的方法,而这里要用到的是多项式牛顿迭代
设要求多项式 \(G(x)\) 的零点,假设零点为多项式 \(F(x)\) 则 \(G(F(x))\equiv0(mod\ x^n)\)
同样考虑分治处理,设已经求出 \(G(F_0(x))\equiv0(mod\ x^{\frac{n}{2}})\),考虑如何扩展到 \((mod\ x^n)\)
对于多项式 \(G(F(x))\) 在 \(F_0(x)\) 处泰勒展开,则 \(G(F(x))=\sum_{i=0}^n\frac{G^{(i)}(F_0(x))}{i!}(F(x)-F_0(x))^i\)
而因为 \(F_0(x)\) 为 \(F(x)\) 的前 \(\frac{n}{2}\) 项,所以它们相减后所得的多项式的前 \(\frac{n}{2}\) 项为 \(0\),所以 \((F(x)-F_0(x))^2\) 的前 \(n\) 项也为 \(0\),即 \((F(x)-F_0(x))^2\equiv 0(mod\ x^n)\),所以当 \(i\ge 2\) 时,\((F(x)-F_0(x))^i=0\),所以只用看展开式的前两项
即 \(G(F(x))\equiv G(F_0(x))+G^{'}(F_0(x))(F(x)-F_0(x))(mod\ x^n)\)
又因为 \(G(F(x))=0\) 所以 \(F(x)\equiv F_0(x)-\frac{G(F_0(x))}{G^{'}(F_0(x))}(mod\ x^n)\)
求解
要求解 \(G(x)\) 使 \(G(x)=e^{F(x)}\)
先给两边同时取 \(ln\),\(ln(G(x))=F(x)\Rightarrow ln(G(x))-F(x)=0\)
将等号左边看作多项式函数 \(H(G(x))\),在多项式函数中,\(F(x)\) 已知所以为常数项,而 \(G(x)\) 为自变量,现在即为求解 \(H(G(x))\) 的零点
对于 \(H(G(x))\) 求导,\(H^{'}(G(x))=\frac{1}{G(x)}\)
带入多项式牛顿迭代中,\(G(x)=G_0(x)-G_0(x)(ln(G_0(x))-F(x))\) 化简为 \(G(x)=G_0(x)(1-ln(G_0(x))+F(x))\)
代码
inline void exp(const int n, const int *a, int *b){
static int f[N + 10];
b[0] = 1;
for(int t = 1; t <= __lg(n) + 1; t++){
ln((1 << t) - 1, b, f);
for(int i = 0; i < (1 << t); i++)
f[i] = sub(a[i], f[i]);
f[0] = add(f[0], 1);
mul((1 << t) - 1, f, (1 << t) - 1, b, b);
memset(f, 0, (1 << t) << 2);
}
memset(f, 0, (1 << (__lg(n) + 1)) << 2);
memset(b + n + 1, 0, (1 << (__lg(n) + 2)) << 2);
}
例题
多项式快速幂
要快速求解多项式 \(F(x)\) 的 \(k\) 可以直接类比整数快速幂,从而做到 \(O(nlog^2n)\)
但这个还是太慢了,考虑将运算降级,从通过取 \(ln\) 将运算从乘方降为乘法,这种降级思想后面还会用到
现在 \(F^k(x)\) 就变成了 \((e^{lnF(x)})^k=e^{klnF(x)}\) 运用多项式对数函数和指数函数即可
对于强化版,题目并不再保证 \([x^0]F(x)=1\) 了,所以考虑将它变为 \(1\),于是将所有系数同除 \([x^0]F(x)\),即 \(F^k(x)=(\sum_{i=0}^nf_ix^i)^k=(f_0\sum_{i=0}^n\frac{f_i}{f_0}x^i)^k=(\sum_{i=0}^n\frac{f_i}{f_0}x^i)^kf_0^k\)
然而,这是在 \(f_0\not=0\) 情况下的化简,对于 \(f_0=0\) 的情况,多项式的第一项因为系数为 \(0\) 所以不用写出来,即 \(F(x)=\sum_{i=1}^nf_ix^i\),提出来一个 \(x\),\(F(x)=x\sum_{i=0}^{n-1}f_{i+1}x^i\),同理,按照此思想,找到第一个不为 \(f_i\not=0\) 使其成为多项式的常数项,即可运用上面的式子化简
代码
inline void polypow(const int n, int *a, int k, int *b){
int inv = pow(a[0], mod - 2), a0 = a[0];
for(int i = 0; i <= n; i++)
a[i] = 1ll * a[i] * inv % mod;
static int f[N + 10];
ln(n, a, f);
for(int i = 0; i <= n; i++)
f[i] = 1ll * f[i] * k % mod;
exp(n, f, b);
memset(f, 0, (n + 5) << 2);
int pw = pow(a0, kkk);
for(int i = 0; i <= n; i++)
b[i] = 1ll * b[i] * pw % mod;
}
例题
- 差分与前缀和
- 考虑用多项式来表示做前缀和的过程,发先将原多项式乘上一个系数全为 \(1\) 的多项式即为求一次前缀和,同理乘上一个 \(1-x\) 即为求一次差分,跟矩阵的用法极为相似
- 所以类比矩阵,用多项式快速幂加速该过程
生成函数
OGF
普通生成函数(\(ordinary\ generating\ function,OGF\)),用来表示一个序列,在多重集组合计数或无标号计数问题中常用
序列 \(f\) 的普通生成函数定义为形式幂级数:\(F(x)=\sum_{i=0}^nf_ix^i\)
序列 \(f\) 既可以是有穷也可以是无穷
基本运算
生成函数的加减法即为对应次数的系数相加减
考虑乘法,生成函数 \(F(x)\) 与 \(G(x)\) 的乘法为 \(F(x)G(x)=\sum_{i=0}^nf_ix^i\sum_{j=0}^mg_jx^j=\sum_{i=0}^{n+m}x^i\sum_{j=0}^if_jg_{i-j}\)
生成函数的乘法即为多项式乘法,也就是卷积
其组合意义就是 \(f_i\) 为从集合 \(A\) 中选取 \(i\) 个元素的方案数,\(g_j\) 为从集合 \(B\) 中选取 \(j\) 个元素的方案数,而两者的生成函数相乘后的新生成函数设为 \(H(x)\),则 \(h_k\) 表示从 \(A\) 和 \(B\) 集合中共选出 \(k\) 个元素的方案数,若将乘数增多,便成为了多重集组合,更通俗的说就是背包问题
封闭形式
举个例子,生成函数 \(F(x)=\sum_{i=0}^{\infty}x^i\) 的封闭形式为 \(\frac{1}{1-x}\) 因为 \(xF(x)=\sum_{i=1}^{\infty}x^i\Rightarrow F(x)-xF(x)=1\Rightarrow F(x)=\frac{1}{1-x}\)
用封闭形式来表示生成函数在某些时候会大大减小计算量
常用封闭形式
- \(F(x)=\sum_{i=0}^{\infty}ap^ix^i=\frac{a}{1-px}\) 即等比数列的封闭形式
- \(F_v(x)=\sum_{i=0}^{\infty}x^{vi}=\frac{1}{1-x^v}\) 即完全背包中一个体积为物品为 \(v\) 放入背包的方案的生成函数的封闭形式
- \(F_n(x)=\sum_{i=0}^{n}\binom{n}{i}x^i=(1+x)^n\) 即杨辉三角第 \(n\) 层的封闭形式
例题
-
- 背包是典型的无标号计数问题,普通的背包 \(dp\) 已经无法优化,所以考虑多项式求解
- 对于每种物品,可以写出其对应的生成函数,体积为 \(v\) 的物品的生成函数为 \(F_v(x)=\sum_{i=0}^{\infty}x^{vi}=\frac{1}{1-x^v}\)
- 多种物品的生成函数相乘就得到了答案数组的生成函数,答案即为该生成函数的 \(m\) 次项的系数
- 考虑如何求解该生成函数,答案生成函数为 \(G(x)=\prod_vF_v(x)=\prod_v\frac{1}{1-x^v}\)
- 由于是累乘,计算量太大,考虑对于每个 \(F_v(x)\) 取 \(ln\) 转为求和 \(G(x)=e^{\sum_vln\frac{1}{1-x^v}}\)
- 对于 \(ln\frac{1}{1-x^v}\),这个多项式可以通过大表来找规律,也可以直接背结论,\(ln\frac{1}{1-x^v}=\sum_{i=1}^{\infty}\frac{1}{i}x^{vi}\)
- 所以直接在调和级数的时间内预处理 \(e\) 的指数上的多项式,然后套多项式指数函数即可
-
-
法一:
-
划分类问题考虑定下来第一个划分出来的元素,然后将剩下元素转为子问题递推解决,这道题则定 \(a_1\),而定下来 \(a_1\) 后即可把 \(a_1\) 提出来,即可列出答案的递推式(设答案为 \(g\)):\(g_i=\sum_{j=1}^if_jg_{i-j}\)
-
此时还是不好做,考虑将上式中的斐波那契拆开:\(g_i=\sum_{j=1}^i(f_{j-1}+f_{j-2})g_{i-j}\)
-
化简、变形:
-
\(g_i=\sum_{j=1}^if_{j-1}g_{i-j}+\sum_{j=1}^if_{j-2}g_{i-j}\)
-
\(g_i=\sum_{j=0}^{i-1}f_jg_{i-j-1}+\sum_{j=-1}^{i-2}f_jg_{i-j-2}\)
-
\(g_i=\sum_{j=1}^{(i-1)}f_jg_{(i-1)-j}+f_0g_{i-1}+\sum_{j=1}^{(i-2)}f_jg_{(i-2)-j}+f_{-1}g_{i-1}+f_0g_{i-2}\)
-
观察可得两个求和符号跟定义式是一样的:\(g_i=g_{i-1}+g_{i-2}+f_0g_{i-1}+f_0g{i-2}+f_{-1}g_{i-1}\)
-
因为 \(f_2=f_1+f_0\) 且 \(f_1=f_2=1\) 解方程可得 \(f_0=0\) 同理 \(f_{-1}=1\)
-
代入上式:\(g_i=2g_{i-1}+g_{i-2}\)
-
-
此 \(2\) 阶递推式可以用生成函数或者特征方程求解其通项
-
生成函数求解:
- 将 \(g\) 序列的普通生成函数写出:\(\sum_{i=0}^{\infty}g_ix^i\)
- 考虑求出其封闭形式:
- 设 \(S=\sum_{i=0}^{\infty}g_ix^i\)
- 则 \(2xS=\sum_{i=1}^{\infty}2g_{i-1}x^i\)、\(x^2S=\sum_{i=2}^{\infty}g_{i-2}x^i\)
- 所以 \(S-g_0-g_1x=2xS-2g_0x+x^2S\) 即 \(S=2xS+x^2S+x\)
- 所以 \(S=\frac{x}{1-2x-x^2}\) 即为原生成函数的封闭形式
- 考虑类比求解斐波那契数列通项的方法,对上式封闭形式拆为两个等比数列的生成函数相加(等比数列的生成函数见上文)
- 具体的:
- 利用待定系数法:\(\frac{a_1}{1-p_1x}+\frac{a_2}{1-p_2x}=\frac{x}{1-2x-x^2}\)
- 所以 \(\left\{\begin{matrix} -p_1-p_2=-2 \\ p_1p_2=-1 \\ a1+a2=0 \\ -a_1p_2-a_2p_1=1 \end{matrix}\right.\)
- 解得 \(\left\{\begin{matrix} a_1=\frac{\sqrt{2}}{4} \\ a_2=-\frac{\sqrt{2}}{4} \\ p_1=1+\sqrt{2} \\ p_2=1-\sqrt{2} \end{matrix}\right.\)
- 所以 \(\sum_{i=0}^{\infty}g_ix^i=\sum_{i=0}^{\infty}\frac{\sqrt{2}}{4}(1+\sqrt{2})^ix^i+\sum_{i=0}^{\infty}-\frac{\sqrt{2}}{4}(1-\sqrt{2})^ix^i\)
- 即 \(g_n=\frac{\sqrt{2}}{4}[(1+\sqrt{2})^n-(1-\sqrt{2})^n]\)
-
-
法二:
- 题目说要划分 \(m\) 个数,但是 \(m\) 并不确定,则可以考虑枚举一下 \(m\)
- 枚举后问题就变成了选 \(m\) 个 \(a_i\) 使其和恰好等于 \(n\),这很像背包问题,更像 \(OGF\) 的组合意义,所以考虑生成函数求解
- 用生成函数表示斐波那契数列,设为 \(F(x)\),选 \(m\) 个数则为相乘 \(m\) 次,即 \(F^m(x)\)
- 所以答案就是 \([x^n]\sum_{m=1}^nF^m(x)\)
- 求和符号求的是一个等比数列之和,只是公比是个多项式,所以上式等于 \(\frac{1}{1-F(x)}\)
- 利用上文方法求解出斐波那契数列的封闭形式,代入化简后为 \(\frac{1-x-x^2}{1-2x-x^2}\)
- 分子分母分开求解,求解方法即为法一后半部分
-
EGF
指数生成函数(\(exponential\ generating\ function,EGF\)),在多重集组合或有标号计数问题中常用
序列 \(f\) 的指数生成函数定义为形式幂级数:\(\hat{F(x)}=\sum_{i=0}^nf_i\frac{x^i}{i!}\)
基本运算
\(\hat{F(x)}\hat{G(x)}=\sum_{i=0}^nf_i\frac{x^i}{i!}\sum_{j=0}^mg_j\frac{x^j}{j!}\)
\(=\sum_{i=0}^{n+m}x^i\sum_{j=0}^if_jg_{i-j}\frac{1}{j!(i-j)!}\)
\(=\sum_{i=0}^{n+m}\frac{x^i}{i!}\sum_{j=0}^if_jg_{i-j}\binom{i}{j}\)
其组合意义便是从 \(A\) 集合中选出 \(i\) 个元素的方案数为 \(f_i\),从 \(B\) 集合中选出 \(j\) 个元素的方案数为 \(g_j\),而相乘后得到的生成函数设为 \(H(x)\), \(h_k\) 则表示从 \(A\) 和 \(B\) 集合中共选出 \(k\) 个且选出的元素之间顺序不同方案也不同,即选出来的元素有标号,若乘数变多,便成为了多重集排列
从定义式角度来证明上面的组合意义,\([x^k]H(x)=\sum_{j=0}^kf_jg_{k-j}\binom{k}{j}\),求和附号后面两项很好理解,要一共选出 \(k\) 元素,那就先枚举第一个集合选几个,然后将从两个集合选数的方案乘起来,接下来就是考虑顺序对于方案数的影响了,首先 \(k\) 个数一共有 \(k!\) 种放法,但是由于这 \(k\) 个数里有重复元素,所以这 \(k!\) 中方案里有重复的方案,于是考虑去重,只需要将每种重复元素内部取个重即可,即除以 \(j!\) 和 \((k-j)!\) 与前面的 \(k!\) 合起来就是 \(\binom{k}{j}\) 所以这里的组合数并不是从 \(k\) 个数中选 \(j\) 个的意思
封闭形式
-
序列 \(<1,1,1,\dots >\) 的 \(EGF\) 是 \(\sum_{i=0}^{\infty}\frac{x^i}{i!}=e^x\)
-
类似的,等比数列 \(<1,p,p^2,\dots>\) 的 \(EGF\) 是 \(\sum_{i=0}^{\infty}p^i\frac{x^i}{i!}=e^{px}\),将 \(p^ix^i\) 看作一个整体代入 \(1\) 式中的 \(x\) 即可
-
序列 \(<1,-1,1,\dots>\) 的 \(EGF\) 是 \(\sum_{i=0}^{\infty}(-1)^i\frac{x^i}{i!}=e^{-x}\),将 \((-1)^ix^i\) 看作一个整体代入 \(1\) 式中的 \(x\) 即可
-
序列 \(<1,0,1,0,\dots>\) 的 \(EGF\) 用 \(1\) 式加上 \(3\) 式再除以 \(2\) 即可,为 \(\frac{e^x+e^{-x}}{2}\)
-
类比组合数的 \(OGF\),排列数的 \(EGF\) 为 \(\sum_{i=0}^{n}n^{\underline{i}}\frac{x^i}{i!}=\sum_{i=0}^n\binom{n}{i}x^i=(x+1)^n\)
-
由于 \(ln(x+1)\) 的麦克劳林展开式为 \(\sum_{i=1}^{\infty}(-1)^{i-1}(i-1)!\frac{x^i}{i!}=\sum_{i=1}(-1)^{i-1}\frac{x^i}{i}\) 所以序列 \(<1,-\frac{1}{2},\frac{1}{3},-\frac{1}{4},\dots>\) 的 \(EGF\) 封闭形式为 \(ln(x+1)\)
-
同理,序列 \(<1,\frac{1}{2},\frac{1}{3},\frac{1}{4},\dots>\) 的 \(EGF\) 封闭形式为 \(-ln(1-x)\)
\(EGF\) 中多项式 \(exp\) 的组合意义
先说结论,对于一个序列 \(f\) 的指数生成函数 \(\hat F(x)\),其中 \(f_i\) 表示具有 \(i\) 个元素所能构成的“集合”方案数(这里由于“集合”的构成不同,方案数也随之不同,不一定为 \(1\),如若 \(f_i\) 表示 \(i\) 个点的无向图个数,则 \(f_i=2^{\frac{n(n+1)}{2}}\)),\(\hat G(x)=exp(\hat F(x))\) 的 \(g_i\) 就表示将 \(i\) 个元素划分成若干个“集合”的方案数(这里的“集合”同上面 \(f_i\) 所表示的集合)
举个例子,设 \(f_i\) 表示 \(i\) 个点能构成的无向连通图个数,\(g_i\) 表示 \(i\) 个点能构成的无向图个数,并对于 \(f\) 和 \(g\) 设其对应的指数生成函数 \(\hat F(x)\) 和 \(\hat G(x)\),根据上面的组合意义,\(exp(\hat F(x))=\hat G(x)\)
解释一下上面那个式子的含义,根据 \(exp\) 的组合意义,对于无向连通图的生成函数求 \(exp\),此时上文第一段所说的“集合”在这里就是无向连通图的意思,而对于无向图,显然他可以由若干个小的无向连通图构成,所以说翻译第一段末尾的句子在此时的含义:\(g_i\) 表示将 \(i\) 个点划分为若干个无向连通图的方案数,那此时的 \(g_i\) 显然表示的就是无向图的个数
也可以这么理解,将 \(\hat F(x)\) 求 \(exp\) 后,即为从 \(\hat F(x)\) 所表示的所有集合中选取一些集合,让这些集合作为元素去构成一个新的大集合的方案数的生成函数(在上面的例子中 \(\hat F(x)\) 所表示的所有集合就是所有无向连通图,而求 \(exp\) 就是选一些无向连通图去构成一个新的大图,而这个大图就是无向图,也就是 \(\hat G(x)\))
形式化的来证明一下
设序列 \(f_i\ g_i\) 及其对应的指数生成函数 \(\hat F(x)\ \hat G(x)\),\(f_i\) 表示一个 \(i\) 个元素的“集合”的方案数,\(g_i\) 表示若干个“集合”且元素总个数为 \(i\) 的方案数
将第一段提到的等式列出:\(e^{\hat F(x)}=\hat G(x)\)
等式左边通过泰勒展开可以得出 \(e^{\hat F(x)}=\sum_{i=0}^{\infty}\frac{\hat F^i(x)}{i!}\) 也可以看成右边的 \(EGF\) 的封闭形式就是左边
考虑 \(EGF\) 乘法的组合意义,即为多重集排列,在这里 \(\hat F^i(x)\) 的组合意义便是用 \(i\) 个集合(其中元素有标号)组成一个大集合的方案数,\(\frac{1}{i!}\) 的组合意义便是由于集合之间是无序的,所以它是用来消序的,最后通过枚举集合的个数再求和即可算出若干小集合组成大集合的方案数,也就是等式右边
例题
- [集训队作业2013] 城市规划
- 有标号图计数,考虑指数生成函数,设 \(\hat F(x)\) 为无向连通图的指数生成函数,\(\hat G(x)\) 为无向图的生成函数
- 发现无向图就是若干个无向连通图,且他们之间无序,所以可以用 \(exp\) 的组合意义
- 列出等式:\(exp(\hat F(x))=G(x)\),同时取 \(ln\):\(\hat F(x)=ln\hat G(x)\)
- 集合划分计数
- 有标号计数,考虑 \(EGF\),划分为若干个集合且集合间无序,大集合划小集合,考虑 \(EGF\) 中 \(exp\) 的组合意义,小集合的 \(EGF\) 即为序列 \(<1,1,1,\dots>\) 的生成函数,\(exp\) 过后即为答案的生成函数
DGF
狄利克雷生成函数(\(dirichlet\ series\ generating\ function,DGF\)),常在数论函数中使用
函数 \(<f_1,f_2,f_3,\dots>\) 的 \(DGF\) 定义为 \(\tilde F(x)=\sum_{i=1}^{\infty}\frac{f_i}{i^x}\)
若函数 \(f\) 满足积性,即 \(\forall i\perp j,f_{ij}=f_if_j\),那么其 \(DGF\) 还可以表示为 \(\tilde F(x)=\prod_{p\in \mathcal{P}}\sum_{i=0}^{\infty}\frac{f_{p^i}}{p^{ix}}\),其中 \(\mathcal{P}\) 为质数集合,且默认 \(f_0=1\),证明可以考虑将累乘拆开,就是对于每一个 \(p\in \mathcal{P}\) 选一个 \(i\) 让 \(\frac{f_{p^i}}{p^{ix}}\) 成起来,由于 \(f\) 为积性函数,所以结果的分子就取遍 \(f\) 函数,而分母则是对应的 \(i^x\)
基本运算
两个函数 \(f,g\) 的 \(DGF\) 之积就是两者的狄利克雷卷积的 \(DGF\):
\(\tilde F(x)\tilde G(x)=\sum_{i=1}^{\infty}\sum_{j=1}^{\infty}\frac{f_ig_j}{(ij)^x}=\sum_{i=1}^{\infty}\frac{1}{i^x}\sum_{d|i}f_dg_{\frac{i}{d}}\)
这个等式的变换很好理解,就是从枚举 \(i,j\) 两个数变成枚举它俩的积 \(ij\) 以及积的因子,这种转化在数论函数问题中经常使用
常见积性函数的 \(DGF\)
黎曼函数
序列 \(<1,1,1,\dots>\) 的 \(DGF\) 为 \(\sum_{i=1}^{\infty}\frac{1}{i^x}=\zeta(x)\)
显然该序列满足积性,所以 \(\zeta(x)=\prod_{p\in \mathcal{P}}\sum_{i=0}^{\infty}\frac{1}{p^{ix}}=\prod_{p\in \mathcal{P}}\frac{1}{1-p^{-x}}\)
根据定义 \(\zeta(x-k)\) 即为序列 \(<1^k,2^k,3^k,\dots>\) 的 \(DGF\)
莫比乌斯函数
对于莫比乌斯函数 \(\mu\),它的 \(DGF\) 为 \(\tilde M(x)=\prod_{p\in \mathcal{P}}(1-\frac{1}{p^x})=\prod_{p\in \mathcal{P}}(1-p^{-x})\)
根据莫比乌斯反演得 \(\sum_{d|n}\mu(d)=[n=1]\),所以显然可得 \(\tilde M(x) \zeta(x)=1\)(等号右边为一个多项式,但是该多项式只有常数项),所以 \(\tilde M(x)=\frac{1}{\zeta(x)}\)
欧拉函数
对于欧拉函数 \(\varphi\),它的 \(DGF\) 为 \(\tilde\Phi(x) =\prod_{p\in \mathcal{P}}(1+\sum_{i=1}^{\infty}\frac{p^{i-1}(p-1)}{p^{ix}})=\prod_{p\in \mathcal{P}}(\frac{1-p^{-x}}{1-p^{1-x}})\)
所以有 \(\tilde\Phi(x)=\frac{\zeta(x-1)}{\zeta(x)}\)
幂函数
对于函数 \(I_k(n)=n^k\),它的 \(DGF\) 为 \(\prod_{p\in \mathcal{P}}\sum_{i=0}^{\infty}\frac{p^{ik}}{p^{ix}}=\prod_{p\in \mathcal{P}}\frac{1}{1-p^{k-x}}=\zeta(x-k)\)


 浙公网安备 33010602011771号
浙公网安备 33010602011771号