Python程序说明贝特朗悖论不是悖论

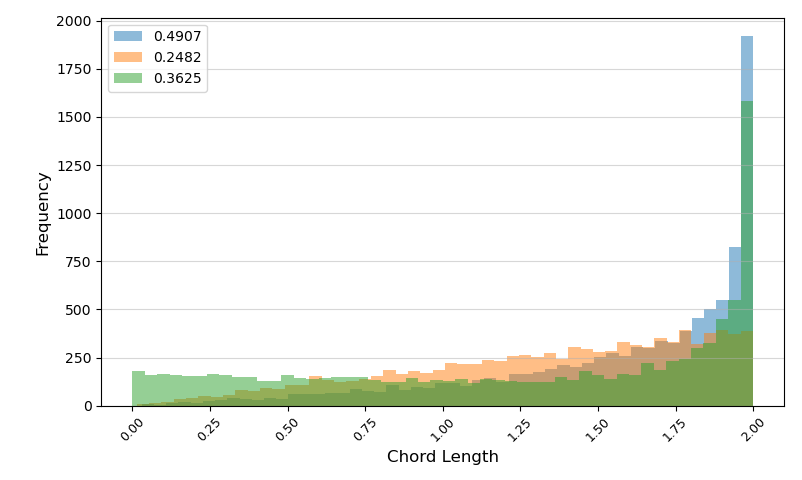
虽然三种方法得到的弦都能“覆盖”整个圆，但弦长的分布不同，见上图。

from math import pi
import numpy as np
from PIL import Image as Img, ImageDraw as ID
import matplotlib.pyplot as plt

R = 64 # 圆的半径r为1，放大为R
W = H = 2 * R + 16 # 图片比圆大一圈以免有些线画不全
N = 1_00_00 # 这么多次

# 圆心为原点，左上(-1, -1)，右下(1, 1)
# 输入为原始坐标, N * [x0, y0, x1, y1]
# 画图时左上(0, 0)，右下(W, H)
def line (draw, a) :
  a = R - a * R + 8 # a = W - (a + 1) * R - 8
  for i in range(N):
    draw.line( ((a[i,0],a[i,1]), (a[i,2],a[i,3])), fill=255 )

def do_it (i) :
  img = Img.new('L', (W, H)) # 单色'1'比灰度'L'慢
  draw = ID.Draw(img)

  # AI说连续多次rand是均匀分布
  y = np.random.uniform(low=-1.0, high=1.0, size=N)
  x = np.sqrt(1 - y ** 2)
  if i == 0: a = np.column_stack((-x, y, x, y))
  else: # signs别用两次！
    x *= np.random.choice([-1, 1], size=N)
    if i == 1:
      # (x,y)到(0,-1)
      a = np.column_stack((np.full_like(x, 0), np.full_like(y, -1),  x, y))
    else:
      y2 = np.random.uniform(low=-1.0, high=1.0, size=N)
      x2 = np.sqrt(1 - y2 ** 2) * np.random.choice([-1, 1], size=N)
      a = np.column_stack((x2, y2, x, y))

  line(draw, a); img.save(f'/t/{i}.png')

  # hypotenuse: 斜边
  a = np.hypot(a[:,2] - a[:,0], a[:,3] - a[:,1])
  prob = np.sum(a > 3 ** 0.5) / N # 概率
  # 弦覆盖圆吗？
  print(prob, (img.histogram()[255] / R ** 2) / pi)

  return a, str(prob)

for i in range(3):
  a,p = do_it(i); plt.hist(a, bins=50, alpha=0.5, label=p)

plt.xlabel('Chord Length', fontsize=12)
plt.ylabel('Frequency', fontsize=12)
plt.xticks(rotation=45, fontsize=9)
plt.grid(axis='y', alpha=0.5) # 显示网格
plt.tight_layout()
plt.legend()
plt.show()

“覆盖图”：

参考资料，中文搜“贝特朗悖论”即可，英文可Bing(PDF Bertrand paradox (probability) - Universitetet i Oslo).